原创:扣钉日记(微信公众号ID:codelogs),欢迎分享,转载请保留出处。
简介
众所周知,编程语言一般都内置了3种位运算符&(AND)、|(OR)、~(NOT),用来实现位运算,但其实还有一种非常常用的位运算,即异或^(XOR),数学中常用⊕表示。
异或的运算逻辑如下:
1 ⊕ 1 = 0
1 ⊕ 0 = 1
0 ⊕ 1 = 1
0 ⊕ 0 = 0
简单来说,异或的特性是,两个值相同,结果为0,不同则结果为1,所以才叫异或嘛,两个值相异再或起来,不就是1嘛
由于异或特殊的运算特性,使其可以实现一些神奇的操作,如下:
- 实现加减法
- 加解密
- 密钥交换
- 数据备份
那就来一起看看吧!
运算定律
任何值与自身异或,结果为0
x ^ x = 0任何值与0异或,结果为其自身
x ^ 0 = x交换律
x ^ y ^ z = x ^ z ^ y结合律
x ^ y ^ z = x ^ (y ^ z)异或的运算定律比较简单,就不写数学证明了,感兴趣可到网上搜索。
实现加减法
XOR的第一种运用场景就是实现加减法,在我们上小学时,应该都学过进位加法与退位减法来做加减运算,咱们来复习一下吧。
异或其实与这个类似,不过它不会产生进位与退位,如下:
- 如二进制加法
01 + 01 = 10,而异或运算是01 ^ 01 = 00,它其实做了加法,但高位不进位,所以异或又称不进位加法。 - 如二进制减法
10 - 01 = 01,而异或运算是10 ^ 01 = 11,也可以看做个位0向高位借了一个1当2来用,但高位不减1,所以异或也可以称为不退位减法。
利用异或的这个特性,只要再解决一下进位和退位问题,就可以实现加减法了,如下是java代码实现:
public static int intPlus(int a, int b){
while (b != 0){
// 加法(未考虑进位)
int sum = a ^ b;
// 进位值,二进制中1 + 1的场景才会进位,a & b只有两个都为1,结果才是1,左移一位,就是进位值了
int addition = (a & b) << 1;
// 赋值,下次循环将进位加到a里面来,直到进位等于0
a = sum;
b = addition;
}
return a;
}
public static int intSubtract(int a, int b){
while (b != 0){
// 减法(未考虑退位)
int sum = a ^ b;
// 退位值,二进制中0 - 1的场景才会退位,~a & b只有a=0,b=1,结果才是1,左移一位,就是退位值了
int abdication = (~a & b) << 1;
// 赋值,下次循环将退位再从a中减掉,直到退位等于0
a = sum;
b = abdication;
}
return a;
}这也是为什么CPU里面都是做位运算的逻辑门电路,却能实现数值计算
加解密
使用XOR可以实现简单的加解密,假如明文为plain,密钥为key,密文为secret,则:
// 加密
secret = plain ^ key
// 解密
plain = secret ^ key为什么一定能解密呢,如下:
secret ^ key
= (plain ^ key) ^ key // 代入加密表达式
= plain ^ (key ^ key) // 代入结合律
= plain ^ 0 // 任何值与自身异或等于0
= plain // 任何值与0异或等于自身java实现如下:
public static byte[] xorEncrypt(byte[] plain, byte[] key){
byte[] secret = new byte[plain.length];
for(int i = 0; i < plain.length; i++){
secret[i] = (byte) (plain[i] ^ key[i % key.length]);
}
return secret;
}
public static byte[] xorDecrypt(byte[] secret, byte[] key){
return xorEncrypt(secret, key);
}
public static void main(String[] args) {
byte[] plain = "hello xor".getBytes(StandardCharsets.UTF_8);
byte[] key = "1234".getBytes(StandardCharsets.UTF_8);
byte[] secret = xorEncrypt(plain, key);
byte[] plain2 = xorDecrypt(secret, key);
// 输出 plain:aGVsbG8geG9y,secret:WVdfWF4SS1tD, plain2:aGVsbG8geG9y
System.out.printf("plain:%s,secret:%s, plain2:%s", Base64.encode(plain), Base64.encode(secret),
Base64.encode(plain2));
}密钥交换
密钥交换就是通信双方需要将加密密钥发送给对方,但不让中间的信道监听者知道密钥是什么,而利用XOR就可以实现一种最简单的密钥交换方案,如下:
- 客户端生成一个随机密钥p,然后再使用自己的密钥k1对其XOR加密,将加密后的s1发送给服务端,即s1 = p ^ k1。
- 服务端再使用自己的密钥k2对s1做XOR加密,将加密后的s2回复给客户端,即s2 = s1 ^ k2。
- 客户端再使用自己的密钥k1对s2做XOR解密,将解密后的s3回复给服务端,即s3 = s2 ^ k1。
- 服务端再使用自己的密钥k2对s3做XOR解密,即s4 = s3 ^ k2,而按XOR的性质,s4会等于p,即客户端顺利将p发送给了服务端,且中间通信数据都是加密的。
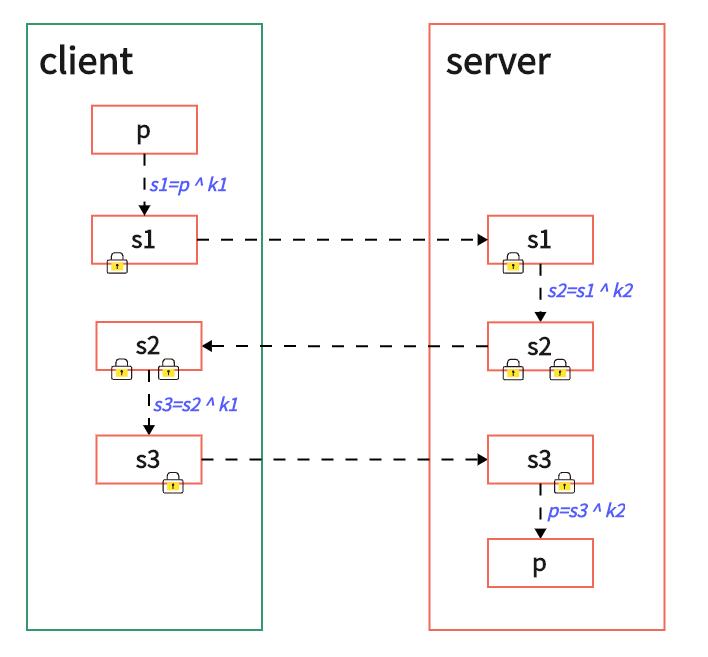
整个过程可以看做先是双方都在密文中做了一次加密,而后双方又逐步解开。
证明其正确性也很简单,只需要将式子代入一下即可,如下:
s4 = s3 ^ k2
= (s2 ^ k1) ^ k2
= ((s1 ^ k2) ^ k1) ^ k2
= (((p ^ k1) ^ k2) ^ k1) ^ k2
= p ^ k1 ^ k2 ^ k1 ^ k2 // 应用结合律
= p ^ (k1 ^ k2) ^ (k1 ^ k2) // 再应用结合律,把k1 ^ k2看成整体,就是加密之后再解密了
= p
//也可以这样证明
= p ^ k1 ^ k2 ^ k1 ^ k2
= p ^ (k1 ^ k1) ^ (k2 ^ k2) // 应用交换律
= p ^ 0 ^ 0 // 应用自身与自身异或为0
= p // 应用任何值与0异或为其自身数据备份
使用XOR也可以很容易实现多个数据的互备,如下:
假如有数据a、b、c,则z = a ^ b ^ c,然后把数据z备份下来。
- 当a丢失时,可使用
z ^ b ^ c来恢复。 - 当b丢失时,可使用
z ^ a ^ c来恢复。 - 当c丢失时,可使用
z ^ a ^ b来恢复。
这真是太神奇了,备份了一份数据z后,丢失了任何一份数据,都可以通过数据z与其它数据一起恢复回来,而磁盘阵列技术raid5的数据备份原理,就是用的这个特性。
实现异或
由于在布尔代数中,其实只需要与、或、非运算就可以实现所有其它运算,所以异或其实也是可以通过与、或、非实现的,最直观的实现方式如下:
a ^ b = (~a & b) | (a & ~b) ok,异或的使用场景就介绍到这了,还有没有其它神奇的运用场景呢?如果有,可留言告知下
往期内容
密码学入门
接口偶尔超时,竟又是JVM停顿的锅!
耗时几个月,终于找到了JVM停顿十几秒的原因
mysql的timestamp会存在时区问题?
真正理解可重复读事务隔离级别
字符编码解惑

