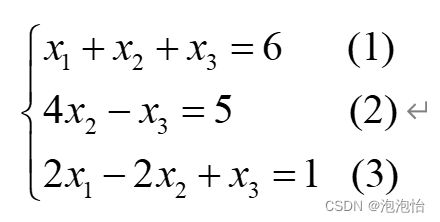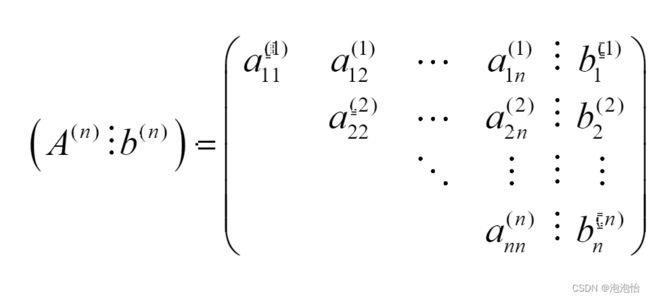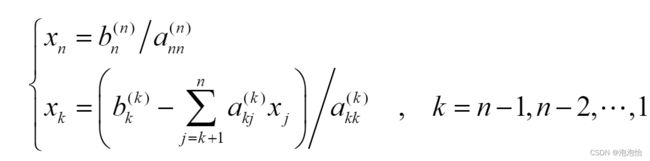高斯消元法解线性方程组数学原理及Python手工实现

一、基本思想

先逐次消去未知数，将方程化为同解的上三角形方程组，此过程称为消元。然后按方程相反顺序求解上三角形方程组，得到原方程组的解，此过程称为回代。这种方法称为高斯消元法。

二、例子

 消元过程如下：

 我们看式3我们可以求出x3=3,再依次向前面带入，便可求解x=[1,2,3]的转置。

三、推广一下：

这个线性方程组我们求解：

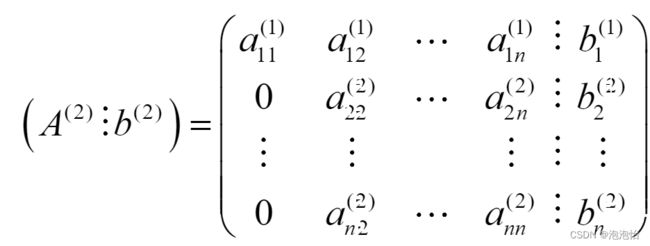
第一次消元：

 

 

 下面就是重复此步骤，很好理解，动笔写一下，就是如此简单

我们得进行n-1次消元最后得到：

 回代过程的公式：

在我进行编写代码的时候求xk我没有进行求和，而是直接矩阵运算，也可以求和，前提是你读入数据是DataFrame格式。

代码如下：

导包

import numpy as np
import sys

创建函数：

def SolveEq(A,b):
    if A.shape[0]!=A.shape[1]:
        print('系数矩阵不是方阵')
        sys.exit(0)
    n=A.shape[0]
    #消元
    for k in range(n-1):
        if A[k,k]<1e-8:
            print('主元素为零')
            sys.exit(0)
        for j in range(k+1,n):
            m=A[j,k]/A[k,k]
            A[j,k:n]= A[j,k:n]-m*A[k,k:n]
            b[j]=b[j]-m*b[k]
    #回代
    b[n-1]=b[n-1]/A[n-1,n-1]
    for i in range(n-2,-1,-1):
        b[i]=(b[i]-np.dot(A[i,i+1:n],b[i+1:n]))/A[i,i]
    return b

测试：

A=np.array([[1,1,1],[0,4,-1],[2,-2,1]])
b=np.array([[6],[5],[1]])
x= SolveEq(A,b)
x

结果：