强化学习（第二版）Sutton - 第二章习题答案和解析

强烈建议大家参考这位大佬的答案和解析，还有代码！！！

强化学习答案（第二版）

第二章

2.1

Q：在$ϵ$贪心动作选择中，在有两个动作及$ϵ=0.5$的情况下，贪心动作被选择的概率是多少？

A：0.5的概率选择开发（exploitation），选择贪心动作，0.5的概率选择试探（exploration），试探时有0.5的概率选择贪心动作，所有是$0.5+0.5\ast 0.5=0.75$

---

2.2

Q：赌博机的例子 考虑一个$k=4$的多臂赌博机问题，记做$1，2，3，4$。 将一个赌博机算法应用与这个问题，算法使用$ϵ-$贪心动作选择，基于采样平均的动作价值估计，初始估计为 $Q_1(a)=0,\forall a$。假设动作及收益的最初顺序是 $A_1=1，R_1=-1，A_2=2，R_2=1，A_3=2，R_3=-2，A_4=2，R_4=2，A_5=3，R_5=0$。在其中的某些案例中可能发生了$ϵ$的情形导致一个动作被随机选择。请回答，在哪些时刻中这种情形肯定发生了？在哪些时刻中这些情形可能发生了？

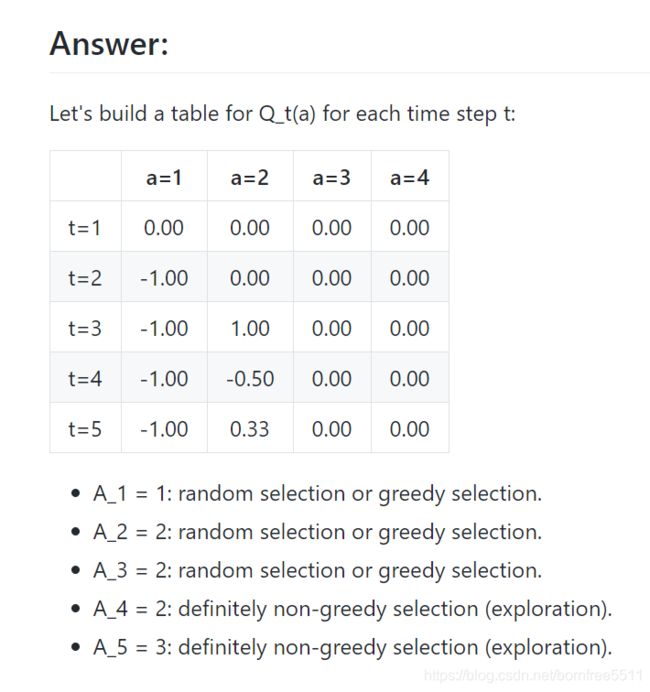
参考：https://github.com/borninfreedom/rlai-exercises/blob/master/Chapter%202/Exercise%202.2.md

---

2.3

Q：在图2.2所示的比较中，从累积收益和选择最佳动作的可能性的角度考虑，哪种方法会在长期表现最好？好多少？定量地表达你的答案。

A1：选择最优动作的概率是99.1%和91%，因为当进行试探的时候，也有可能选择最优的动作。 即$(1-0.01)+0.01\ast 1/10=99.1$ 和 $(1-0.1)+0.1\ast 1/10=91$.
(because there are 10-armed bandits, so there is a 1/10).
— answer from PiggyCh

A2:

---

2.4

---

2.6

Q：神秘的尖峰 图2.3中展示的结果应该是相当可靠的，因为他们是2000个独立随机的10臂赌博机任务的平均值。那么为什么乐观初始化方法在曲线的早期会出现振荡和峰值呢？换句话说，是什么使得这种方法在特定的早期步骤中表现的特别好或更糟？

A：在第10步训练步数之后的某点，智能体将会找到最优的动作值。它将会贪心的选择这个值。小的步长参数意味着对最优值的估计将会很慢的收敛到真值。看起来这个真值小于5。这意味着因为小的步长，次优的动作仍然会有一个接近于5的价值。因此，在某些点，智能体开始不断的选择次优动作。

---

2.7

---

2.8

Q：USB尖峰 在图2.4中，UCB算法的表现在第11步的时候有一个非常明显的尖峰。为什么会产生这个尖峰呢？请注意，你必须同时解释为什么收益在第11步时会增加，以及为什么在后续的若干步中会减少，你的答案才是令人满意的。提示如果$c=1$，那么这个尖峰就不会那么突出了

---

2.9

Q：证明在两种动作的情况下，softmax分布与通常在统计学和人工神经网络中使用的logistic或sigmoid函数给出的结果相同

---

2.10

2.5 & 2.11

#######################################################################
# Copyright (C)                                                       #
# 2016-2018 Shangtong Zhang([email protected])             #
# 2016 Tian Jun([email protected])                                #
# 2016 Artem Oboturov([email protected])                             #
# 2016 Kenta Shimada([email protected])                         #
# Permission given to modify the code as long as you keep this        #
# declaration at the top                                              #
#######################################################################

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
from tqdm import trange

matplotlib.use('Agg')


class Bandit:
    # @k_arm: # of arms
    # @epsilon: probability for exploration in epsilon-greedy algorithm
    # @initial: initial estimation for each action
    # @step_size: constant step size for updating estimations
    # @sample_averages: if True, use sample averages to update estimations instead of constant step size
    # @UCB_param: if not None, use UCB algorithm to select action
    # @gradient: if True, use gradient based bandit algorithm
    # @gradient_baseline: if True, use average reward as baseline for gradient based bandit algorithm
    def __init__(self, k_arm=10, epsilon=0., initial=0., step_size=0.1, sample_averages=False, UCB_param=None,
                 gradient=False, gradient_baseline=False, true_reward=0.):
        self.k = k_arm
        self.step_size = step_size
        self.sample_averages = sample_averages
        self.indices = np.arange(self.k)
        self.time = 0
        self.UCB_param = UCB_param
        self.gradient = gradient
        self.gradient_baseline = gradient_baseline
        self.average_reward = 0
        self.true_reward = true_reward
        self.epsilon = epsilon
        self.initial = initial

    def reset(self):
        # real reward for each action
        self.q_true = np.random.randn(self.k) + self.true_reward

        # estimation for each action
        self.q_estimation = np.zeros(self.k) + self.initial

        # # of chosen times for each action
        self.action_count = np.zeros(self.k)

        self.best_action = np.argmax(self.q_true)

        self.time = 0

    # get an action for this bandit
    def act(self):
        if np.random.rand() < self.epsilon:
            return np.random.choice(self.indices)

        if self.UCB_param is not None:
            UCB_estimation = self.q_estimation + \
                self.UCB_param * np.sqrt(np.log(self.time + 1) / (self.action_count + 1e-5))
            q_best = np.max(UCB_estimation)
            return np.random.choice(np.where(UCB_estimation == q_best)[0])

        if self.gradient:
            exp_est = np.exp(self.q_estimation)
            self.action_prob = exp_est / np.sum(exp_est)
            return np.random.choice(self.indices, p=self.action_prob)

        q_best = np.max(self.q_estimation)
        return np.random.choice(np.where(self.q_estimation == q_best)[0])

    # take an action, update estimation for this action
    def step(self, action):
        # generate the reward under N(real reward, 1)
        reward = np.random.randn() + self.q_true[action]
        self.time += 1
        self.action_count[action] += 1
        self.average_reward += (reward - self.average_reward) / self.time

        if self.sample_averages:
            # update estimation using sample averages
            self.q_estimation[action] += (reward - self.q_estimation[action]) / self.action_count[action]
        elif self.gradient:
            one_hot = np.zeros(self.k)
            one_hot[action] = 1
            if self.gradient_baseline:
                baseline = self.average_reward
            else:
                baseline = 0
            self.q_estimation += self.step_size * (reward - baseline) * (one_hot - self.action_prob)
        else:
            # update estimation with constant step size
            self.q_estimation[action] += self.step_size * (reward - self.q_estimation[action])
        return reward


def simulate(runs, time, bandits):
    rewards = np.zeros((len(bandits), runs, time))
    best_action_counts = np.zeros(rewards.shape)
    for i, bandit in enumerate(bandits):
        for r in trange(runs):
            bandit.reset()
            for t in range(time):
                action = bandit.act()
                reward = bandit.step(action)
                rewards[i, r, t] = reward
                if action == bandit.best_action:
                    best_action_counts[i, r, t] = 1
    mean_best_action_counts = best_action_counts.mean(axis=1)
    mean_rewards = rewards.mean(axis=1)
    return mean_best_action_counts, mean_rewards


def figure_2_1():
    plt.violinplot(dataset=np.random.randn(200, 10) + np.random.randn(10))
    plt.xlabel("Action")
    plt.ylabel("Reward distribution")
    plt.savefig('../images/figure_2_1.png')
    plt.close()


def figure_2_2(runs=2000, time=1000):
    epsilons = [0, 0.1, 0.01]
    bandits = [Bandit(epsilon=eps, sample_averages=True) for eps in epsilons]
    best_action_counts, rewards = simulate(runs, time, bandits)

    plt.figure(figsize=(10, 20))

    plt.subplot(2, 1, 1)
    for eps, rewards in zip(epsilons, rewards):
        plt.plot(rewards, label='epsilon = %.02f' % (eps))
    plt.xlabel('steps')
    plt.ylabel('average reward')
    plt.legend()

    plt.subplot(2, 1, 2)
    for eps, counts in zip(epsilons, best_action_counts):
        plt.plot(counts, label='epsilon = %.02f' % (eps))
    plt.xlabel('steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('../images/figure_2_2.png')
    plt.close()


def figure_2_3(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(epsilon=0, initial=5, step_size=0.1))
    bandits.append(Bandit(epsilon=0.1, initial=0, step_size=0.1))
    best_action_counts, _ = simulate(runs, time, bandits)

    plt.plot(best_action_counts[0], label='epsilon = 0, q = 5')
    plt.plot(best_action_counts[1], label='epsilon = 0.1, q = 0')
    plt.xlabel('Steps')
    plt.ylabel('% optimal action')
    plt.legend()

    plt.savefig('../images/figure_2_3.png')
    plt.close()


def figure_2_4(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(epsilon=0, UCB_param=2, sample_averages=True))
    bandits.append(Bandit(epsilon=0.1, sample_averages=True))
    _, average_rewards = simulate(runs, time, bandits)

    plt.plot(average_rewards[0], label='UCB c = 2')
    plt.plot(average_rewards[1], label='epsilon greedy epsilon = 0.1')
    plt.xlabel('Steps')
    plt.ylabel('Average reward')
    plt.legend()

    plt.savefig('../images/figure_2_4.png')
    plt.close()


def figure_2_5(runs=2000, time=1000):
    bandits = []
    bandits.append(Bandit(gradient=True, step_size=0.1, gradient_baseline=True, true_reward=4))
    bandits.append(Bandit(gradient=True, step_size=0.1, gradient_baseline=False, true_reward=4))
    bandits.append(Bandit(gradient=True, step_size=0.4, gradient_baseline=True, true_reward=4))
    bandits.append(Bandit(gradient=True, step_size=0.4, gradient_baseline=False, true_reward=4))
    best_action_counts, _ = simulate(runs, time, bandits)
    labels = ['alpha = 0.1, with baseline',
              'alpha = 0.1, without baseline',
              'alpha = 0.4, with baseline',
              'alpha = 0.4, without baseline']

    for i in range(len(bandits)):
        plt.plot(best_action_counts[i], label=labels[i])
    plt.xlabel('Steps')
    plt.ylabel('% Optimal action')
    plt.legend()

    plt.savefig('../images/figure_2_5.png')
    plt.close()


def figure_2_6(runs=2000, time=1000):
    labels = ['epsilon-greedy', 'gradient bandit',
              'UCB', 'optimistic initialization']
    generators = [lambda epsilon: Bandit(epsilon=epsilon, sample_averages=True),
                  lambda alpha: Bandit(gradient=True, step_size=alpha, gradient_baseline=True),
                  lambda coef: Bandit(epsilon=0, UCB_param=coef, sample_averages=True),
                  lambda initial: Bandit(epsilon=0, initial=initial, step_size=0.1)]
    parameters = [np.arange(-7, -1, dtype=np.float),
                  np.arange(-5, 2, dtype=np.float),
                  np.arange(-4, 3, dtype=np.float),
                  np.arange(-2, 3, dtype=np.float)]

    bandits = []
    for generator, parameter in zip(generators, parameters):
        for param in parameter:
            bandits.append(generator(pow(2, param)))

    _, average_rewards = simulate(runs, time, bandits)
    rewards = np.mean(average_rewards, axis=1)

    i = 0
    for label, parameter in zip(labels, parameters):
        l = len(parameter)
        plt.plot(parameter, rewards[i:i+l], label=label)
        i += l
    plt.xlabel('Parameter(2^x)')
    plt.ylabel('Average reward')
    plt.legend()

    plt.savefig('../images/figure_2_6.png')
    plt.close()


if __name__ == '__main__':
    figure_2_1()
    figure_2_2()
    figure_2_3()
    figure_2_4()
    figure_2_5()
    figure_2_6()

参考：

1. https://rs11.xyz/articles/38.html
2. https://1drv.ms/b/s!AtqFsO4cylhQgooFVAF1GZQuLOLsnA?e=zO3UmE
3. https://github.com/borninfreedom/reinforcement-learning-an-introduction/blob/master/chapter02/ten_armed_testbed.py