Diffusion扩散模型简述 + 代码demo
与GAN FLOW VAE类似扩散模型是一种生成模型。
需要用到的概率事实:
- 条件概率
- 马尔科夫链的转移公式
- 高斯分布的KL散度公式
K L ( P , Q ) = l o g σ 2 σ 1 + σ 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 − 1 2 ( 其 中 P . Q 为 一 维 高 斯 分 布 ) KL(P,Q)=log\frac{\sigma_2}{\sigma_1}+\frac{\sigma^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} -\frac12 { \tiny(其中P.Q为一维高斯分布)} KL(P,Q)=logσ1σ2+2σ22σ2+(μ1−μ2)2−21(其中P.Q为一维高斯分布) - 重参数技巧(从特殊高斯分布中采样点时不可导,将采样过程变为从标准分布N(0,1)采样的结果常量Z再用 μ \mu μ, σ \sigma σ变为目标高斯分布)
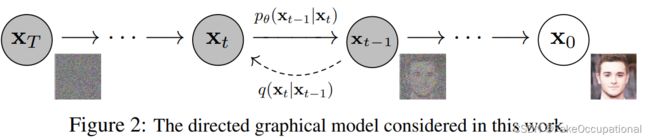
Diffusion
| 项目 | 描述 / p ( ⋅ ) p( \cdot ) p(⋅) |
|---|---|
| X T X_T XT | 各向同性的高斯分布 N ( X T ; 0 , I ) N(X_T;0,I) N(XT;0,I) |
| X 0 X_0 X0 | 训练数据集(的分布) |
- ⇐ \Leftarrow ⇐:扩散过程,逐渐添加高斯噪声,有序到无序,熵增过程
q ( x 1 : T ∣ x 0 ) : = Π t = 1 T q ( x t ∣ x t − 1 ) 其 中 q ( x t ∣ x t − 1 ) : = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_{1:T}|x_0):=\Pi_{t=1}^T q(x_t|x_{t-1}) \\ 其中q(x_t|x_{t-1}):=N(x_t;{\sqrt{1-\beta_t}x_{t-1}},\beta_t I) q(x1:T∣x0):=Πt=1Tq(xt∣xt−1)其中q(xt∣xt−1):=N(xt;1−βtxt−1,βtI)
β t ∈ ( 0 , 1 ) 可 以 如 参 考 文 献 33 设 置 为 冲 参 数 化 的 参 数 或 直 接 设 置 为 学 习 率 一 样 的 超 参 数 所 以 正 向 过 程 是 不 含 参 数 的 。 \tiny \beta_t \in (0,1)可以如参考文献33设置为冲参数化的参数或直接设置为学习率一样的超参数\\所以正向过程是不含参数的。 βt∈(0,1)可以如参考文献33设置为冲参数化的参数或直接设置为学习率一样的超参数所以正向过程是不含参数的。
扩散过程的一个显著特性是,它允许以闭合形式在任意时间步t对xt进行采样:
令 a t = 1 − β t ⇓ a ˉ t = Π s = 1 t a s q ( x t ∣ x 0 ) = N ( x t ; a ˉ t x 0 , ( 1 − a ˉ t ) I ) 令a_t = 1-\beta_t \Downarrow \bar a_t=\Pi_{s=1}^t a_s \\ q(x_t|x_0)=N(x_t;\sqrt{\bar a_t}x_0,(1-\bar a_t)I) 令at=1−βt⇓aˉt=Πs=1tasq(xt∣x0)=N(xt;aˉtx0,(1−aˉt)I)
上 式 的 推 导 过 程 : x t = a t x t − 1 + 1 − a t z t − 1 , 在 已 知 x t − 1 时 , 确 定 x t 的 高 斯 分 布 , 其 随 机 性 由 标 准 正 太 分 布 z t − 1 提 供 = a t ( a t − 1 x t − 2 + 1 − a t − 1 z t − 2 ) + 1 − a t z t − 1 因 为 需 要 通 过 马 尔 科 夫 链 获 取 x t 的 分 布 = a t a t − 1 x t − 2 + ( a t 1 − a t − 1 z t − 2 + 1 − a t z t − 1 ) 因 为 需 要 通 过 马 尔 科 夫 链 获 取 x t 的 分 布 = a t a t − 1 x t − 2 + ( a t 1 − a t − 1 ) 2 + ( 1 − a t ) 2 z 标 准 正 太 分 布 方 差 的 性 质 = a t a t − 1 x t − 2 + 1 − a t a t − 1 z ˉ t − 2 z ˉ 为 两 个 高 斯 分 布 的 混 合 = a ˉ t x 0 + 1 − a ˉ t z , 所 以 将 上 式 写 为 q ( x t ∣ x 0 ) = N ( x t ; a ˉ t x 0 , ( 1 − a ˉ t ) I ) 上式的推导过程:\\ \tiny x_t= \sqrt{a_t}x_{t-1} + \sqrt{1-a_t}z_{t-1} \ ,在已知x_{t-1}时,确定x_t的高斯分布,其随机性由标准正太分布z_{t-1}提供\\ \quad = \sqrt{a_t}(\sqrt{a_{t-1}}x_{t-2} + \sqrt{1-a_{t-1}}z_{t-2}) + \sqrt{1-a_t}z_{t-1} \ \ \ 因为需要通过马尔科夫链获取x_t的分布 \\ \quad = \sqrt{a_t}\sqrt{a_{t-1}}x_{t-2} +(\sqrt{a_t} \sqrt{1-a_{t-1}}z_{t-2} + \sqrt{1-a_t}z_{t-1} )\ \ \ 因为需要通过马尔科夫链获取x_t的分布 \\ \quad = \sqrt{a_t}\sqrt{a_{t-1}}x_{t-2} +\sqrt {(\sqrt{a_t} \sqrt{1-a_{t-1}})^2 +(\sqrt{1-a_t} )^2 }z \ \ \ 标准正太分布方差的性质 \\ \quad =\sqrt{a_t a_{t-1}}x_{t-2} +\sqrt{1-a_ta_{t-1}}\bar z_{t-2} \ \ \qquad \qquad \quad \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \bar z为两个高斯分布的混合 \\ =\sqrt{\bar{a}_t}x_0+\sqrt{1-\bar{a}_t}z,\quad \quad 所以将上式写为q(x_t|x_0)=N(x_t;\sqrt{\bar a_t}x_0,(1-\bar a_t)I) 上式的推导过程:xt=atxt−1+1−atzt−1 ,在已知xt−1时,确定xt的高斯分布,其随机性由标准正太分布zt−1提供=at(at−1xt−2+1−at−1zt−2)+1−atzt−1 因为需要通过马尔科夫链获取xt的分布=atat−1xt−2+(at1−at−1zt−2+1−atzt−1) 因为需要通过马尔科夫链获取xt的分布=atat−1xt−2+(at1−at−1)2+(1−at)2z 标准正太分布方差的性质=atat−1xt−2+1−atat−1zˉt−2 zˉ为两个高斯分布的混合=aˉtx0+1−aˉtz,所以将上式写为q(xt∣x0)=N(xt;aˉtx0,(1−aˉt)I)
unti-Diffusion
-
⇒ \Rightarrow ⇒:逆扩散过程(采样过程),无序到有序,熵减过程
联 合 分 布 p θ ( x 0 : T ) : = p ( x T ) Π t = 1 T p θ ( x t − 1 ∣ x t ) 其 中 p θ ( x t − 1 ∣ x t ) : = N ( x t − 1 ; μ θ ( x t , t ) , Σ θ ( x t , t ) ) , 即 假 设 p θ ( x t − 1 ∣ x t ) 也 为 高 斯 分 布 , 用 网 络 拟 合 其 中 的 系 数 μ θ ( x t , t ) , Σ θ ( x t , t ) 联合分布p_{\theta}(x_{0:T}):=p(x_T)\Pi_{t=1}^T \ p_{\theta}(x_{t-1}|x_t) \\ 其中p_{\theta}(x_{t-1}|x_t):= N{(x_{t-1};\mu_{\theta}(x_t,t) ,\Sigma_{\theta}(x_t,t))},\\ 即假设p_{\theta}(x_{t-1}|x_t)也为高斯分布,用网络拟合其中的系数\\ \mu_{\theta}(x_t,t) ,\Sigma_{\theta}(x_t,t) 联合分布pθ(x0:T):=p(xT)Πt=1T pθ(xt−1∣xt)其中pθ(xt−1∣xt):=N(xt−1;μθ(xt,t),Σθ(xt,t)),即假设pθ(xt−1∣xt)也为高斯分布,用网络拟合其中的系数μθ(xt,t),Σθ(xt,t) -
有了正向过程的分布,可以窥探逆向过程的分布,比如确定 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}| x_t,x_0) q(xt−1∣xt,x0)的标准差和均值
根 据 贝 叶 斯 定 理 转 换 P ( A ∣ B ) 和 P ( B ∣ A ) q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 . x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) 正 比 于 ∝ e x p ( − 1 2 ( ( x t − a t x t − 1 ) 2 β t + ( x t − 1 − a ‾ t − 1 x 0 ) 2 1 − a ˉ t − 1 − ( x t − a ‾ t x 0 ) 2 1 − a ˉ t ) ) = e x p ( − 1 2 ( ( a t β t + 1 1 − a ˉ t − 1 ) x t − 1 2 − ( 2 a t β t x t + 2 a ‾ t 1 − a ˉ t x 0 ) x t − 1 + C ( x t , x 0 ) ) ) 然 后 由 二 次 函 数 得 到 − 2 a b 得 到 均 值 , 和 方 差 得 到 方 差 β ˉ = 1 ( a t β t + 1 1 − a ˉ t − 1 ) = 1 − a ˉ t − 1 1 − a ˉ t ⋅ β t 均 值 u ˉ t ( x t , x 0 ) = ( a t β t x t + a ‾ t 1 − a t ˉ ) / ( α t β t + 1 1 − α ‾ t − 1 ) = a t ( 1 − a ‾ t − 1 ) 1 − a ˉ t x t + a ‾ t − 1 β t 1 − a ˉ t x 0 参 数 重 整 化 技 巧 ⇓ x t = = a ˉ t x 0 + 1 − a ˉ t z μ ˉ t = 1 a t ( x t − β t 1 − a ‾ t z t ) \tiny 根据贝叶斯定理 转换P(A|B) 和 P(B|A)\\ q(x_{t-1}| x_t,x_0) = q(x_t|x_{t-1}.x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ 正比于\propto exp(-\frac{1}{2}( \frac{(x_t-\sqrt{a_t}x_{t-1})^2}{\beta_t} + \frac{(x_{t-1}-\sqrt{\overline{a}_{t-1}}x_0)^2}{1-\bar{a}_{t-1}} -\frac{ (x_t - \sqrt{ \overline{a}_t}x_0)^2 }{1-\bar{a}_t} )) \\ = exp(-\frac{1}{2}( (\frac{a_t}{\beta_t }+\frac{1}{1-\bar a_{t-1}} )x_{t-1}^2 -(\frac{2\sqrt{a_t}}{\beta_t}x_t+\frac{2\sqrt{\overline a_t}}{1-\bar a_t}x_0)x_{t-1} +C(x_t,x_0) ))\\ 然后由二次函数得到-\frac{2a}{b}得到均值,和方差\\ 得到方差\bar \beta=\frac{1}{( \frac{a_t}{\beta_t }+\frac{1}{1-\bar a_{t-1}} )} = \frac{1-\bar a_{t-1}}{1-\bar a_t} \cdot \beta_t \\ 均值\bar{u}_t(x_t,x_0)=(\frac{\sqrt{a_t}}{\beta_t}x_t+\frac{\sqrt{\overline a_t}}{1-\bar{a_t}})/(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\overline{\alpha}_{t-1}}) \\ =\frac{\sqrt{a_t}(1-\overline{a}_{t-1})}{1-\bar{a}_{t}}x_t+\frac{\sqrt{\overline{a}_{t-1}\beta_t}}{1-\bar a_t}x_0 \\ 参数重整化技巧\Downarrow x_t==\sqrt{\bar{a}_t}x_0+\sqrt{1-\bar{a}_t}z \\ \bar \mu_t=\frac{1}{\sqrt{a_t}}(x_t - \frac{\beta_t}{\sqrt{1-\overline{a}_t}}z_t) 根据贝叶斯定理转换P(A∣B)和P(B∣A)q(xt−1∣xt,x0)=q(xt∣xt−1.x0)q(xt∣x0)q(xt−1∣x0)正比于∝exp(−21(βt(xt−atxt−1)2+1−aˉt−1(xt−1−at−1x0)2−1−aˉt(xt−atx0)2))=exp(−21((βtat+1−aˉt−11)xt−12−(βt2atxt+1−aˉt2atx0)xt−1+C(xt,x0)))然后由二次函数得到−b2a得到均值,和方差得到方差βˉ=(βtat+1−aˉt−11)1=1−aˉt1−aˉt−1⋅βt均值uˉt(xt,x0)=(βtatxt+1−atˉat)/(βtαt+1−αt−11)=1−aˉtat(1−at−1)xt+1−aˉtat−1βtx0参数重整化技巧⇓xt==aˉtx0+1−aˉtzμˉt=at1(xt−1−atβtzt)
- 差值称为漂移量
loss函数
− l o g p θ ( x 0 ) ≤ − l o g p θ ( x 0 ) + D K L ( q ( x 1 : T ∣ x 0 ) ∣ ∣ p θ ( x 1 : T ∣ x 0 ) ) D K L ≥ 0 = − l o g p θ ( x 0 ) + E x 1 : T ∼ q ( x 1 : T ∣ x 0 ) [ l o g q ( x 1 : T ∣ x 0 ) p θ ( x 1 : T ∣ x 0 ) ] K L 散 度 公 式 展 开 为 对 l o g q p 用 p 均 值 加 权 P 用 来 表 示 样 本 的 真 实 分 布 , q 用 来 表 示 模 型 所 预 测 的 分 布 = − l o g p θ ( x 0 ) + E x 1 : T ∼ q ( x 1 : T ∣ x 0 ) [ l o g q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) / p θ ( x 0 ) ] = − l o g p θ ( x 0 ) + E q [ l o g q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) / p θ ( x 0 ) + l o g p θ ( x 0 ) ] = − l o g p θ ( x 0 ) + E q [ l o g q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) / p θ ( x 0 ) ] + l o g p θ ( x 0 ) + l o g p θ ( x 0 ) 不 受 变 量 q 加 权 的 影 响 , 直 接 移 出 来 = E q [ l o g q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) / p θ ( x 0 ) ] 至 此 得 到 了 l o g 似 然 函 数 的 上 界 -log p_{\theta}(x_0) \leq -logp_{\theta}(x_0) + D_{KL}(q(x_{1:T}|x_0)|| p_{\theta}(x_{1:T}|x_0)) \ {\tiny \color{blue}D_{KL} \geq 0} \\ \quad = -log p_{\theta}(x_0) +E_{x1:T \sim q(x1:T |x_0)}[log\frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{1:T}|x_0)}] {\color{blue} \tiny KL散度公式展开为对log\frac{q}{p}用 p均值加权 P用来表示样本的真实分布,q用来表示模型所预测的分布} \\ \quad = -log p_{\theta}(x_0) +E_{x1:T \sim q(x1:T |x_0)}[log\frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{0:T})/p_{\theta}(x_0)}] \\ \quad = -log p_{\theta}(x_0) +E_{q}[log\frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{0:T})/p_{\theta}(x_0)}+logp_{\theta}(x_0)] \\ \quad = -log p_{\theta}(x_0) +E_{q}[log\frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{0:T})/p_{\theta}(x_0)}] +logp_{\theta}(x_0) {\color{blue} \tiny +logp_{\theta}(x_0) 不受变量q加权的影响,直接移出来}\\ \quad =E_{q}[log\frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{0:T})/p_{\theta}(x_0)}] {\color{blue} \tiny 至此得到了log似然函数的上界}\\ −logpθ(x0)≤−logpθ(x0)+DKL(q(x1:T∣x0)∣∣pθ(x1:T∣x0)) DKL≥0=−logpθ(x0)+Ex1:T∼q(x1:T∣x0)[logpθ(x1:T∣x0)q(x1:T∣x0)]KL散度公式展开为对logpq用p均值加权P用来表示样本的真实分布,q用来表示模型所预测的分布=−logpθ(x0)+Ex1:T∼q(x1:T∣x0)[logpθ(x0:T)/pθ(x0)q(x1:T∣x0)]=−logpθ(x0)+Eq[logpθ(x0:T)/pθ(x0)q(x1:T∣x0)+logpθ(x0)]=−logpθ(x0)+Eq[logpθ(x0:T)/pθ(x0)q(x1:T∣x0)]+logpθ(x0)+logpθ(x0)不受变量q加权的影响,直接移出来=Eq[logpθ(x0:T)/pθ(x0)q(x1:T∣x0)]至此得到了log似然函数的上界
然 后 将 − l o g p θ ( x 0 ) 写 成 交 叉 熵 的 形 式 L = E q ( x 0 ) [ − l o g p θ ( x 0 ) ] ≤ E q ( x 0 : T ) [ l o g q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] 将 刚 才 计 算 的 结 果 带 入 = E q ( x 0 : T ) [ l o g Π t = 1 T q ( x t ∣ x t − 1 ) p θ ( x T ) Π t = 1 T p θ ( x t − 1 ∣ x t ) ] 展 开 , 上 下 类 似 , 只 不 过 一 个 时 q 扩 散 , 一 个 是 p 逆 扩 散 = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 1 T l o g q ( x t ∣ x t − 1 ) p θ ( x t − 1 ∣ x t ) ] = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t ∣ x t − 1 ) p θ ( x t − 1 ∣ x t ) + l o g q ( x t ∣ x 0 ) p θ ( x 0 ∣ x t ) ] 取 出 其 中 的 一 项 q ( x t ∣ x t − 1 ) = q ( x t ∣ x t − 1 , x 0 ) ⇓ = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) p θ ( x t − 1 ∣ x t ) + l o g q ( x t ∣ x 0 ) p θ ( x 0 ∣ x t ) ] = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) ⋅ q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) + l o g q ( x t ∣ x 0 ) p θ ( x 0 ∣ x t ) ] = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + ∑ t = 2 T l o g q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) + l o g q ( x t ∣ x 0 ) p θ ( x 0 ∣ x t ) ] = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + l o g ( Π t = 2 T q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) ) + l o g q ( x t ∣ x 0 ) p θ ( x 0 ∣ x t ) ] = E q ( x 0 : T ) [ − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + l o g ( q ( x T ∣ x 0 ) q ( x 1 ∣ x 0 ) ) + l o g q ( x t ∣ x 0 ) p θ ( x 0 ∣ x t ) ] = E q ( x 0 : T ) [ l o g q ( x T ∣ x 0 ) − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + l o g ( − q ( x 1 ∣ x 0 ) ) ] = E q ( x 0 : T ) [ l o g q ( x T ∣ x 0 ) − l o g p θ ( x T ) + ∑ t = 2 T l o g q ( x t − 1 ∣ x t , x 0 ) p θ ( x t − 1 ∣ x t ) + l o g ( − q ( x 1 ∣ x 0 ) ) ] = E q [ D K L ( q ( x T ∣ x 0 ) ∣ ∣ p θ ( x T ) ) + ∑ t = 2 T D K L ( q ( x t − 1 ∣ x t , x 0 ) ∣ ∣ p θ ( x t − 1 ∣ x t ) ) + l o g ( − q ( x 1 ∣ x 0 ) ) ] ⇓ b l u e : 常 量 , r e d L t − 1 , b l a c k : L t − 1 且 t = 1 然后将-log p_{\theta}(x_0)写成交叉熵的形式 \\ L = E_{q(x_0)}[-log p_{\theta}(x_0)] \\ \leq E_{q(x_0:T)}[log\frac{q(x_{1:T}|x_0)}{p_{\theta}(x_{0:T})}] {\color{blue} \tiny 将刚才计算的结果带入} \\ = E_{q(x_0:T)}[log\frac{ \Pi_{t=1}^{T} q(x_t|x_{t-1}) }{ p_{\theta}(x_{T}) \Pi_{t=1}^{T} p_{\theta}(x_{t-1}|x_{t}) } ] {\color{blue} \tiny 展开,上下类似,只不过一个时q扩散,一个是p逆扩散}\\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=1}^T log\frac{ q(x_t|x_{t-1}) }{ p_{\theta}(x_{t-1}|x_{t}) } ] {\color{blue} \tiny } \\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=2}^T log\frac{ q(x_t|x_{t-1}) }{ p_{\theta}(x_{t-1}|x_{t}) } {\color{blue} \tiny }+ log\frac{ q(x_t|x_{0}) }{ p_{\theta}(x_{0}|x_{t}) } ] {\color{blue} \tiny 取出其中的一项 } \\ {\tiny q(x_t|x_{t-1})= q(x_t|x_{t-1},x_0) \Downarrow = \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{ q(x_{t-1}|x_0)} } \\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=2}^T log\frac{ \frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{ q(x_{t-1}|x_0)} }{ p_{\theta}(x_{t-1}|x_{t}) } {\color{blue} \tiny }+ log\frac{ q(x_t|x_{0}) }{ p_{\theta}(x_{0}|x_{t}) } ] {\color{blue} \tiny }\\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=2}^T log \frac{q(x_{t-1}|x_t,x_0)}{p_{\theta}(x_{t-1}|x_{t}) }\cdot \frac{q(x_t|x_0)}{ q(x_{t-1}|x_0)} {\color{blue} \tiny }+ log\frac{ q(x_t|x_{0}) }{ p_{\theta}(x_{0}|x_{t}) } ] {\color{blue} \tiny }\\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=2}^T log \frac{q(x_{t-1}|x_t,x_0)}{p_{\theta}(x_{t-1}|x_{t}) }+\sum_{t=2}^T log\frac{q(x_t|x_0)}{ q(x_{t-1}|x_0)} {\color{blue} \tiny }+ log\frac{ q(x_t|x_{0}) }{ p_{\theta}(x_{0}|x_{t}) } ] {\color{blue} \tiny }\\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=2}^T log \frac{q(x_{t-1}|x_t,x_0)}{p_{\theta}(x_{t-1}|x_{t}) }+log(\Pi_{t=2}^T \frac{q(x_t|x_0)}{ q(x_{t-1}|x_0)} ) {\color{blue} \tiny }+ log\frac{ q(x_t|x_{0}) }{ p_{\theta}(x_{0}|x_{t}) } ] {\color{blue} \tiny }\\ = E_{ q(x_0:T)}[ -log p_{\theta}(x_T)+\sum_{t=2}^T log \frac{q(x_{t-1}|x_t,x_0)}{p_{\theta}(x_{t-1}|x_{t}) }+log( \frac{q(x_T|x_0)}{ q(x_{1}|x_0)} ) {\color{blue} \tiny }+ log\frac{ q(x_t|x_{0}) }{ p_{\theta}(x_{0}|x_{t}) } ] {\color{blue} \tiny }\\ = E_{ q(x_0:T)}[ logq(x_T|x_0)-log p_{\theta}(x_T)+\sum_{t=2}^T log \frac{q(x_{t-1}|x_t,x_0)}{p_{\theta}(x_{t-1}|x_{t}) }+log( -{ q(x_{1}|x_0)} ) {\color{blue} \tiny } ] {\color{blue} \tiny }\\ = E_{ q(x_0:T)}[ {\color{blue}logq(x_T|x_0)-log p_{\theta}(x_T)}+ {\color{red}\sum_{t=2}^T log \frac{q(x_{t-1}|x_t,x_0)}{p_{\theta}(x_{t-1}|x_{t}) } }+log( -{ q(x_{1}|x_0)} ) {\color{blue} \tiny } ] {\color{blue} \tiny }\\ = E_{ q}[ {\color{blue}DKL(q(x_T|x_0)||p_{\theta}(x_T))}+ {\color{red}\sum_{t=2}^T DKL( {q(x_{t-1}|x_t,x_0)} || {p_{\theta}(x_{t-1}|x_{t}) } )}+log( -{ q(x_{1}|x_0)} ) {\color{blue} \tiny } ] {\color{blue} \tiny }\\ \\ \Downarrow \\ blue :\ 常量,red \ L_{t-1}, \ black :L_{t-1}且t=1 然后将−logpθ(x0)写成交叉熵的形式L=Eq(x0)[−logpθ(x0)]≤Eq(x0:T)[logpθ(x0:T)q(x1:T∣x0)]将刚才计算的结果带入=Eq(x0:T)[logpθ(xT)Πt=1Tpθ(xt−1∣xt)Πt=1Tq(xt∣xt−1)]展开,上下类似,只不过一个时q扩散,一个是p逆扩散=Eq(x0:T)[−logpθ(xT)+t=1∑Tlogpθ(xt−1∣xt)q(xt∣xt−1)]=Eq(x0:T)[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt∣xt−1)+logpθ(x0∣xt)q(xt∣x0)]取出其中的一项q(xt∣xt−1)=q(xt∣xt−1,x0)⇓=q(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0)=Eq(x0:T)[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣x0)q(xt−1∣xt,x0)q(xt∣x0)+logpθ(x0∣xt)q(xt∣x0)]=Eq(x0:T)[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)⋅q(xt−1∣x0)q(xt∣x0)+logpθ(x0∣xt)q(xt∣x0)]=Eq(x0:T)[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+t=2∑Tlogq(xt−1∣x0)q(xt∣x0)+logpθ(x0∣xt)q(xt∣x0)]=Eq(x0:T)[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+log(Πt=2Tq(xt−1∣x0)q(xt∣x0))+logpθ(x0∣xt)q(xt∣x0)]=Eq(x0:T)[−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+log(q(x1∣x0)q(xT∣x0))+logpθ(x0∣xt)q(xt∣x0)]=Eq(x0:T)[logq(xT∣x0)−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+log(−q(x1∣x0))]=Eq(x0:T)[logq(xT∣x0)−logpθ(xT)+t=2∑Tlogpθ(xt−1∣xt)q(xt−1∣xt,x0)+log(−q(x1∣x0))]=Eq[DKL(q(xT∣x0)∣∣pθ(xT))+t=2∑T DKL(q(xt−1∣xt,x0) ∣∣pθ(xt−1∣xt))+log(−q(x1∣x0))]⇓blue: 常量,red Lt−1, black:Lt−1且t=1
论 文 假 设 p θ ( x t − 1 ∣ x t ) 的 方 差 为 与 β 相 关 的 常 数 , 可 训 练 参 数 仅 有 均 值 , 主 要 关 注 红 色 部 分 论文假设p_{\theta}(x_{t-1}|x_{t})的方差为与\beta相关的常数,可训练参数仅有均值,主要关注红色部分 论文假设pθ(xt−1∣xt)的方差为与β相关的常数,可训练参数仅有均值,主要关注红色部分
⇓ K L ( P , Q ) = l o g σ 2 σ 1 + σ 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 − 1 2 ( 其 中 P . Q 为 一 维 高 斯 分 布 ) L t − 1 = E q [ ( μ 1 − μ 2 ) 2 2 σ t 2 ] L t − 1 = E q [ ( μ t ( x t , x o ) − μ θ ( x t , t ) ) 2 2 σ t 2 ] + C L t − 1 = E q [ ( μ t ( x t , x o ) − μ θ ( x t , t ) ) 2 2 σ t 2 ] + C 其 中 u ˉ t 逆 行 过 程 的 均 值 , 之 前 推 导 过 , \Downarrow KL(P,Q)=log\frac{\sigma_2}{\sigma_1}+\frac{\sigma^2+(\mu_1-\mu_2)^2}{2\sigma_2^2} -\frac12 { \tiny(其中P.Q为一维高斯分布)}\\ L_{t-1}=E_q[ \frac{(\mu_1-\mu_2)^2}{2\sigma_t^2} ]\\ L_{t-1}=E_q[ \frac{(\mu_t(x_t,x_o)-\mu_{\theta}(x_t,t))^2}{2\sigma_t^2} ]+C\\ L_{t-1}=E_q[ \frac{(\mu_t(x_t,x_o)-\mu_{\theta}(x_t,t))^2}{2\sigma_t^2} ]+C\\ 其中\bar u_t逆行过程的均值,之前推导过, ⇓KL(P,Q)=logσ1σ2+2σ22σ2+(μ1−μ2)2−21(其中P.Q为一维高斯分布)Lt−1=Eq[2σt2(μ1−μ2)2]Lt−1=Eq[2σt2(μt(xt,xo)−μθ(xt,t))2]+CLt−1=Eq[2σt2(μt(xt,xo)−μθ(xt,t))2]+C其中uˉt逆行过程的均值,之前推导过,
L ( θ ) : = E t , x 0 , ε [ ∣ ∣ ε − ε θ ( a ‾ t , + 1 − a ‾ t ε , t ) ) ∣ ∣ 2 ] L ( θ ) : = E t , x 0 , ε [ ∣ ∣ ε − m o d e l θ ( a ‾ t , ε , t ) ) ∣ ∣ 2 ] L(\theta):=E_{t,x_0,\varepsilon} [|| \varepsilon -\varepsilon_{\theta}(\sqrt{\overline a_t},+ \sqrt{1-\overline a_t }\varepsilon,t))||^2] \\ L(\theta):=E_{t,x_0,\varepsilon} [|| \varepsilon -model_{\theta}( \overline a_t,\varepsilon,t))||^2] L(θ):=Et,x0,ε[∣∣ε−εθ(at,+1−atε,t))∣∣2]L(θ):=Et,x0,ε[∣∣ε−modelθ(at,ε,t))∣∣2]
代码
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
import torch
# TODO 实验数据
s_curve , _ = make_s_curve(10**4 , noise = 0.1)
s_curve = s_curve[:,[0,2] ]/10.0
print("shape of moons :",np.shape(s_curve))
data = s_curve.T
fig,ax = plt.subplots()
ax.scatter(*data ,color='red',edgecolor='white')
ax.axis('off')
plt.show()
dataset = torch.Tensor(s_curve).float() # shape of moons : (10000, 2)
# TODO 确定超参数的值
num_steps = 100 # 可以由beta alpha 分布 均值 标准差 进行估算
# 学习的超参数 动态的在(0,1)之间逐渐增大
betas = torch.linspace(-6,6,num_steps)
betas = torch.sigmoid(betas)* (0.5e-2 - 1e-5) + 1e-5
# 计算 alpha , alpha_prod , alpha_prod_previous , alpha_bar_sqrt 等变量的值
alphas = 1 - betas
alphas_prod = torch.cumprod( alphas ,dim=0 ) # 累积连乘 https://pytorch.org/docs/stable/generated/torch.cumprod.html
alphas_prod_p = torch.cat([torch.tensor([1]).float() ,alphas_prod[:-1]],0) # p means previous
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1-alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1-alphas_prod)
assert alphas_prod.shape == alphas_prod.shape == alphas_prod_p.shape \
== alphas_bar_sqrt.shape == one_minus_alphas_bar_log.shape \
== one_minus_alphas_bar_sqrt.shape
print("all the same shape:",betas.shape) #
# TODO 确定扩散过程中任意时刻的采样值
def q_x(x_0 ,t):
noise = torch.randn_like(x_0) # noise 是从正太分布中生成的随机噪声
alphas_t = alphas_bar_sqrt[t] ## 均值 \sqrt{\bar \alpha_t}
alphas_l_m_t = one_minus_alphas_bar_sqrt[t] ## 标准差 \sqrt{ 1 - \bar \alpha_t}
# alphas_t = extract(alphas_bar_sqrt , t, x_0) # 得到sqrt(alphas_bar[t]) ,x_0的作用是传入shape
# alphas_l_m_t = extract(one_minus_alphas_bar_sqrt , t, x_0) # 得到sqrt(1-alphas_bart[t])
return (alphas_t * x_0 + alphas_l_m_t * noise)
# TODO 演示原始数据分布加噪100步后的效果
num_shows = 20
fig , axs = plt.subplots(2,10,figsize=(28,3))
plt.rc('text',color='blue')
# 共有10000个点,每个点包含两个坐标
# 生成100步以内每隔5步加噪声后的图像
for i in range(num_shows):
j = i // 10
k = i % 10
t = i*num_steps//num_shows # t=i*5
q_i = q_x(dataset ,torch.tensor( [t] )) # 使用刚才定义的扩散函数,生成t时刻的采样数据 x_0为dataset
axs[j,k].scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white')
axs[j,k].set_axis_off()
axs[j,k].set_title('$q(\mathbf{x}_{'+str(i*num_steps//num_shows)+'})$')
plt.show()
# TODO 编写拟合逆扩散过程 高斯分布 的模型
# \varepsilon_\theta(x_0,t)
import torch
import torch.nn as nn
class MLPDiffusion(nn.Module):
def __init__(self,n_steps,num_units=128):
super(MLPDiffusion,self).__init__()
self.linears = nn.ModuleList([
nn.Linear(2,num_units),
nn.ReLU(),
nn.Linear(num_units,num_units),
nn.ReLU(),
nn.Linear(num_units, num_units),
nn.ReLU(),
nn.Linear(num_units, 2),]
)
self.step_embeddings = nn.ModuleList([
nn.Embedding(n_steps,num_units),
nn.Embedding(n_steps, num_units),
nn.Embedding(n_steps, num_units)
])
def forward(self,x,t):
for idx,embedding_layer in enumerate(self.step_embeddings):
t_embedding = embedding_layer(t)
x = self.linears[2*idx](x)
x += t_embedding
x = self.linears[2*idx +1](x)
x = self.linears[-1](x)
return x
# TODO loss 使用最简单的 loss
def diffusion_loss_fn(model,x_0,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,n_steps):# n_steps 用于随机生成t
'''对任意时刻t进行采样计算loss'''
batch_size = x_0.shape[0]
# 随机采样一个时刻t,为了体检训练效率,需确保t不重复
# weights = torch.ones(n_steps).expand(batch_size,-1)
# t = torch.multinomial(weights,num_samples=1,replacement=False) # [barch_size, 1]
t = torch.randint(0,n_steps,size=(batch_size//2,)) # 先生成一半
t = torch.cat([t,n_steps-1-t],dim=0) # 【batchsize,1】
t = t.unsqueeze(-1)# batchsieze
# print(t.shape)
# x0的系数
a = alphas_bar_sqrt[t]
# 生成的随机噪音eps
e = torch.randn_like(x_0)
# eps的系数
aml = one_minus_alphas_bar_sqrt[t]
# 构造模型的输入
x = x_0* a + e *aml
# 送入模型,得到t时刻的随机噪声预测值
output = model(x,t.squeeze(-1))
# 与真实噪声一起计算误差,求平均值
return (e-output).square().mean()
# TODO 编写逆扩散采样函数(inference过程)
def p_sample_loop(model ,shape ,n_steps,betas ,one_minus_alphas_bar_sqrt):
'''从x[T]恢复x[T-1],x[T-2],……,x[0]'''
cur_x = torch.randn(shape)
x_seq = [cur_x]
for i in reversed(range(n_steps)):
cur_x = p_sample(model,cur_x, i ,betas,one_minus_alphas_bar_sqrt)
x_seq.append(cur_x)
return x_seq
def p_sample(model,x,t,betas,one_minus_alphas_bar_sqrt):
'''从x[T]采样时刻t的重构值'''
t = torch.tensor(t)
coeff = betas[t] / one_minus_alphas_bar_sqrt[t]
eps_theta = model(x,t)
mean = (1/(1-betas[t].sqrt()) * (x-(coeff * eps_theta)))
z = torch.randn_like(x)
sigma_t = betas[t].sqrt()
sample = mean + sigma_t * z
return (sample)
# TODO 模型的训练
seed = 1234
class EMA():
'''构建一个参数平滑器'''
def __init__(self,mu = 0.01):
self.mu =mu
self.shadow = {}
def register(self,name,val):
self.shadow[name] = val.clone()
def __call__(self, name, x): # call函数?
assert name in self.shadow
new_average = self.mu * x +(1.0 -self.mu) * self.shadow[name]
self.shadow[name] = new_average.clone()
return new_average
print('Training model ……')
'''
'''
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle = True)
num_epoch = 4000
plt.rc('text',color='blue')
model = MLPDiffusion(num_steps) # 输出维度是2 输入是x 和 step
optimizer = torch.optim.Adam(model.parameters(),lr = 1e-3)
for t in range(num_epoch):
for idx,batch_x in enumerate(dataloader):
loss = diffusion_loss_fn(model,batch_x,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,num_steps)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm(model.parameters(),1.) #
optimizer.step()
# for name ,param in model.named_parameters():
# if params.requires_grad:
# param.data = ems(name,param.data)
# print loss
if (t% 100 == 0):
print(loss)
x_seq = p_sample_loop(model,dataset.shape,num_steps,betas,one_minus_alphas_bar_sqrt)# 共有100个元素
fig ,axs = plt.subplots(1,10,figsize=(28,3))
for i in range(1,11):
cur_x = x_seq[i*10].detach()
axs[i-1].scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white');
axs[i-1].set_axis_off()
axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*10)+'})$')
参考与更多
2020 Denoising Diffusion Probabilistic Models
2015 Deep Unsupervised Learning using Nonequilibrium Thermodynamics
视频解读
DDPM的代码
https://github.com/openai/glide-text2im
基于扩散概率模型 (Diffusion Probabilistic Model ) 的音频生成模型
添加链接描述
https://www.jianshu.com/p/8b120d1881c1
(另辟蹊径—Denoising Diffusion Probabilistic 一种从噪音中剥离出图像/音频的模型)
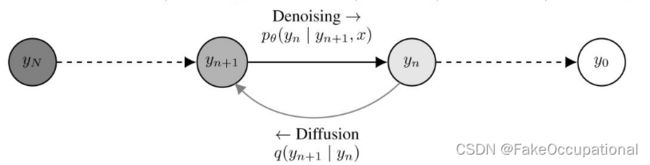

paper Diffusion Models Beat GANs on Image Synthesis
disco-diffusion
disco difussion repo:https://github.com/alembics/disco-diffusion
openai guided diffusion https://github.com/openai/guided-diffusion
在colab上运行的视频
github- docker - disco-diffusion
docker-本地运行版本
https://github.com/MohamadZeina/Disco_Diffusion_Local
实现中先使用了clip进行了连接文本和图像
https://github.com/afiaka87/clip-guided-diffusion