Pytorch 零基础学习系列 之 创建张量

Pytorch 零基础学习系列 之 创建张量

在深度学习中，神经网路结构是基础；在Pytorch中，张量是构建神经网络的基础 。从本质上讲，Pytorch就是一个处理张量的库。一个张量可以是一个数字、向量、矩阵或者任何n维数组。比较重要的一点是张量可以在GPU上进行计算。

例如，下图分别展示了1维张量，2维张量和3维张量：

如何创建一般张量？

方法一

(1) 导入 pytorch 和 numpy

import torch
import numpy as np

(2) 张量相关参数

torch.tensor(data, dtype = None, device = None, requires_grad = False, pin_memory = False)

其中，

• data：数据，可以是列表list，numpy的 ndarray
• dtype：数据类型，默认与data数据类型一致
• device：所在设备，GPU/CPU
• requires_grad：是否需要梯度，神经网路经常需要梯度
• pin_memory：是否存在锁页内存

(3) 使用numpy创建张量

通过 numpy 创建 ndarray，然后转化为张量，数据类型默认与 data一致。

arr = np.ones((3, 3))
print("数据类型：", arr.dtype)
t = torch.tensor(arr)
print(t)

运行结果：

数据类型： float64 tensor([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]], dtype=torch.float64)

如果在已经搭建了GPU环境运行，可以通过下面的代码在GPU 上创建张量（创建过程需要几秒的等待时间）

arr = np.ones((3, 3))
print("数据类型：", arr.dtype)
t = torch.tensor(arr, device = 'cuda')
print(t)

运行结果：

数据类型： float64 tensor([[1., 1., 1.], [1., 1., 1.], [1., 1., 1.]], device='cuda:0', dtype=torch.float64)

方法二

通过numpy创建的另外一种方法是：

使用 torch.from_numpy(ndarray)

这种方法只需要接受一个 ndarray 即可

arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)
print(arr)
print(t)

运行结果：

[[1 2 3] [4 5 6]] tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.int32)

注意

从torch.from_numpy 创建的 tensor 和 ndarray 共享内存，当修改其中一个的数据，另外一个也会被修改。

例如，在修改 array 的内容：

arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)

# 修改 array 的内容
arr[0,0] = 312
print(arr)
print(t)

运行结果：

[[312 2 3] [ 4 5 6]] tensor([[312, 2, 3], [ 4, 5, 6]], dtype=torch.int32)

再比如说，修改张量的内容：

arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)

# 修改 tensor 的内容
t[0,0] = -430
print(arr)
print(t)

运行结果：

[[-430 2 3] [ 4 5 6]] tensor([[-430, 2, 3], [ 4, 5, 6]], dtype=torch.int32)

创建全0张量

方法一

可以通过 torch.zeros() 创建全0张量

zeros(*size, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

其中，

• size：为张量形状
• out：输出的张量
• dtype：数据类型
• layout：内存中的布局形式，有strided，sparsed_coo等
• device：所在设备，GPU/CPU
• requires_grad：是否需要梯度，神经网路经常需要梯度

t1 = torch.tensor([1, 2, 3]) # 创建一个t1张量并赋初始值
t = torch.zeros((2,3), out = t1)
print(t, '\n', t1)
print(id(t), id(t1), id(t) == id(t1))

运行结果：

tensor([[0, 0, 0], [0, 0, 0]]) tensor([[0, 0, 0], [0, 0, 0]]) 2464000054400 2464000054400 True

通过上面显示的id发现，t和t1的id相同，所以t和t1在内存中指向的内存块相同。

方法二

可以通过torch.zeros_like() 创建全0张量：

torch.zeros(input, dtype = None, layout = None, device = None, requires_grad = False)

根据 input 形状创建全0张量

例如，创建一个 4*6 的全0张量

input = torch.empty(4, 6)
t = torch.zeros_like(input)
print(t)

运行结果：

tensor([[0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0.]])

创建全1张量

全1张量的创建和全0张量的创建方式基本一致，使用如下方式创建：

• torch.ones()
• torch.ones_like()

根据数值创建张量

方法一

• torch.full()

torch.full(size, fill_value, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

其中新出现的参数：

• fill_value：填充的值

例如，创建一个 2*2 的元素都是 8 的张量

t = torch.full((2, 2), 8 )
print(t)

运行结果：

tensor([[8, 8], [8, 8]])

方法二

torch.fuu_like()

torch.full_like(input, fill_value, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

例如，创建一个 4*3 的元素都为6的张量

input = torch.empty(4, 3)
t = torch.full_like(input, 6)
print(t) 

运行结果：

tensor([[6., 6., 6.], [6., 6., 6.], [6., 6., 6.], [6., 6., 6.]])

创建等差的一维张量

可以通过 torch.arange() 创建等差的一维张量

arange(start = 0, end, step = 1, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

其中，

• start：数列的起始值
• end： 数列的结束值，取不到的，只能取到 end - 1
• step：公差（步长），默认为1

t = torch.arange(1, 9, 2)
print(t)

运行结果：

tensor([1, 3, 5, 7])

创建等间距（均分）的一维张量

可以通过 torch.linspace() 来创建等间距均分张量

linspace(start, end, steps = 100, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

其中，

• steps：创建出的一维张量中元素个数
• end：结束位置可以取到

t = torch.linspace(1, 5, 4)
print(t)

运行结果：

tensor([1.0000, 2.3333, 3.6667, 5.0000])

注：linspace的图解

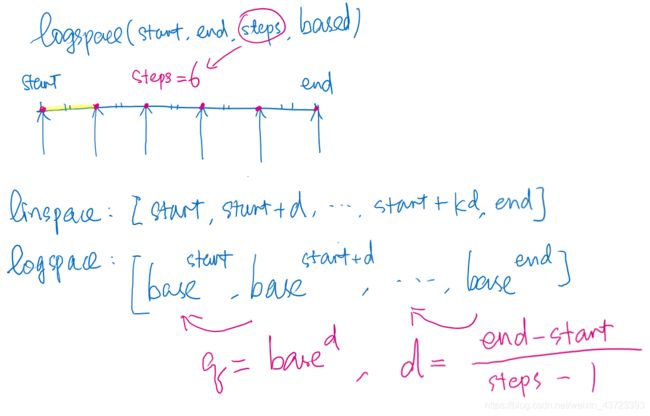
创建对数均分的一维张量

可以通过 torch.logspace() 来创建对数均分张量

logspace(start, end, steps = 100, base = 10.0, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

其中参数，

• base：对数函数的底，默认为10.0

t = torch.logspace(start = -5, end = 10, steps = 4)
print(t)

运行结果：

tensor([1.0000e-05, 1.0000e+00, 1.0000e+05, 1.0000e+10])

等间距均分 linspace 相当于 等差数列，对数均分 logspace 相当于 等比数列。对数均分相当于幂次的指数部分 成等间距均分。

t = torch.logspace(start = -2, end = 2, steps = 5, base = 2.0)
print(t)

tensor([0.2500, 0.5000, 1.0000, 2.0000, 4.0000])

注：logspace图解

创建单位对角矩阵（二维向量）

可以通过 torch.eye() 来创建单位对角矩阵。

torch.eye(n, m = None, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

其中，参数

• m：矩阵行数
• n：矩阵列数（默认为方阵）

t = torch.eye(4)
print(t)

运行结果：

tensor([[1., 0., 0., 0.], [0., 1., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 1.]])

创建正态分布（高斯分布）数据的张量

可以通过 torch.normal() 生成正态分布数据的张量

torch.noraml(mean, std, out = None)

其中，参数

• mean：均值
• std：标准差

这种正态分布的数据张量的创建方法可以分成4种方式：

(1) mean为张量，std为张量

(2) mean为标量，std为标量

(3) mean为标量，std为张量

(4) mean为张量，std为标量

（1）mean为张量，std为张量

# means为张量，std为张量
mean = torch.arange(1, 6, dtype = torch.float)
std = torch.arange(1, 6, dtype = torch.float)
t = torch.normal(mean, std)
print("mean:{}, std:{}".format(mean, std))
print(t)

运行结果：

mean:tensor([1., 2., 3., 4., 5.]), std:tensor([1., 2., 3., 4., 5.]) tensor([-0.9937, -0.4433, 5.5810, 6.5006, 0.1337])

此时，mean和std都是张量，可以理解为：

-0.9937是 mean = 1， std = 1 的正态分布采样得到，其他位置也是相应的正态分布采样得到，只是从不同的正态分布中采样罢了。

（2）mean为标量，std为标量

# mean为标量，std为标量
t = torch.normal(0.2, 1.0, size = (5, ))
print(t)

运行结果：

tensor([-0.6160, -0.6579, 0.5311, 0.2198, 0.4986])

这里生成的数据都是通过 mean = 0.2，std = 1.0 采样得到长度为5的一维张量。

（3） mean为标量，std为张量

# mean为标量，std为张量
mean = 2
std = torch.arange(1, 4, dtype = torch.float)
t = torch.normal(mean, std)
print("mean:{}, std:{}".format(mean, std))
print(t)

运行结果：

mean:2, std:tensor([1., 2., 3.]) tensor([ 1.2999, 2.6499, -3.2337])

1.2999是mean为2，std为1的正态分布采样得到，其他对应位置数据同理可得。只是从不同的正态分布中得到（均值相同，标准差不同）

（4）mean为张量，std为标量

# mean为张量，std为标量
mean = torch.arange(1, 4, dtype = torch.float)
std = 2
t = torch.normal(mean, std)
print("mean:{}, std:{}".format(mean, std))
print(t)

运行结果：

mean:tensor([1., 2., 3.]), std:2 tensor([-0.3166, 1.6594, 2.7413])

11.6594是mean为2，std为2的正态分布采样得到，其他对应位置数据同理可得。只是从不同的正态分布中得到（均值不同，标准差相同）

小结

(1) mean为张量，std为张量 —— 每次采样的正态分布均值不同，标准差也不同

(2) mean为标量，std为标量—— 每次采样的正态分布均值相同，标准差也相同

(3) mean为标量，std为张量—— 每次采样的正态分布均值相同，标准差不同

(4) mean为张量，std为标量—— 每次采样正态分布均值不同，标准差相同

创建标准正态分布数据的张量

一维标准正态分布

标准正态分布 $X\sim N(0,1)$ 均值为0，标准差为1

• torch.randn()

torch.randn(*size, out = None, dtype = None, layout = torch.strided, device = None, requires_grad = False)

size ：张量的形状

例如，创建一个长度为6的标准正态分布张量：

print(torch.randn(6))

运行结果：

tensor([-0.4437, 0.4294, 0.6771, -0.5297, -1.0764, -0.2395])

二维标准正态分布

print(torch.randn(3, 4))

运行结果：

tensor([[-0.2408, -0.3853, 0.8474, -1.4925], [ 0.4209, -0.2081, -0.7453, -0.4224], [ 0.0714, -0.6231, 0.2519, 1.3031]])

另一种办法

torch.randn_like() 可以根据张量的形状创建新的标准正态分布

randn_like(input, dtype = None, layout = None, device = None, requires_grad = False)

a = torch.ones((3,4))
t = torch.randn_like(a)
print(t)

运行结果：

tensor([[ 0.5477, -0.4851, 0.4772, -0.5393], [ 1.0461, 0.1628, 0.0659, 0.3142], [ 0.2300, 1.2297, 1.1029, -0.3967]])

创建在$(0,1]$上均匀分布的张量

一维均匀分布

• torch.rand()

torch.rand(*size, out = None, layout = torch.strided, device = None, requires_grad = False)

print(torch.rand(5))

tensor([0.4322, 0.7985, 0.9677, 0.5745, 0.8513])

二维均匀分布

print(torch.rand(3, 4))

tensor([[0.4246, 0.3925, 0.1754, 0.7080], [0.9186, 0.9058, 0.8131, 0.6348], [0.7383, 0.6523, 0.8786, 0.9258]])

整数均匀分布

一维

在区间上创建整数均匀分布数据的张量:

torch.randint() 和 torch.randint_like()

torch.randint(low = 0, high, size, out = None, layout = torch.strided, device = None, requires_grad = False)

在区间 [low, high) 上生成整数均匀分布数据的张量

例如，创建在 [2,6) 上均匀分布的整数张量，长度为4的一维张量：

print(torch.randint(2, 6, (4, )))

运行结果：

tensor([5, 5, 5, 4])

二维

例如，创建在 [0,9) 上均匀分布的整数张量，二维张量：

print(torch.randint(9, (3, 4)))

运行结果：

tensor([[6, 4, 3, 2], [1, 8, 8, 4], [7, 8, 4, 0]])

创建随机排列一维向量 0~n-1

• torch.randprem()

torch.randperm(n, out = None, dtype = torch.int64, layout = torch.strided, device = None, requires_grad = False)

print(torch.randperm(6))

运行结果：

tensor([4, 0, 1, 3, 5, 2])

创建伯努利分布的张量

torch.bernoulli：生成伯努利分布（0-1分布，两点分布）

torch.bernoulli(input, *, generator = None, out = None)

其中，

• input：概率值

例如，先创建一个张量a，作为之后的概率值输入：

a = torch.empty(3, 3).uniform_(0, 1)
print(a)

运行结果：

tensor([[0.0085, 0.1244, 0.0287], [0.5544, 0.6066, 0.9340], [0.9562, 0.2950, 0.6683]])

然后通过a来创建张量t

t = torch.bernoulli(a) #使用上面创建的概率值a创建伯努利分布
print(t)

运行结果：

tensor([[0., 0., 1.], [1., 1., 1.], [1., 1., 0.]])