ptorch学习笔记1-张量的创建

1.张量是什么？

0维张量就是标量只有大小没有方向。有大小和方向的向量就是一维张量，矩阵就是2维张量，我们接触到的rgb彩色图像实际就是一个三维张量，长宽和通道数。因此可以知道，张量是一个多维数组，是标量、向量和矩阵的高纬拓展。

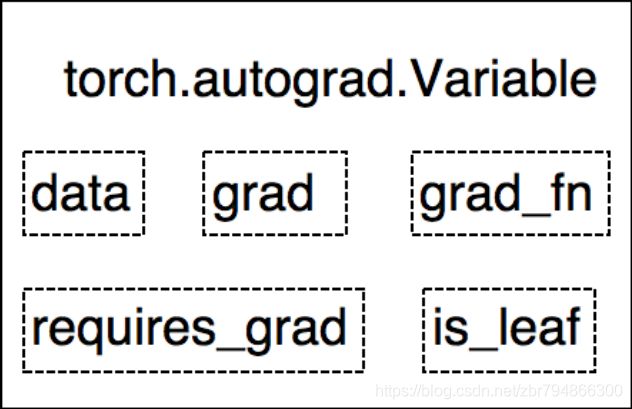
张量在pytorch中是以tensor表现出来。在pytorch0.40版本以前，自动求导的torch.autgrad.Variable是独立的，用来封装tensor，该数据类型主要有五个参数：

data: 被包装的 Tensor
grad: data 的梯度
grad_fn: 创建 Tensor 的 Function ,是自动
求导的关键
requires_grad: 指示是否需要梯度
is_leaf: 指示是否是叶子结点(张量)

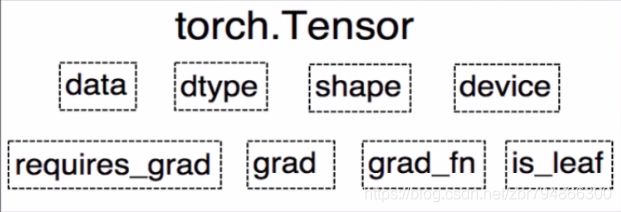
而在pytorch0.40以后的版本，为了方便，将vaiable数据类型并入到tensor。

在variable的基础之上多了三个部分：

dtype: 张量的数据类型,如 torch.FloatTensor, torch.cuda.FloatTensor
shape: 张量的形状,如 (64, 3, 224, 224)
device: 张量所在设备, GPU/CPU ,是加速的关键

2.张量的创建

创建张量有三种方法：一是直接创建法，二是依赖数值创建，三是依赖概率分布创建。

一.直接创建

1.torch.tensor

torch.tensor(
data,
dtype=None,
device=None,
requires_grad=False,
pin_memory=False)

功 能: 从data创建tensor
• data : 数据,可以是list,numpy
• dtype : 数 据 类 型 , 默认与 da ta 的 一致
• device : 所在设备,cuda /cpu
• requires_grad :是否需要梯度
• pin_memory : 是否存于锁页内存

# 通过torch.tensor创建张量

arr = np.ones((3,3))
print("ndarrary的数据集类型：", arr.dtype)
# t = torch.tensor(arr)
t = torch.tensor(arr, device='cuda')
print(t)

//运行结果:
ndarrary的数据集类型： float64
tensor([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]], device='cuda:0', dtype=torch.float64)

2.torch.form_numpy

功能:从 numpy 创建 tensor。注意事项:从 torch.from_numpy 创建的 tensor 于原 ndarray 共享内存,当修
改其中一个的数据,另外一个也将会被改动

arr = np.array([[1, 2, 3], [4, 5, 6]])
t = torch.from_numpy(arr)
print("numpy array", arr)
print("tensor: ", t)

print("\n修改 arr")
arr[0, 0] = 0
arr[1, 1] = 666
print("numpy array", arr)
print("tensor: ", t)

print("修改 tensor")
t[0, 0] = 555
t[1, 2] = 777
print("numpy array", arr)
print("tensor: ", t)

//运行结果：
umpy array [[1 2 3]
 [4 5 6]]
tensor:  tensor([[1, 2, 3],
        [4, 5, 6]])

修改 arr
numpy array [[  0   2   3]
 [  4 666   6]]
tensor:  tensor([[  0,   2,   3],
        [  4, 666,   6]])
修改 tensor
numpy array [[555   2   3]
 [  4 666 777]]
tensor:  tensor([[555,   2,   3],
        [  4, 666, 777]])

二.根据数值创建

1.torch.zeros()

根据size创建全0的张量。size张量的形状，如(3,3)、(3,255,255)。

torch.zeros(*size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

out_t = torch.tensor([1])
t = torch.zeros((3, 3), out=out_t)

print(out_t)
print(t, '\n', out_t)
print(id(t), id(out_t), id(t) == id(out_t))

//运行结果：
tensor([1])
tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]]) 
 tensor([[0, 0, 0],
        [0, 0, 0],
        [0, 0, 0]])
140275514982800 140275514982800 True

这里可以看出，输出的out和创建的张量out_t也是共地址的，一个改变，另一个一会改变

与zeros创建相同的还有torch.ones()用法和上述一样，创建的是size大小的全1张量。

与zeros和ones类似的还有torch.zeros_like()和torch.zeros_like()这两个是根据input的类型创建全0或者全1的张量

torch.zeros_like(input,    
dtype=None,
layout=None,
device=None,
requires_grad=False)

2.torch.full()

和zeros相似，根据size形状创建指定数据的张量。

torch.full(size,
fill_value,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

t = torch.full((4, 4), 6)
print(t)

//运行结果：
tensor([[6., 6., 6., 6.],
        [6., 6., 6., 6.],
        [6., 6., 6., 6.],
        [6., 6., 6., 6.]])

3.torch.arange()

创建等差的1为张量

torch.arange(start=0,
end,
step=1,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

数值区间start-end，顾头不顾尾，取不到end

start：数列的起始值，

end:结尾

step:公差，默认1

t = torch.arange(2, 8, 1)
print(t)

//运行结果
tensor([2, 3, 4, 5, 6, 7])

4.torch.linespace()

创建均分1维张量，数值区间为start-end 两头都能取到。

torch.linspace(start,
end,
steps=100,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

t = torch.linspace(2, 6, 3)
t1 = torch.linspace(2, 9, 4)
print(t, '\n', t1)

//运行结果：
tensor([2., 4., 6.]) 
 tensor([2.0000, 4.3333, 6.6667, 9.0000])

可以看到均分的步长=(end-start)/(step-1)

这里还有创建数均分的一维向量torch.logspace()。用的较少，有需要可以搜一下。

5.torch.eye()

创建单位对角矩阵，也就是2维的张量，这里默认是方阵，因此只需要一个参数n。

torch.eye(n,
m=None,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

t = torch.eye(4)
print(t)

//运行结果：
tensor([[1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 1., 0.],
        [0., 0., 0., 1.]])

三.根据概率分布创建张量

1.torch.normal()

生成正态分布（高斯分布）的张量

torch.normal(mean,
std,
out=None)

mean为均值，std维标准差,根据两者的标量和张量特性就有四种排列组合。

# mean：张量 std: 张量
mean = torch.arange(1, 5, dtype=torch.float)
std = torch.arange(1, 5, dtype=torch.float)
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)

# mean：标量 std: 标量
t_normal = torch.normal(0., 1., size=(4,))
print(t_normal)

# mean：张量 std: 标量
mean = torch.arange(1, 5, dtype=torch.float)
std = 1
t_normal = torch.normal(mean, std)
print("mean:{}\nstd:{}".format(mean, std))
print(t_normal)

//运行结果：
mean:tensor([1., 2., 3.])
std:tensor([1., 2., 3.])
tensor([1.6614, 2.5338, 3.1850])
tensor([ 0.6213, -0.4519, -0.1661, -1.5228])
mean:tensor([1., 2., 3.])
std:1
tensor([1.3817, 0.9724, 2.4369])

2.torch.rand()、torch.rand_like()、torch.randint()、torch.randint_like()

torch.rank()和torch.rand_like()是在区间[0,1)上生成随机分布

orch.rand(*size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

t = torch.rand(4, )
t1 = torch.rand((3, 3), )
print(t, '\n', t1)

//运行结果：
tensor([0.3259, 0.8550, 0.2891, 0.0947]) 
tensor([[0.7143, 0.2822, 0.6758],
        [0.3842, 0.7355, 0.9268],
        [0.2276, 0.1557, 0.9366]])

而torch.randint()、torch.randint_like()是在区间[low,high)内生成整数随机分布，其中size为张量的形状。

torch.randint(low=0,
high,
size,
out=None,
dtype=None,
layout=torch.strided,
device=None,
requires_grad=False)

t2 = torch.randint(5, (1, 4))
t3 = torch.randint(5, (3, 3))
print(t2, '\n', t3)


//运行结果
tensor([[2, 1, 0, 4]]) 
tensor([[3, 1, 3],
        [1, 2, 2],
        [3, 1, 0]])

3.torch.randperm()、torch.bernoulli()

torch.randperm()是生成从0--n-1的随机排列

n为张量的长度。

torch.randperm(n,
out=None,
dtype=torch.int64,
layout=torch.strided,
device=None,
requires_grad=False)

torch.bernoulli()伯努利分布以input为概率，生成0-1两点分布，需要注意的是，input必须为张量

torch.bernoulli(input,
*,
generator=None,
out=None)

t = torch.randperm(5)
print(t)

arr = torch.full((3, 3), 0.6)
t1 = torch.bernoulli(arr)
print(t1)

//运行结果：
tensor([1, 0, 3, 2, 4])
tensor([[0., 0., 1.],
        [1., 0., 0.],
        [1., 0., 0.]])

张量的创建的基本方法就如上所示。