一种改进的多元宇宙优化算法

一、理论基础

1、MVO算法

请参考这里。

2、IMVO算法

（1）非线性收敛因子

MVO算法中，算法寻优主要依靠黑洞基于虫洞进行穿越，在最优宇宙周围进行旅行，其旅行距离率$\text{TDR}$是协调算法探索能力和开发能力的重要变量，是影响基本MVO算法寻优的主要参数，但MVO算法中的$\text{TDR}$值由0.6凹型递减到0，其变化幅度过窄。较大的$\text{TDR}$值有利于全局探索能力，较小的$\text{TDR}$值有利于局部深度开发，在此，应该在迭代前期保持较快的迭代趋势进行全局探索，迭代后期保持较慢的迭代趋势，进行局部开发。因此，使用如下非线性收敛因子$$\text{TDR}=2\exp \left(-{\left(\frac{4l}{L}\right)}^2\right)\text{\hspace{1em}(1)}$$

（2）虫洞存在机制和白洞选择机制

基本MVO算法中，轮盘赌机制下的白洞多数是最优宇宙，从而没有很好地利用其它宇宙的信息，且虫洞存在概率由小到大，实验数据表明其概率大小对全局极值的获得并没有多大影响。因此，本文提出虫洞的固定存在机制为0.5，即每一轮迭代中，有一半宇宙都会利用虫洞进行穿越，在最优宇宙周围进行正负向随机搜索，定义穿越后的这些宇宙为白洞，剩余的宇宙为黑洞。

（3）黑洞围绕白洞公转

星团是宇宙中最大的引力结构，包含数百甚至数千个星系，它们被暗物质的大量晕圈所束缚，多元宇宙其实就是大量的星团结构。目前天文学家发现至少14个星系结构，而人类所处的是银河星系。银河星系中，包括大量的恒星、星团和星云，还有各种类型的星际气体和星际尘埃，银河系本身是一个旋转恒星，各种恒星围绕星系中心旋转，譬如地球围绕太阳公转，地球自身产生自转等。针对剩余的宇宙黑洞，定义它随机选定白洞星系进行螺旋式公转，从而解决种群间的代间信息沟通问题，黑洞的公转使用式(2)数学模型$$X^{\text{H}}(l+1)=\left|X^{\text{H}}(l)-X^{\text{B}}(l)\right|\cdot e^k\cdot \cos (2\pi k)\text{\hspace{1em}(2)}$$其中，$\text{H}$为宇宙黑洞，$\text{B}$为选定的宇宙白洞，$k$为$[-1,1]$之间的随机数。
基于上述策略，本文提出如下改进思想：宇宙膨胀时期，黑洞和白洞存在的机会均等，如果存在虫洞则黑洞穿越虫洞在最优宇宙周围进行以$\text{TDR}$旅行距离率进行探索成为白洞；如果不存在虫洞，则黑洞基于已经穿越的白洞进行螺旋式星系公转。

（4）IMVO算法流程

改进算法的实现流程描述如下：
步骤1 定义各参数：定义问题维度$D$、宇宙个数$N$、旅行距离率$\text{TDR}$，最大迭代步数$L$；
步骤2 初始化宇宙位置；
步骤3 迭代开始，计算各宇宙的膨胀化率(适应度)；
步骤4 白洞选择虫洞穿越：虫洞存在概率$\text{WEP}$为0.5，若$\text{WEP}>\text{Rand2}$，则存在虫洞，黑洞利用虫洞进行穿越，在最优宇宙周围旅行，按照式(3)更新位置$$X_j^{\text{H}}(l+1)=\{\begin{array}{l}{F}_j(l)-\text{TDR}(({\text{ub}}_j-{\text{lb}}_j)\text{rand}+{\text{lb}}_j),\text{Rand2}\ge 0.5\\ F_j(l)+\text{TDR}(({\text{ub}}_j-{\text{lb}}_j)\text{rand}+{\text{lb}}_j),\text{Rand2}<0.5\end{array}\text{\hspace{1em}(3)}$$其中，$F$为最优宇宙；
步骤5 黑洞围绕对应白洞公转：若$\text{WEP}<\text{Rand2}$，则不存在虫洞，剩余黑洞基于已穿越白洞宇宙进行公转，按照式(4)更新位置；$$X_j^{\text{H}}(l+1)=\left|X_j^{\text{H}}(l)-X_j^{\text{B}}(l+1)\right|\cdot e^k\cdot \cos (2\pi k)+X_j^{\text{B}}(l+1)\text{\hspace{1em}(4)}$$
步骤6 更新当前宇宙旅行距离率$\text{TDR}$。宇宙重新组合；
步骤7 循环结束条件判断，满足则结束，输出结果。不满足则跳转到步骤3。

二、仿真实验与结果分析

将IMVO与基本MVO进行对比，以常用23个测试函数中的F3、F4(单峰函数/10维)、F9、F10(多峰函数/10维)、F16、F17(固定维度多峰函数/2维、2维)为例，实验设置种群规模为30，最大迭代次数为500，每种算法独立运算30次，结果显示如下：

函数：F3
MVO：最差值: 0.20594, 最优值: 0.018511, 平均值: 0.079661, 标准差: 0.055409, 秩和检验: 3.0199e-11
IMVO：最差值: 1.2798e-10, 最优值: 5.0349e-22, 平均值: 7.205e-12, 标准差: 2.4187e-11, 秩和检验: 1
函数：F4
MVO：最差值: 0.14415, 最优值: 0.031376, 平均值: 0.088212, 标准差: 0.028312, 秩和检验: 3.0199e-11
IMVO：最差值: 4.003e-06, 最优值: 1.3425e-14, 平均值: 3.2996e-07, 标准差: 8.6881e-07, 秩和检验: 1
函数：F9
MVO：最差值: 32.8456, 最优值: 4.9834, 平均值: 17.3203, 标准差: 6.1205, 秩和检验: 4.111e-12
IMVO：最差值: 2.7697e-11, 最优值: 0, 平均值: 9.7108e-13, 标准差: 5.0512e-12, 秩和检验: 1
函数：F10
MVO：最差值: 2.0168, 最优值: 0.030909, 平均值: 0.21199, 标准差: 0.48702, 秩和检验: 3.0199e-11
IMVO：最差值: 1.0677e-06, 最优值: 2.4301e-11, 平均值: 7.1238e-08, 标准差: 2.3126e-07, 秩和检验: 1
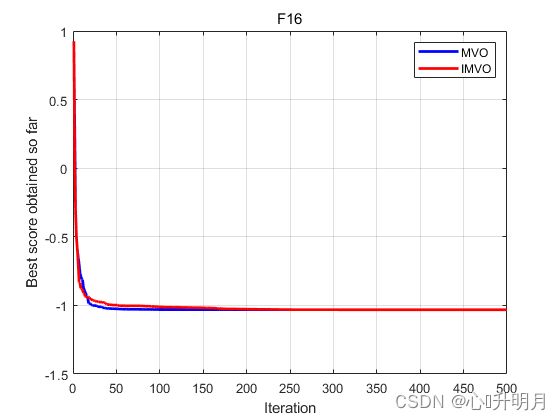
函数：F16
MVO：最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 3.7125e-07, 秩和检验: 3.0199e-11
IMVO：最差值: -1.0316, 最优值: -1.0316, 平均值: -1.0316, 标准差: 1.741e-13, 秩和检验: 1
函数：F17
MVO：最差值: 0.39789, 最优值: 0.39789, 平均值: 0.39789, 标准差: 7.4878e-07, 秩和检验: 3.018e-11
IMVO：最差值: 0.39789, 最优值: 0.39789, 平均值: 0.39789, 标准差: 2.9306e-13, 秩和检验: 1

实验结果表明：IMVO算法可以求解大规模实值优化问题，具有较强的鲁棒性和适用性。

三、参考文献

[1] 刘小龙. 改进多元宇宙算法求解大规模实值优化问题[J]. 电子与信息学报, 2019, 41(7): 1666-1673.