无人驾驶1:卡尔曼滤波原理及实现(以无人车观测为实例)
本系列文章,参考如下资料:
我真正理解卡尔曼滤波是看这篇文章,建议直接看原文:
1http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
对上文的翻译:
2.https://zhuanlan.zhihu.com/p/39912633
3.优达学城无人驾驶纳米课程
4.《概率机器人》Sebastian Trun, Wofram Burgard, Dieter Fox,机械工业出版社
5.《无人驾驶原理与实践》申泽邦 雍宾宾 周庆国 李良 李冠憬 机械工业出版社
1.数学背景知识
1.1 什么是高斯分布
高斯分布(Gaussian distribution):
也叫正态分布(Normal distribution),是一个在自然和社会科学中,非常广泛存在的一个连续概率分布。
概率密度函数为:
f ( x ) = 1 σ ( 2 π ) e − ( x − μ ) 2 2 σ 2 f(x) = \frac{1} {\sigma\sqrt{(2\pi)}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} f(x)=σ(2π)1e−2σ2(x−μ)2
如果把这个空间称为x, 那么高斯函数的性质可以用两个参数来反映,一个时均值 μ \mu μ,一个是宽度 σ 2 \sigma^2 σ2
1.2 高斯分布性质
σ 2 \sigma^2 σ2 反映曲线宽度, σ 2 \sigma^2 σ2 越大,曲线越宽,概率分布越分散,确定性越低,反之确定性越高。如下图所示
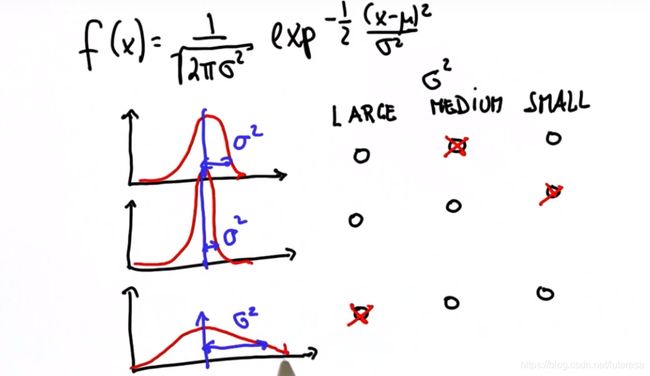
1.3 高斯分布计算
假设 μ \mu μ=10, σ 2 \sigma^2 σ2=4, 求x的概率?
from math import *
def gaussian(mu,sigma2,x):
return 1.0/sqrt(2.*pi*sigma2)*exp(-.5*(x-mu)**2/sigma2)
print(gaussian(10.,4.,8.))
print(gaussian(10.,4.,10.))
print(gaussian(10.,4.,12.))
在 Python 中计算曲线下方面积:
from scipy.stats import norm
def gaussian_probability(mean, stdev, x_low, x_high):
return norm(loc = mean, scale = stdev).cdf(x_high) - norm(loc = mean, scale = stdev).cdf(x_low)
1.4 高斯分布乘法
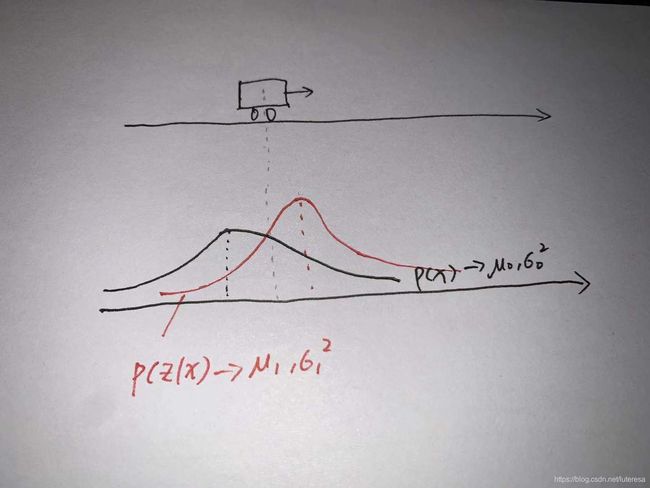
假设有如下场景,黑色曲线为一个车辆在一个维度上的初始概率分布(先验概率),蓝色曲线为当前场景一次测量的概率分布(条件概率)
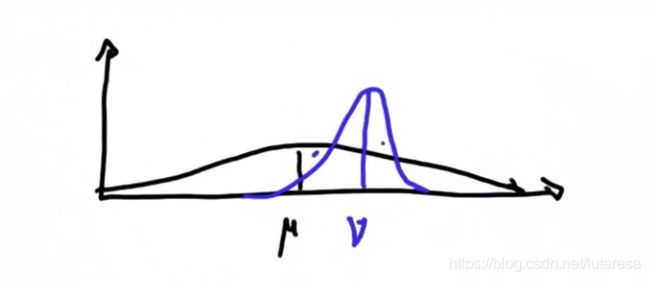
那么要计算当前车辆最佳估计,根据贝叶斯定理,后验概率=先验概率*条件概率

具体计算方法如下:
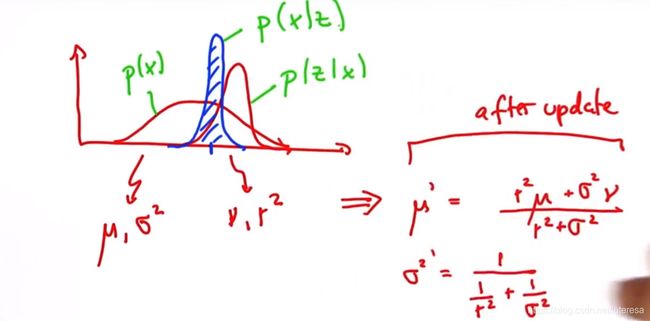
p(x): 先验概率
p(z|x): 测量更新
p(x|z): 后验概率
注:方差项不受均值影响,只使用之前的方差,得到一个更陡峭的方差;
代码实现:
# Write a program to update your mean and variance
# when given the mean and variance of your belief
# and the mean and variance of your measurement.
# This program will update the parameters of your
# belief function.
def update(mean1, var1, mean2, var2):
new_mean = (mean1*var2+mean2*var1)/(var1+var2)
new_var =1./(1./var1+1./var2)
return [new_mean, new_var]
例如: μ 1 \mu_1 μ1=10, σ 1 2 \sigma_1^2 σ12=4; μ 2 \mu_2 μ2=12, σ 2 2 \sigma_2^2 σ22=4;
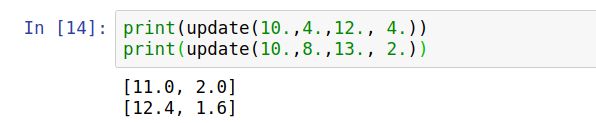

一个有点违反直觉的例子,假设有两个方差相同,均值不同的分布如下图,相乘结果如何:

结果是下图红色曲线表征的分布:

1.5 高斯分布加法
假设如下场景,一个车辆如下图蓝色曲线表征初始分布,然后移动u(移动量本身有误差,服从高斯分布),预计移动后分布时怎样?

计算方法:
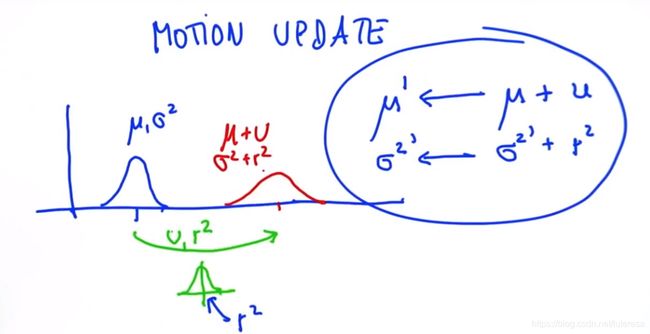
代码实现:
def predict(mean1, var1, mean2, var2):
new_mean = mean1 + mean2
new_var = var1 + var2
return [new_mean, new_var]
1.6多维高斯分布
实际应用中,需要观测的变量往往不只一个,设计多个维度,写成矩阵形式如下:

观测变量有D个组成一个D维向量, 不确定性用一个协方差矩阵表示
2. 卡尔曼滤波
2.1 什么是卡尔曼滤波
在物体跟踪、预测类的应用中,通常需要对目标状态进行状态估计预测。
因为在实际场景中通常需要持续观测、预测目标的运动和发展情况,以对当前状态采取更合适的决策。
而实际的传感器测量,由于测量的误差和噪声存在,测量值不完全可信。这时候,就可以采用概率学和统计学的方法来分析统计和估计状态量。
卡尔曼滤波就是这样一种结合预测(先验分布)和测量更新(似然估计)的状态估计算法。
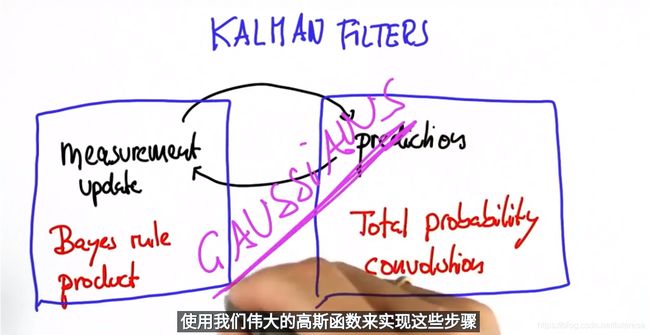
卡尔曼滤波总是包含两个大的部分,即测量更新和预测更新,下面通过实际案例来解释其原理;
2.2 一维卡尔曼滤波应用场景
假设有一辆汽车沿直线行驶,测量位置值有些许误差和干扰,应用卡尔曼滤波来提高定位的准确度。
step0 初始值: 假设汽车初始位置为( μ 0 \mu_0 μ0, σ 0 2 \sigma_0^2 σ02), 其概率分布为
g a u s s i a n 0 = g a u s s i a n ( μ 0 , σ 0 2 , x ) gaussian_0=gaussian(\mu_0,\sigma_0^2,x) gaussian0=gaussian(μ0,σ02,x)

step1 测量更新: 测量更新传感器测得汽车位置数据为( μ 1 \mu_1 μ1, σ 1 2 \sigma_1^2 σ12),即测量概率分布为
g a u s s i a n 1 = g a u s s i a n ( μ 1 , σ 1 2 , x ) gaussian_1=gaussian(\mu_1,\sigma_1^2,x) gaussian1=gaussian(μ1,σ12,x)
根据贝叶斯定律,测量后估计值修正为
g _ u p d a t e = g a u s s i a n 0 ∗ g a u s s i a n 1 g\_update = gaussian_0*gaussian_1 g_update=gaussian0∗gaussian1
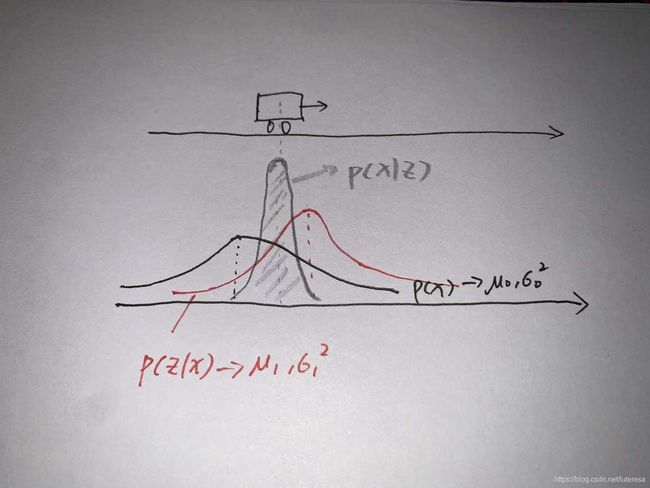
按1.4高斯乘法实现如下
def update(mean1, var1, mean2, var2):
new_mean = (mean1*var2+mean2*var1)/(var1+var2)
new_var =1./(1./var1+1./var2)
return [new_mean, new_var]
step2 预测更新:根据1.5高斯分布加法原理,实现如下
def predict(mean1, var1, mean2, var2):
new_mean = mean1 + mean2
new_var = var1 + var2
return [new_mean, new_var]
在实际持续运动过程中,会对step1/step2循环执行;一个具体案例实现如下:
measurements = [5., 6., 7., 9., 10.] #测量值
motion = [1., 1., 2., 1., 1.] #运动变化量
measurement_sig = 4. #测量高斯噪声
motion_sig = 2. #运动过程噪声
mu = 0.
sig = 10000. #车辆初始位置,sig=10000表示不确定性很高
# Write a program that will iteratively update and
# predict based on the location measurements
# and inferred motions shown below.
def update(mean1, var1, mean2, var2):
new_mean = float(var2 * mean1 + var1 * mean2) / (var1 + var2)
new_var = 1./(1./var1 + 1./var2)
return [new_mean, new_var]
def predict(mean1, var1, mean2, var2):
new_mean = mean1 + mean2
new_var = var1 + var2
return [new_mean, new_var]
# Insert code here
for i in range(len(measurements)):
mu,sig = update(mu,sig,measurements[i],measurement_sig) #测量更新,降低不确定性
print("update:", [mu, sig])
mu,sig = predict(mu,sig,motion[i],motion_sig) #预测更新,增大不确定性
print("predict:", [mu, sig])
print(mu, sig)
执行结果:

由上可知:每次执行update函数,不确定性降低;而执行完predict不确定性增大;
ps:
在任何含有不确定性信息的动态系统中,使用卡尔曼滤波,可以对下一步的趋势走向作出有根据的预测,即使总是伴随各种测量干扰和误差,卡尔曼滤波能指示出最接近真实发生的情况。
在连续变化的系统中,使用卡尔曼滤波效果非常理想,且它占用内存小(只保存前一个测量时刻的状态量,不需要保留其他历史数据),计算速度快,适合运用于解决实时问题和嵌入式系统。
2.3 多维卡尔曼滤波
1 多元高斯分布数学知识
协方差定义了分布的集中程度,如图,二维高斯分布图,分别表示三种不同相关性,沦落线某个分量上的范围,表示该向量的不确定性大小;
如果轮廓线是斜的,说明表示两个维度的不确定性是相关的;
2.卡尔曼滤波器可以估算隐藏变量

进行估算高维度空间时,当观测向量中有某些分量不容易测量时,可以根据其他测量值估算出来,这是卡尔曼滤波器在人工智能和控制理论方面,成为如此流行算法的原因之一。
下面实例解析其原理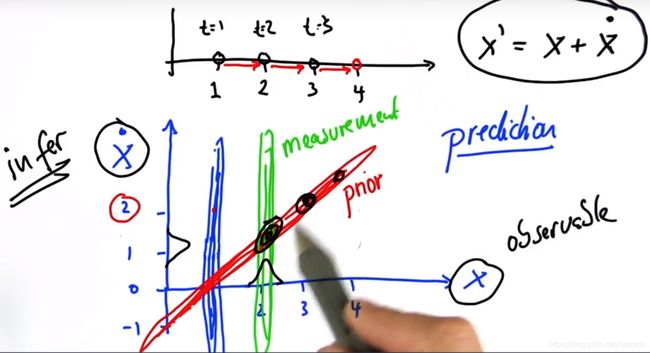
如图示,假设需要观测两个分量分别为位置和速度,但是传感器只能测量位置一个分量。
a.初始值,时刻t=1时观测到无人车位于1处,速度未知,所以此时二维高斯分布如图蓝色轮廓线所示;
b.当速度为0时,下一时刻位置依然为1;
当速度为1时,下一时刻位置为2,;
当速度为2时,下一时刻位置为3;
以此类推描绘出下一个时刻所有可能的分布,如上图红色轮廓线部分;
该分布单独投影到位置分量,得不到任何有效信息,单独投影到速度分量亦得不出有效信息,但是其反映了位置和速度的关联关系;
即当测量其中某一个值时(比如测量到位置为2时),由于速度未知,其分布如上图黄色部分描绘;
根据贝叶斯定理,可以得到该时刻的位置,速度二维高斯分布如上图黑色部分轮廓描绘;即可以估算出速度值;
3.完整卡尔曼滤波实现
step1:状态预测
x k ′ = a x k − 1 ′ + w k x_k^{'}=ax_{k-1}^{'} + w_k xk′=axk−1′+wk
a: 过程模型(Process Model), 常见为物理模型;
w k w_k wk:过程噪声(Process Noise),为简化计算,暂时忽略;
x k − 1 ′ x_{k-1}^{'} xk−1′:k-1时刻观测向量值;
step2:计算预测误差
p k ′ = a p k a T p_k^{'} = ap_ka^T pk′=apkaT
step3:计算卡尔曼增益
K k = p k ′ / ( p k ′ + r ) K_k = p_k^{'}/(p_k^{'}+r) Kk=pk′/(pk′+r)
K k K_k Kk: 表示卡尔曼增益
p k ′ p_k^{'} pk′:k时刻预测误差
r: 测量噪声,通常满足高斯分布(r, σ \sigma σ), r可以通过测量,或者直接从传感器厂商获得;
step4:计算最优估计值
X k ^ = x k ′ + K k ( z k − x k ′ ) \hat{X_k} = x_k^{'} + K_k(z_k-x_k^{'}) Xk^=xk′+Kk(zk−xk′)
X k ^ \hat{X_k} Xk^ : k时刻最优估计;
x k ′ : 过 程 模 型 计 算 的 k 时 刻 预 测 值 ; x_k^{'}: 过程模型计算的k时刻预测值; xk′:过程模型计算的k时刻预测值;
z k z_k zk: k时刻测量值;
上式可改写成
X k ^ = ( 1 − K k ) x k ′ + K k z k \hat{X_k} =(1-K_k) x_k^{'} + K_kz_k Xk^=(1−Kk)xk′+Kkzk
从这个公式可以看出,卡尔曼增益实际上就是一个权重,考虑极端情况
当 K k = 0 K_k=0 Kk=0, X k ^ = x k ′ \hat{X_k} =x_k^{'} Xk^=xk′: 表示当前测量极不可信,直接用预测值当作最优估算值;
当 K k = 1 K_k=1 Kk=1, X k ^ = z k ′ \hat{X_k} =z_k^{'} Xk^=zk′: 表示当前测量极其可信,直接用测量值当作最优估算值;
当 K k K_k Kk介于0~1之间,表示预测值和测量值都有可信度, 根据 K k K_k Kk所示权重取值;
step5:计算最优估计误差
p k = ( 1 − K k ) p k ′ p_k = (1-K_k)p_k^{'} pk=(1−Kk)pk′
p k p_k pk:k时刻最优估算值误差
注:该处 p k p_k pk用于下一个递推循环的预测更新;
用向量形式表示,对应公式如下图

注:公式不需要记忆,用时查询即可,重点是确定相关参数;
4.一个实例代码实现:
############################################
### use the code below to test your filter!
############################################
measurements = [1, 2, 3] #只能测量位置信号
#初始位置,速度值均为值,不确定性很高
x = matrix([[0.], [0.]]) # initial state (location and velocity)
P = matrix([[1000., 0.], [0., 1000.]]) # initial uncertainty
u = matrix([[0.], [0.]]) # external motion #
F = matrix([[1., 1.], [0, 1.]]) # next state function 状态转换函数
H = matrix([[1., 0.]]) # measurement function 只能测量位置
R = matrix([[1.]]) # measurement uncertainty 传感器噪声
I = matrix([[1., 0.], [0., 1.]]) # identity matrix
以上为相关参数及测量值,运用卡尔曼滤波求位置和速度的最佳估计
########################################
# Implement the filter function below
def kalman_filter(x, P):
for n in range(len(measurements)):
# measurement update
Z = matrix([[measurements[n]]])
print("z======================================")
print(Z)
y = Z - (H*x)
S = H*P*H.transpose() + R
K = P*H.transpose()*S.inverse()
x = x+(K*y)
P = (I-K*H)*P
# prediction
x = F*x + u
P = F*P*F.transpose()
print("x= ")
x.show()
print("p= ")
P.show()
print()
return x,P
执行结果如下
print(kalman_filter(x, P))

由结果知,估算出位置,速度分别为3.99, 0.99,实现过程用到的矩阵类如下:
# Write a function 'kalman_filter' that implements a multi-
# dimensional Kalman Filter for the example given
from math import *
class matrix:
# implements basic operations of a matrix class
def __init__(self, value):
self.value = value
self.dimx = len(value)
self.dimy = len(value[0])
if value == [[]]:
self.dimx = 0
def zero(self, dimx, dimy):
# check if valid dimensions
if dimx < 1 or dimy < 1:
raise ValueError("Invalid size of matrix")
else:
self.dimx = dimx
self.dimy = dimy
self.value = [[0 for row in range(dimy)] for col in range(dimx)]
def identity(self, dim):
# check if valid dimension
if dim < 1:
raise ValueError("Invalid size of matrix")
else:
self.dimx = dim
self.dimy = dim
self.value = [[0 for row in range(dim)] for col in range(dim)]
for i in range(dim):
self.value[i][i] = 1
def show(self):
for i in range(self.dimx):
print(self.value[i])
print(' ')
def __add__(self, other):
# check if correct dimensions
if self.dimx != other.dimx or self.dimy != other.dimy:
raise ValueError("Matrices must be of equal dimensions to add")
else:
# add if correct dimensions
res = matrix([[]])
res.zero(self.dimx, self.dimy)
for i in range(self.dimx):
for j in range(self.dimy):
res.value[i][j] = self.value[i][j] + other.value[i][j]
return res
def __sub__(self, other):
# check if correct dimensions
if self.dimx != other.dimx or self.dimy != other.dimy:
raise ValueError("Matrices must be of equal dimensions to subtract")
else:
# subtract if correct dimensions
res = matrix([[]])
res.zero(self.dimx, self.dimy)
for i in range(self.dimx):
for j in range(self.dimy):
res.value[i][j] = self.value[i][j] - other.value[i][j]
return res
def __mul__(self, other):
# check if correct dimensions
if self.dimy != other.dimx:
raise ValueError("Matrices must be m*n and n*p to multiply")
else:
# multiply if correct dimensions
res = matrix([[]])
res.zero(self.dimx, other.dimy)
for i in range(self.dimx):
for j in range(other.dimy):
for k in range(self.dimy):
res.value[i][j] += self.value[i][k] * other.value[k][j]
return res
def transpose(self):
# compute transpose
res = matrix([[]])
res.zero(self.dimy, self.dimx)
for i in range(self.dimx):
for j in range(self.dimy):
res.value[j][i] = self.value[i][j]
return res
# Thanks to Ernesto P. Adorio for use of Cholesky and CholeskyInverse functions
def Cholesky(self, ztol=1.0e-5):
# Computes the upper triangular Cholesky factorization of
# a positive definite matrix.
res = matrix([[]])
res.zero(self.dimx, self.dimx)
for i in range(self.dimx):
S = sum([(res.value[k][i])**2 for k in range(i)])
d = self.value[i][i] - S
if abs(d) < ztol:
res.value[i][i] = 0.0
else:
if d < 0.0:
raise ValueError("Matrix not positive-definite")
res.value[i][i] = sqrt(d)
for j in range(i+1, self.dimx):
S = sum([res.value[k][i] * res.value[k][j] for k in range(self.dimx)])
if abs(S) < ztol:
S = 0.0
try:
res.value[i][j] = (self.value[i][j] - S)/res.value[i][i]
except:
raise ValueError("Zero diagonal")
return res
def CholeskyInverse(self):
# Computes inverse of matrix given its Cholesky upper Triangular
# decomposition of matrix.
res = matrix([[]])
res.zero(self.dimx, self.dimx)
# Backward step for inverse.
for j in reversed(range(self.dimx)):
tjj = self.value[j][j]
S = sum([self.value[j][k]*res.value[j][k] for k in range(j+1, self.dimx)])
res.value[j][j] = 1.0/tjj**2 - S/tjj
for i in reversed(range(j)):
res.value[j][i] = res.value[i][j] = -sum([self.value[i][k]*res.value[k][j] for k in range(i+1, self.dimx)])/self.value[i][i]
return res
def inverse(self):
aux = self.Cholesky()
res = aux.CholeskyInverse()
return res
def __repr__(self):
return repr(self.value)
2.4.卡尔曼滤波算法为什么叫滤波算法?
以一维卡尔曼滤波为例,如果单纯的相信测量的信号,那么这个信号时包含噪声,很毛糙的,当运行卡尔曼滤波算法做估计时,估计的信号会很光滑,看起来似乎滤掉了噪声的影响,所以称之为卡尔曼滤波算法。
2.5 卡尔曼滤波优缺点
优点:在线性问题中被证明是最优估计。计算量小,占用内存小。
缺点:只能处理连续过程,线性系统。需人为给定系统模型,当系统模型不精确时,滤波效果会有所下降,但可以通过增加采样频率解决此问题。
建议应用场合:输入信号相对平稳或已知被测系统运动学模型,同时要求运算量极小的场合。



