机器学习数学基础之线代篇——线性代数python手册（建议收藏）

提到线性代数，又不得不吐槽国内教材了，学起来真的是实力劝退。有多少跟着国内教材学完线性代数课程后，知道线性代数是什么，它到底是干什么的？

事实上如果你后面想做科研、想研究机器学习、深度学习，你会发现处处是线性代数。这么抽象又重要的课程，一本书里基本看不到几张图，就好比是没有注释的代码，大概以为我的脑子就是记公式的机器吧…

如果你还未开始学习线性代数，那么强烈建议你把学校发的紫色教材放在一边，找几本国外的线性代数教材看看。然后在B站里搜一下麻省理工公开课Gilbert Strang老爷子的线性代数视频，相信你会打开新世界的大门（文末有彩蛋）——

---

吐槽就到这，我们先来看一个涉及线性代数本质问题的式子：
$$y=Ax$$
可以说，线性代数的很多问题都是从这个式子出发的。那么在线性代数中，如何理解这个式子呢？

直观上看，这个式子跟我们熟悉的一次函数 y = kx比较像。对于y=kx，我们可以理解为将标量x经过 某种线性变换，得到另一个标量y。

这里，我们把x和y换成向量，对于y = Ax，我们可以理解为将矩阵A（线性变换）作用于向量x ,得到另一个向量y。

由于向量就是空间中的一个点，这个种线性变换的作用就是将空间中的一个点变为空间中的另一个点。

对于函数y=kx，如果我们知道y和k，就能够求解出x。对于y=Ax也一样，如果y和A已知，我们同样可以求出x，这就是求解线性方程组的问题了。

其他知识点都是从这些基本的概念衍生出来的，这里就不一一列举了。任何新知识都不是凭空出来的，都是建立在以前的理论基础之上。在学习数学的时候，可以多联系以前的知识，类比着学习。

---

线性代数概念较多，计划在另一篇总结基本概念，这里仅总结线性代数里一些重要概念的python程序。

1 矩阵基本操作

注：向量操作与矩阵类似。

1.1 创建矩阵

（1）通过列表创建矩阵

#通过列表创建矩阵
import numpy as np
m = [[1,2,3],[4,5,6],[7,8,9]]  
a1 = np.array(m)
print("a1：",a1)
print("a1的大小：" ,a1.shape)
print("a1的类型：",type(a1))

（2）通过元组创建矩阵

#通过元组创建矩阵
t = ((1,2,3),(4,5,6),(7,8,9)) 
a2 = np.array(t)
print("a2：",t)
print("a2的大小：" ,a2.shape)
print("a2的类型：",type(a2))

（3）使用random()和randint()函数

random()函数随机生成矩阵中指定范围的浮点数：

import numpy as np
a1 = np.random.random((3,4))  #3×4阶，取值范围为0~1
print(a1)

randint()函数随机生成矩阵中指定范围的整数：

a2 = np.random.randint(1,10,size=[3,4])  #3×4阶，取值范围为1~10（不包括10）
print(a2)

1.2 改变矩阵的大小

import numpy as np
m = [1,2,3,4,5,6,7,8,9,10,11,12]
a = np.array(m)
a1 = a.reshape(3,4)
a2 = a.reshape(4,3)
print("原矩阵a: \n",a)
print("转换为3行4列矩阵a1:\n",a1)
print("转换为4行3列矩阵a2:\n",a2)

1.3 获取矩阵元素

print("a2的第0行元素a2[0]: \n",a2[0])
print("a2的前2行元素a2[0:2]: \n",a2[0:2])
print("a2的第0行和第2行元素a2[[0,2]]: \n",a2[[0,2]])
print("a2的第0列元素a2[:,1]: \n",a2[:,1])
print("a2的前2行元素a2[:,0:2]: \n",a2[:,0:2])
print("a2的第0列和第2列元素a2[:,[0,2]]: \n",a2[:,[0,2]])
print("a2的第2行第2列元素a2[2,2]: \n",a2[2,2])

1.4 特殊矩阵生成

（1）单位矩阵

import numpy as np
e1 = np.eye(5)
e2 = np.identity(5)
print("通过eye()创建五阶单位矩阵e1: \n",e1)
print("通过identity()创建五阶单位矩阵e2: \n",e2)

（2）零矩阵

import numpy as np
a = np.zeros((3,4))  
print("3×4阶零矩阵a: \n",a)

（3）对角矩阵

import numpy as np
m = [1,2,3,4,5]
a = np.diag(m)
print("创建对角线为1,2,3,4,5的对角矩阵： \n",a)

（4）上三角矩阵和下三角矩阵

import numpy as np
m = [[1,1,1,1],[2,2,2,2],[3,3,3,3],[4,4,4,4]]
a = np.array(m)
a1 = np.triu(a,0)
a2 = np.tril(a,0)
print("a矩阵：\n",a)
print("a矩阵的上三角矩阵： \n",a1)
print("a矩阵的下三角矩阵： \n",a2)

1.5 矩阵运算

（1）矩阵加减法运算

import numpy as np
m1 = [[1,1,1],[2,2,2]]
m2 = [[3,3,3],[4,4,4]]
a1 = np.array(m1)
a2 = np.array(m2)
print("a1 + a2 = \n",a1 + a2)
print("a1 - a2 = \n",a1 - a2)

（2）矩阵数乘运算

import numpy as np
m = [[5,5,5],[6,6,6]]
a = np.array(m)
print("矩阵数乘2a = \n",2*a)

（3）矩阵乘法运算

import numpy as np
a1 = np.array([[1,1,1],[2,2,2],[3,3,3]])
a2 = np.array([[4,4,4],[5,5,5],[6,6,6]])
a3 = np.dot(a1,a2)
a4 = a1.dot(a2)
a5 = a1*a2
a6 = np.multiply(a1,a2)
print("矩阵乘法a1×a2 = \n",a3)
print("矩阵乘法a1×a2 = \n",a4)
print("对应元素的乘积： \n",a5)
print("对应元素的乘积： \n",a6)

（4）矩阵乘方运算

import numpy as np
m = [[1,1,1],[2,2,2],[3,3,3]]
a = np.array(m)
a1 = a**2
print("a的二次方a1: \n",a1)

（5）生成逆矩阵

import numpy as np
m = [[2,5],[2,3]]
a = np.array(m)
a1 = np.linalg.inv(a)
a2 = np.mat(a)
a3 = a2.I
print("使用np.linalg.inv()求a的逆矩阵a1: \n",a1)
print("使用I属性求a的逆矩阵a3: \n",a3)

（6）生成转置矩阵

import numpy as np
m = [[1,2,3],[4,5,6]]
a = np.array(m)
a1 = a.T
a2 = np.transpose(a)
print("使用T属性求a的转置a1: \n",a1)
print("使用np.transpose()函数求a的转置a2: \n",a2)

2 行列式

2.1 行列式与矩阵的区别

（1）行列式是一个数值，矩阵是一个数表;

（2）行列式的行数等于列数，矩阵的行数不等于列数。

2.2 计算行列式

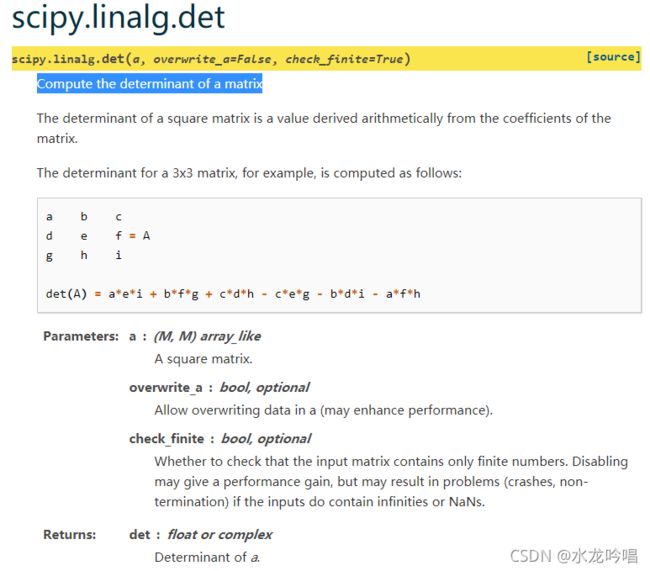
（1）使用np.linalg.det()函数计算行列式

官方手册用法：

python程序：

#计算行列式d
import numpy as np
d = [[1, 2, -4],[-2, 2, 1],[-3, 4, -2]]
a = np.array(d)
result = np.linalg.det(a)  
print(result)  #-14.000000000000004

（2）使用scipy.linalg.det()函数计算行列式

官方手册用法：

python程序：

# 计算行列式d
from scipy import linalg
d = [[1, 2, -4],[-2, 2, 1],[-3, 4, -2]]
a = np.array(d)
linalg.det(a)

2.3 计算矩阵的秩

使用np.linalg.matrix_rank() 函数计算矩阵的秩。

官方手册用法：

python程序：

# 计算矩阵d的秩
import numpy as np
m = [[2, -1, -1, 1, 2],[1, 1, -2, 1, 4],[4, -6, 2, -2, 4],[3, 6, -9, 7, 9]]
a = np.array(m)
rank = np.linalg.matrix_rank(m)
print(rank) #3

3 向量基本运算

3.1 向量的内积

python程序：

# 计算向量v1与向量v2的内积
import numpy as np
v1 = [[1,1,1]]
v2 = [[1,-2,1]]
a1 = np.array(v1).reshape(3,1)
a2 = np.array(v2).reshape(3,1)
result = a1.T.dot(a2)
print(result) #[[0]]

3.2 向量的长度

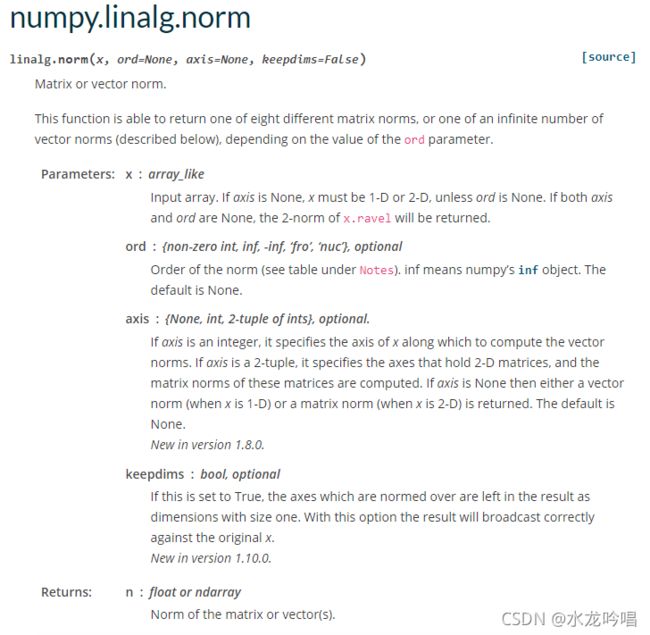
使用np.linalg.norm()函数：

官方手册用法：

python程序：

# 计算向量v的长度
import numpy as np 
v = [[1,2,2]]
a = np.array(v)
result =np.linalg.norm(a)
print(result) #3

4 计算线性方程组的解

（1）使用np.linalg.solve()函数

官方手册用法：

注意：这里系数矩阵必须是满秩，即所有行必须是线性无关的。

python程序：

#计算线性方程组的解
import numpy as np 
l1 = [[3, 2, -3],[2, -3, 3],[1, -1, 2]]
l2 = [[-2, 5, 5]]
a1 = np.array(l1)
a2 = np.array(l2).reshape(3,1)
result = np.linalg.solve(a1,a2)
print(result)

（2）使用scipy.linalg.solve()函数

官方手册用法（内容有点长）：

https://docs.scipy.org/doc/scipy/reference/reference/generated/scipy.linalg.solve.html#scipy.linalg.solve

python程序：

#计算线性方程组的解
from scipy import linalg
l1 = [[3, 2, -3],[2, -3, 3],[1, -1, 2]]
l2 = [[-2, 5, 5]]
a1 = np.array(l1)
a2 = np.array(l2).reshape(3,1)
result = linalg.solve(a1,a2)
print(result)

5 特征值与特征向量

5.1 计算特征值与特征向量

使用np.linalg.eig()函数：

官方手册用法：

python程序：

# 计算特征值和特征向量
import numpy as np
m = [[3,-1],[-1,3]]
a = np.array(m)
eig_val,eig_vex = np.linalg.eig(a)
print(eig_val) 
print(eig_vex) 

输出

特征值： 
 [4. 2.]
特征向量：
 [[ 0.70710678  0.70710678]
 [-0.70710678  0.70710678]]

5.2 特征值分解

特征值分解要求带分解的矩阵必须是n维方阵。

python程序：

import numpy as np
m1 = [[-2, 1, 1],[0, 2, 0],[-4, 1, 3]]  #m1为原始矩阵
a = np.array(m1)
eig_val,eig_vex = np.linalg.eig(a)
print("特征值为：",eig_val)
eig_val_diag = np.diag(eig_val) #特征值对角化
print("对角矩阵：",eig_val_diag)
m2 = eig_vex.dot(eig_val_diag.dot(np.linalg.inv(eig_vex))) #m2为新生成的矩阵
print(m2)
print("m1和m2是否相等：",np.allclose(m1,m2))

6 SVD

6.1 SVD要点

SVD（Singular Value Decompostion）可以对任意矩阵进行分解，它是一种抽取重要特征的方法，将一个复杂的大矩阵用三个小矩阵来表示，而这三个小矩阵包含大矩阵的重要特征信息。

6.2 使用SVD重构矩阵

python程序：

#奇异值分解
import numpy as np
m1 = [[1, 2, 2, 1],[2, 1, -2, -2],[1, -1, -4, -3]] # 原矩阵m1
a = np.array(m1)
u,s,vt = np.linalg.svd(a) 
diagma = np.zeros(np.shape(a))
diagma[:len(s),:len(s)] = np.diag(s)
print("左奇异值矩阵: \n",u) 
print("奇异值: \n",s)
print("右奇异值矩阵: \n",vt)
print("奇异值矩阵: \n",diagma)
m2 = u.dot(diagma.dot(vt)) # 重构后的矩阵m2
print("原矩阵m1与重构后矩阵m2是否相同：",np.allclose(m1,m2)) #判断重构后矩阵与原矩阵是否相等

输出：

左奇异值矩阵: 
 [[-0.34819307 -0.73853115  0.57735027]
 [ 0.4654902  -0.67080962 -0.57735027]
 [ 0.81368327  0.06772153  0.57735027]]
奇异值: 
 [6.38092733e+00 3.04692736e+00 1.50350788e-16]
右奇异值矩阵: 
 [[ 0.21885073 -0.16370335 -0.76510817 -0.58302235]
 [-0.66047812 -0.72715663 -0.13335703  0.13125468]
 [ 0.28819959 -0.02107189 -0.52371947  0.80138311]
 [-0.65788602  0.66633357 -0.35006188  0.02534264]]
奇异值矩阵: 
 [[6.38092733e+00 0.00000000e+00 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 3.04692736e+00 0.00000000e+00 0.00000000e+00]
 [0.00000000e+00 0.00000000e+00 1.50350788e-16 0.00000000e+00]]
原矩阵m1与重构后矩阵m2是否相同： True

6.3 使用SVD进行矩阵近似

for k in range(3,0,-1):
    m3 = u[:,:k].dot(diagma[:k,:k].dot(vt[:k,:]))
    print("k = ", k,"压缩后的矩阵： \n",np.round(m3,1))

6.4 使用SVD进行图像压缩

使用svd方法进行压缩有两种思路，一种是按照奇异值个数的百分比进行压缩，另一种是按照奇异值之和的百分比进行压缩。哪种方法比较好呢，我们来看一下执行结果。

python程序：

from PIL import Image
import numpy as np
import matplotlib.pyplot as plt

def svd1(data,percent):
    u,s,vt = np.linalg.svd(data) 
    diagma = np.zeros(np.shape(data))
    diagma[:len(s),:len(s)] = np.diag(s)  #获得奇异值矩阵
    num = (int)(percent*len(s))  #根据百分比得到奇异值的个数
    m = u[:,:num].dot(diagma[:num,:num].dot(vt[:num,:]))  #得到压缩后的矩阵
    return np.rint(m).astype("uint8")

def svd2(data,percent):
    print("svd2")
    u,s,vt = np.linalg.svd(data) 
    diagma = np.zeros(np.shape(data))
    diagma[:len(s),:len(s)] = np.diag(s)  #获得奇异值矩阵  
    percent_sum = (int)(sum(s)*percent)
    num = -1
    diagma_sum = 0
    while diagma_sum < percent_sum:
        num += 1
        diagma_sum += s[num]    
    m = u[:,:num].dot(diagma[:num,:num].dot(vt[:num,:]))  #得到压缩后的矩阵
    return np.rint(m).astype("uint8")

#重构图像
def rebuild(filename,percent,svd):
    img = Image.open(filename,'r')  #打开图片文件
    a = np.array(img) 
   
	#由于SVD输入的是单通道，RGB图像需要分解三个通道最后合并
	r = a[:, :, 0] 
    g = a[:, :, 1]
    b = a[:, :, 2]
    
    r_svd = svd(r,percent) 
    g_svd = svd(g,percent)
    b_svd = svd(b,percent)
    
    I=np.stack((r_svd,g_svd,b_svd),2)
    
    plt.figure(figsize=(20,20))    #指定单张图片大小
    plt.subplot(510 +(int)(percent*10/2))  #将子图划分为5行1列
    plt.title((int)(percent*10)) 
    plt.imshow(I)
    plt.show
    
filename = "E:\Tensorflow\code\cat\cat2.jpg"
for i in np.arange(0.2,1.2,0.2):
    rebuild(filename,i,svd1)
for i in np.arange(0.2,1.2,0.2):
    rebuild(filename,i,svd2)    

原图像：

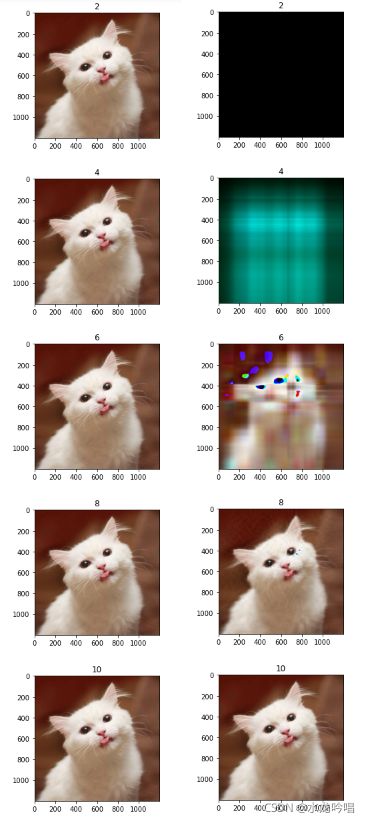
执行结果：

左边一列是使用svd1()方式进行压缩，分别对应取奇异值个数的20%、40%、60%、80%、100%进行压缩。从结果可以看出，即便是取20%的奇异值，与原图像基本无异。

右边一列是使用svd2()方式进行压缩，分别对应取奇异值之和的20%、40%、60%、80%、100%进行压缩，emm…前面三张压缩的结果就比较诡异了。最终按照奇异值之和的80%进行压缩，才能达到与原图像差不多的效果。

因此选择第一种，按奇异值个数进行压缩效果会比较好。

最后推荐一个，沉浸式学习线性代数网站——

http://immersivemath.com/ila/index.html

还有一本线性代数科普书，《程序员的数学：线性代数》，书都给你们找好了~

链接：https://pan.baidu.com/s/1I0dVisFjD8Uo-5DnFlJXrA
提取码：4tuk