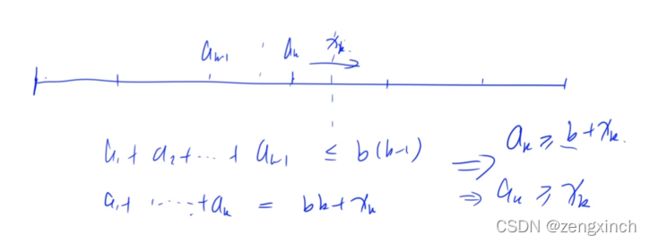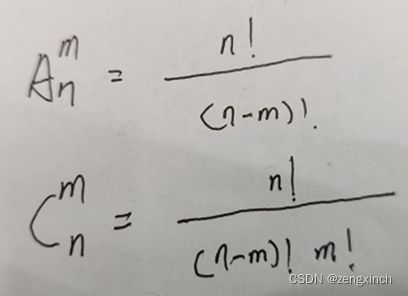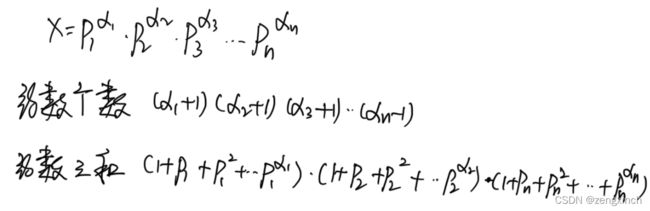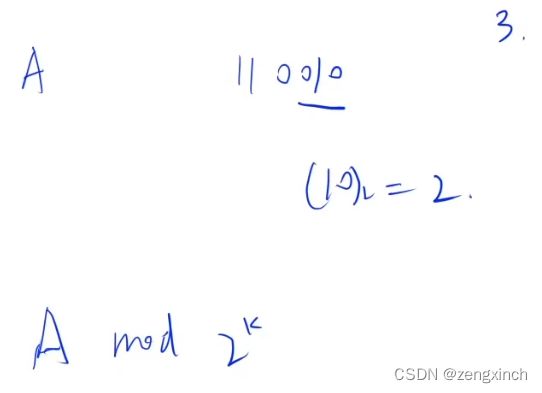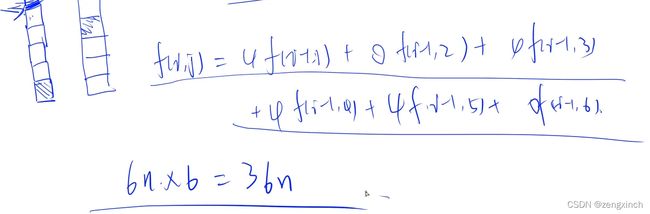AcWing 蓝桥杯C++ AB组辅导课学习记录(Python,备战蓝桥杯)Day31 - Day60
时间不够了,从20220221开始,周一到周五每天:2-4题,周末每天:4-8题。
Day 31 (2022.2.12)
![]()
# acwing 1224. 交换瓶子
if __name__ == '__main__':
n = int(input())
arr = [0]+[int(x) for x in input().split()]
st, cnt = [0]*(n+1), 0
for i in range(1,n+1):
if not st[i]:
cnt += 1
while not st[i]:
st[i] = 1
i = arr[i]
print(n-cnt)Day 32 (2022.2.13)
今天复习了下树状数组和线段树,然后油漆面积和三体攻击就没有认真研究了,感觉很有难度,可以先放一放。
# acwing 1228. 油漆面积
if __name__ == '__main__':
n = int(input())
arr, x_max, y_max = [], 0, 0
for _ in range(n):
square = [int(x) for x in input().split()]
x_max, y_max = max(x_max, square[2]), max(y_max, square[3])
arr.append(square)
squares = [[0]*y_max for _ in range(x_max)]
for i in range(n):
x1,y1,x2,y2 = arr[i]
for x in range(x1,x2):
for y in range(y1,y2):
squares[x][y] = 1
res = 0
for i in range(x_max):
for j in range(y_max):
if squares[i][j]!=0: res+=1
print(res)Day 33 (2022.2.14)
# acwing 1240. 完全二叉树的权值
if __name__ == '__main__':
n = int(input())
arr = [0] + [int(x) for x in input().split()]
depth, v_max, depth_max = 0, -float('inf'), 1
width, i = 1, 1
while i <= n:
tmp_v, depth = 0, depth+1
for j in range(width):
if i+j <= n: tmp_v += arr[i+j]
if tmp_v > v_max:
depth_max = depth
v_max = tmp_v
i += width
width *= 2
print(depth_max)完全二叉树的性质:1. 每一层节点编号从 2^(n-1) - 2^n-1
2. 每一层节点数 2^(n-1)
3. 树的深度 floor(log2(n))+1
Day 34 (2022.2.15)
# acwing 1096. 地牢大师
from collections import deque
directions = [(0,1,0),(0,-1,0),(0,0,1),(0,0,-1),(1,0,0),(-1,0,0)]
def bfs(x,y,z):
q = deque()
q.append([x,y,z])
while q:
l_cur, r_cur, c_cur = q.popleft()
for direction in directions:
l_tmp, r_tmp, c_tmp = l_cur + direction[0], r_cur + direction[1], c_cur + direction[2]
if l_tmp>=0 and l_tmp=0 and r_tmp=0 and c_tmp Day 35 (2022.2.16)
![]()
Day 36 (2022.2.17)
# acwing 154. 滑动窗口
N = 1000010
# 如果队列中存在两个元素,满足 a[i] >= a[j] 且 i < j,那么无论在什么时候我们都不会取
# a[i] 作为最小值了,所以可以直接将 a[i] 删掉;
# 此时队列中剩下的元素严格单调递增,所以队头就是整个队列中的最小值,可以用 O(1) 的时间找到;
# 为了维护队列的这个性质,我们在往队尾插入元素之前,先将队尾大于等于当前数的元素全部弹出即可;
# 这样所有数均只进队一次,出队一次,所以时间复杂度是 O(n) 的。
if __name__ == '__main__':
n, k = map(int, input().split())
hh, tt = 0, -1
arr, q = [int(x) for x in input().split()], [0]*N
for i in range(n):
if i-k+1 > q[hh]: hh+=1 # i-k+1是新的队头:解决队首已经出窗口的问题;
while hh<=tt and arr[i]<=arr[q[tt]]: tt-=1 # 解决队尾与当前元素a[i]不满足单调性的问题;
tt, q[tt] = tt+1, i # 将当前元素下标加入队尾;
if i+1 >= k: print(arr[q[hh]], end=' ') # 如果满足条件则输出结果;
hh, tt = 0, -1
print()
for i in range(n):
if i-k+1 > q[hh]: hh+=1
while hh<=tt and arr[i]>=arr[q[tt]]: tt-=1
tt, q[tt] = tt+1, i
if i+1 >= k: print(arr[q[hh]], end=' ')Day 37 (2022.2.18)
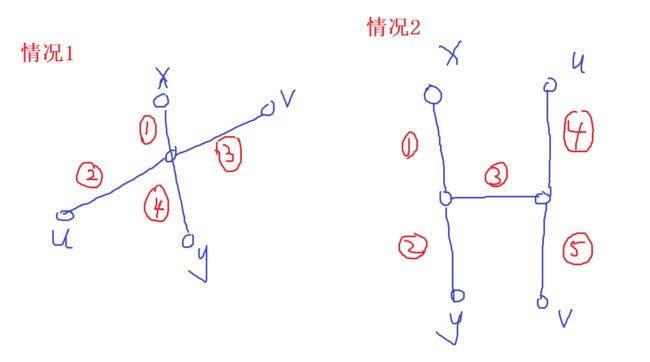
由于题目说到不重复经过大城市,从首都到达每个大城市的方案都是唯一的。因此可以知道该图是一棵树,本题求的是树的直径
树的直径:树中长度最长的路径
1、任取一点x
2、找到距离x最远的点y
3、从y开始遍历,找到离y最远的点,与y最远的点的距离是树的直径
证明:y一定是树的直径的端点
假设y不是树的直径的端点,分两种情况,如图所示,其中uv是树的直径
情况1:由于y是离x最远的点,因此 4>2, 4>3 推出2+4 > 2+3,与2+3为直径矛盾
情况2:2>(3+4), 2>(3+5) 推出2+3+4 > 4+5,与4+5为直径矛盾,因此y一定是树的直径的端点。
# acwing 1207. 大臣的旅费
import sys
sys.setrecursionlimit(5000)
def add(a,b,c):
global idx
e[idx], w[idx], ne[idx], h[a], idx = b, c, h[a], idx, idx+1
def dfs(u,father,distance):
dist[u] = distance
i = h[u]
while i!=-1:
j = e[i]
if j!=father: dfs(j,u,distance+w[i])
i = ne[i]
if __name__ == '__main__':
n = int(input())
N, M = n+10, n*2+10
h, e, ne, w, idx = [-1]*N, [0]*M, [0]*M, [0]*M, 0
dist = [0]*N
for _ in range(n-1):
a,b,c = map(int, input().split())
add(a,b,c)
add(b,a,c)
dfs(1,-1,0)
u = 1
for i in range(2,n+1):
if dist[i]>dist[u]: u=i
dfs(u,-1,0)
for i in range(1,n+1):
if dist[i]>dist[u]: u=i
print(dist[u]*10 + dist[u]*(dist[u]+1)//2)# acwing 1207. 大臣的旅费
from collections import deque
def add(a,b,c):
global idx
e[idx], w[idx], ne[idx], h[a], idx = b, c, h[a], idx, idx+1
def bfs(u):
q = deque([u])
st = [0] * (n+1)
st[u], dist[u] = 1, 0
while q:
x = q.popleft()
index = h[x]
while index != -1:
y = e[index]
if not st[y]:
st[y], dist[y] = 1, dist[x]+w[index]
q.append(y)
index = ne[index]
if __name__ == '__main__':
n = int(input())
N, M = n+10, n*2+10
h, e, ne, w, idx = [-1]*N, [0]*M, [0]*M, [0]*M, 0
dist = [0]*N
for _ in range(n-1):
a,b,c = map(int, input().split())
add(a,b,c)
add(b,a,c)
bfs(1)
u = 1
for i in range(2,n+1):
if dist[i]>dist[u]: u=i
bfs(u)
for i in range(1,n+1):
if dist[i]>dist[u]: u=i
print(dist[u]*10 + dist[u]*(dist[u]+1)//2)Day 38 (2022.2.19)
不同交易之间日期不能够重叠,每个交易都可拆分成隔日交易的累加
# acwing 1055. 股票买卖 II
if __name__ == '__main__':
n = int(input())
arr = [0] + [int(x) for x in input().split()]
for i in range(2,n+1):
arr[0] += max(0, arr[i]-arr[i-1])
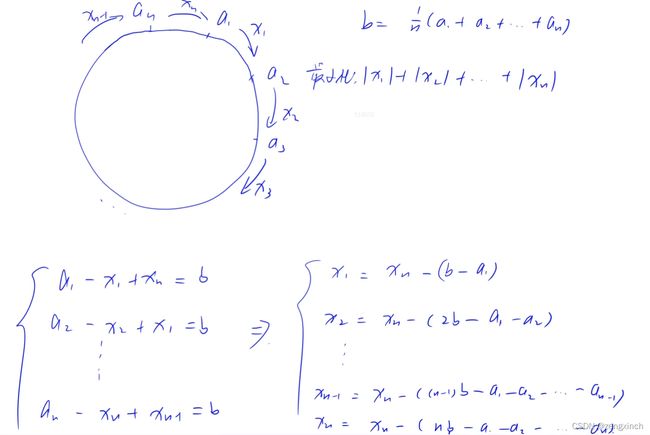
print(arr[0])1 用数学公式先把问题构造出来(最后一项nb-a1-a2...为0,因此xn=xn)
2 最后求解公式为红色部分,其等价与货舱问题
3 怎么证明这种给法一定有解呢,不存在a=5,却要给10的情况呢。
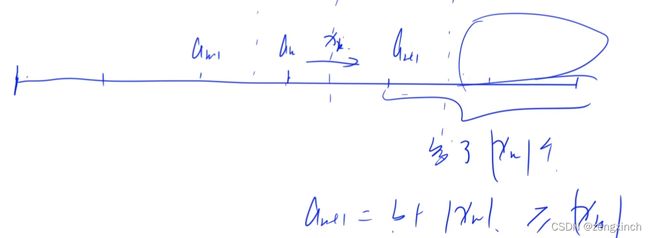
我们可以知道某些x是>=0,某些是<0,因为如果都大于0,那么每个x就可以同时减去一个数,而不改变最终结果。给的顺序是左边往右边给,如果是>0就马上给,如果是<0先等着>0的给完了再从右边给回来
4 假设ak给ak+1 xk个,首先可以知道a1+a...+ak-1<=(k-1),因为有可能从ak拿一些过来。而ak又要给ak+1 xk个,说明a1+a...+ak=bk+xk个 (这背后有个已经存在的条件,就是每个a肯定可以变成b或者说是尽最大努力的靠拢)
# acwing 122. 糖果传递
if __name__ == '__main__':
n = int(input())
arr, arr_pre, total = [0], [0], 0
for i in range(1,n+1):
arr.append(int(input()))
arr_pre.append(arr[i] + arr_pre[i-1])
b = sum(arr)//n
for i in range(1,n+1):
arr_pre[i] = i*b - arr_pre[i]
arr_pre.pop(0)
arr_pre.sort()
for i in range(n):
total += abs(arr_pre[i] - arr_pre[n//2])
print(total)Day 39 (2022.2.20)
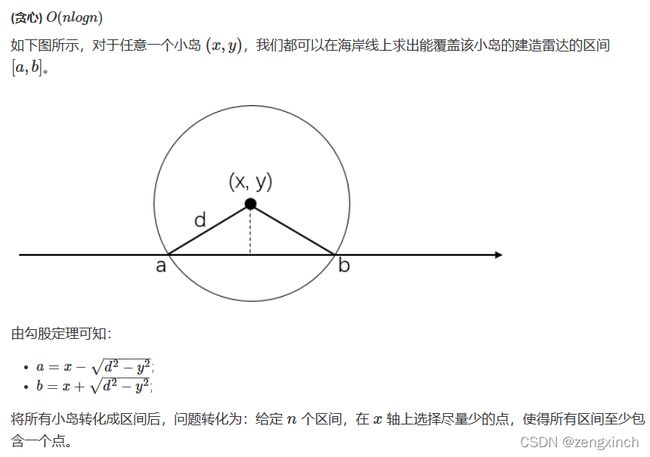
# acwing 112. 雷达设备
import math
if __name__ == '__main__':
n, d = map(int, input().split())
arr = []
for _ in range(n):
x, y = map(int, input().split())
if y>d:
print('-1')
exit()
arr.append([x - math.sqrt(d**2-y**2), x + math.sqrt(d**2-y**2)])
arr.sort(key=lambda x:x[1])
total, pt = 0, -float('inf')
for i in range(n):
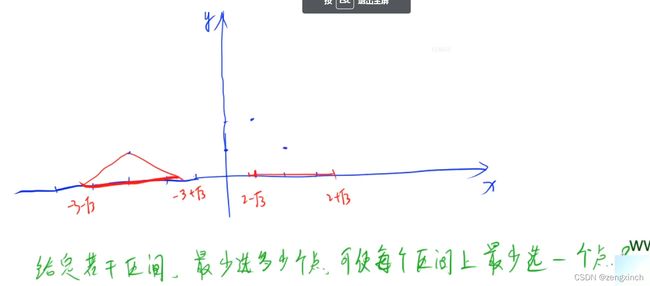
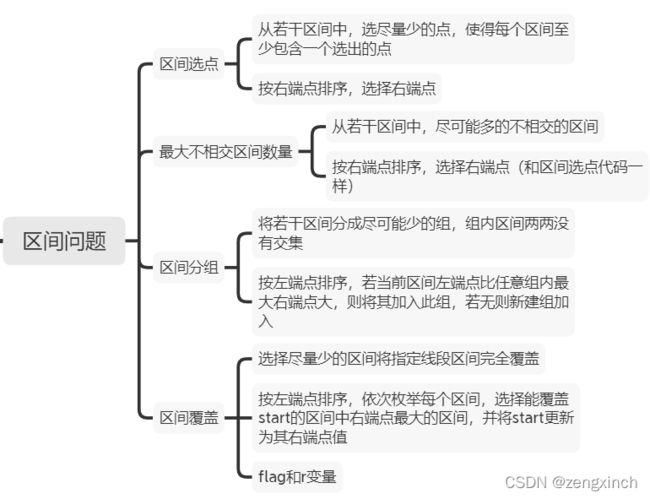
if pt今天总结了贪心的区间问题:
Day 40 (2022.2.21)
# acwing 1235. 付账问题
import math
if __name__ == '__main__':
n, s = map(int, input().split())
arr, ans = [int(x) for x in input().split()], [0]*n
arr.sort()
ave = s/n
pos = 0
for i in range(n):
if ave>arr[i]:
pos += ave-arr[i]
ans[i] = arr[i]
else:
if arr[i]-ave>pos/(n-i):
ans[i]=ave+pos/(n-i)
pos = pos - pos/(n-i)
else:
ans[i] = arr[i]
pos = pos - arr[i] + ave
total = 0
for i in range(n):
total += (ans[i]-ave)**2
print('{:.4f}'.format(math.sqrt(total/n)))# acwing 1235. 付账问题
# decimal 求高精度,但是速度很慢
from math import *
from decimal import *
getcontext().prec = 20
if __name__ == '__main__':
n, s = map(int, input().split())
arr, ans = [int(x) for x in input().split()], [0]*n
arr.sort()
ave = Decimal(s) / Decimal(n)
pos = Decimal(0)
for i in range(n):
if ave>arr[i]:
pos += ave-arr[i]
ans[i] = Decimal(arr[i])
else:
if arr[i]-ave>pos/(n-i):
ans[i]= ave+pos/(n-i)
pos = pos - pos/(n-i)
else:
ans[i] = arr[i]
pos = pos - arr[i] + ave
total = 0
for i in range(n):
total += (ans[i]-ave)**2
print('{:.4f}'.format(sqrt(total/n)))
还复习了 148 合并果子。
Day 41 (2022.2.22)
这个乘积最大真的是把我绕晕了。
# acwing 1239. 乘积最大
N = 1000000009
if __name__ == '__main__':
n, k = map(int, input().split())
arr, res = [], 1
for _ in range(n): arr.append(int(input()))
arr.sort()
l, r = 0, n-1
if k%2:
res = arr[r]
r, k = r-1, k-1
tmp_res = 1
while k:
x, y = arr[l]*arr[l+1], arr[r]*arr[r-1]
if (x>y and res<0) or (x=0):
tmp_res = y * tmp_res % N
r -= 2
else:
tmp_res = x * tmp_res % N
l += 2
k -= 2
if res<0: print(0-(0-res*tmp_res)%N)
else: print(res*tmp_res%N)
# acwing 1239. 乘积最大
# 能通过10个,else: negflag, posflag = 0, 0这个else分支没考虑完全
N = 1000000009
def negmod(x):
return 0-((0-x)%N)
if __name__ == '__main__':
n, k = map(int, input().split())
arr, st = [], [0]*n
for _ in range(n): arr.append(int(input()))
arr.sort(key=lambda x:abs(x))
res, neg = 1, 0
for i in range(n-1,-1,-1):
if n-k+1==i:
if i==1:
if arr[1]*arr[0]*res>=0: res = res*arr[1]*arr[0]%N
else: res = negmod(res*arr[1]*arr[0])
break
if not neg%2:
ans1,ans2,ans3 = arr[i]*arr[i-2], arr[i-1]*arr[i-2],arr[i]*arr[i-1]
m_max = max(ans1,ans2,ans3)
if m_max*res<0: res = negmod(res*m_max)
else: res = res*m_max%N
break
else:
negflag, posflag = 0, 0
while i>=0 and posflag and negflag:
if arr[i]>=0 and not posflag:
posflag = 1
if res*arr[i]<0: res = negmod(res*arr[i])
else: res = res*arr[i]%N
if arr[i] >= 0 and not negflag:
negflag = 1
if res * arr[i] < 0: res = negmod(res * arr[i])
else: res = res * arr[i] % N
i -= 1
break
if arr[i]<0: neg+=1
if arr[i]*res<0: res = negmod(res * arr[i])
else: res = res*arr[i]%N
print(res)
还复习了913排队打水。
Day 42 (2022.2.23)
# acwing 1247. 后缀表达式
# 后缀表达式又称逆波兰表达式,明显的特点是:
# 逆波兰表达式中没有括号,计算时将操作符之前的第一个数作为右操作数,
# 第二个数作为左操作数,进行计算,得到的值继续放入逆波兰表达式中
# 后序遍历:左右根
if __name__ == '__main__':
n, m = map(int, input().split())
arr, total = [int(x) for x in input().split()], 0
arr.sort()
if m==0: total = sum(arr)
else:
total = arr[-1]-arr[0]
for i in range(1,n+m): total += abs(arr[i])
print(total)复习了 125 推公式 耍杂技的牛。
Day 43 (2022.2.24)
第一步:1.使用一次灵能传输相当于两个前缀和交换位置 2.求ai的相当于求si-s(i-1) 3.加一个s0=0,因为第一个数是和0作减法
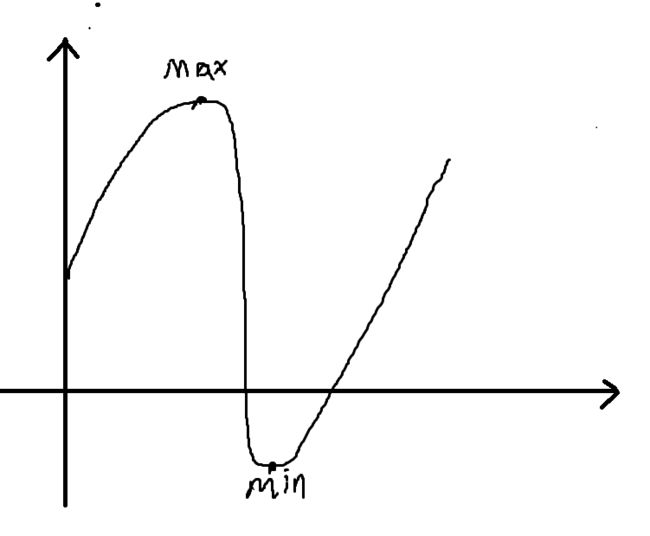
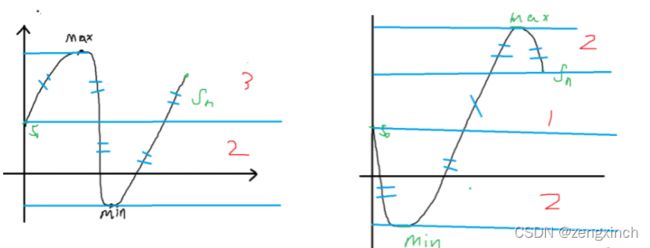
第二步:同一前缀和序列怎样排序使得max(|s[i] - s[i-1]|)最小,利用贪心的思路知:有序的前缀和序列使得所求最小
一个序列一定存在一个最大值和一个最小值,如果不是有序序列的话,即最大值和最小值不在两边的时候,最大值和最小值中间的点就少了,差值就变大了
第三步:s0 和 sn 不能计算到排序中,因为a0 和 an 在两边导致s0 和 sn的 位置固定,我们无法修改这两个数的位置,那么就使得我们最终得到的si序列不是单调的。这里假设s0 是小于sn的(如果是大于,swap一下,两种情况是对称的)
在s[0]到达s数组的最小值的过程中,如果一步到达,那么差值一定会很大,但是如果分几步到达会更好。到s[n]同理。
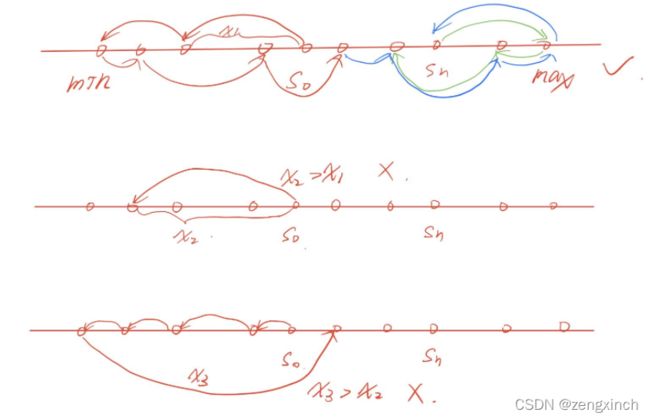
第一个图的在y轴视角的叠次数更多,而第二个图的重叠次数更少,重叠次数少则一段线上分布的点多,则差值小
第四步:为什么跳着选点,是因为2->3,那么从4->1肯定大于2->4,4->3,3->1
# acwomg 1248. 灵能传输
N = 300010
if __name__ == '__main__':
t = int(input())
for _ in range(t):
n = int(input())
arr, st, s = [0] + [int(x) for x in input().split()], [0]*(n+1), [0]*(n+1)
for i in range(1,n+1): s[i] = s[i-1] + arr[i]
s0, sn = min(s[0], s[n]), max(s[0], s[n])
s.sort()
for i in range(n+1):
if s[i]==s0:
s0=i
break
for i in range(n,-1,-1):
if s[i]==sn:
sn=i
break
l, r = 0, n
for i in range(s0,-1,-2):
arr[l], st[i], l = s[i], 1, l+1
for i in range(sn,n+1,2):
arr[r], st[i], r = s[i], 1, r-1
for i in range(n+1):
if not st[i]: arr[l], l = s[i], l+1
res = 0
for i in range(1,n+1): res = max(res, abs(arr[i]-arr[i-1]))
print(res)
还复习了01背包问题。
Day 44 (2022.2.25)
复习了完全背包问题和多重背包问题简单版。
Day 45 (2022.2.26)
# acwing 1246. 等差数列
def gcd(a,b):
return gcd(b,a%b) if b else a
if __name__ == '__main__':
n = int(input())
arr, d = [int(x) for x in input().split()], 0
arr.sort()
for i in range(1,n): d = gcd(d,arr[i]-arr[i-1])
if not d: print(n)
else: print((arr[-1]-arr[0])//d+1)今天还复习了多重背包问题II、分组背包问题和最大公约数。
Day 46 (2022.2.27)
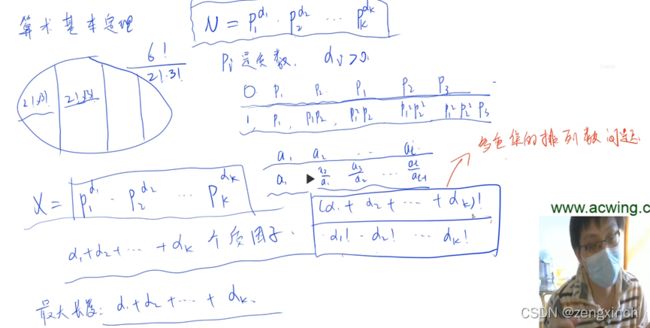
公理是大家都认可的但没法证明的认知,定理是可以由其它公理或定理推论出来的结论
多重全排列:
from math import *
from sys import *
def get_primes():
global x
for i in range(2, int(sqrt(x)) + 1):
if x % i == 0:
s = 0
while x % i == 0:
s += 1
x //= i
primes.append(s)
if x > 1: primes.append(1)
if __name__ == '__main__':
while True:
x = stdin.readline().strip('\n')
if not x: break
x, primes = int(x), []
get_primes()
length = sum(primes)
num = factorial(length)
for i in range(len(primes)):
num //= factorial(primes[i])
print(length, num)
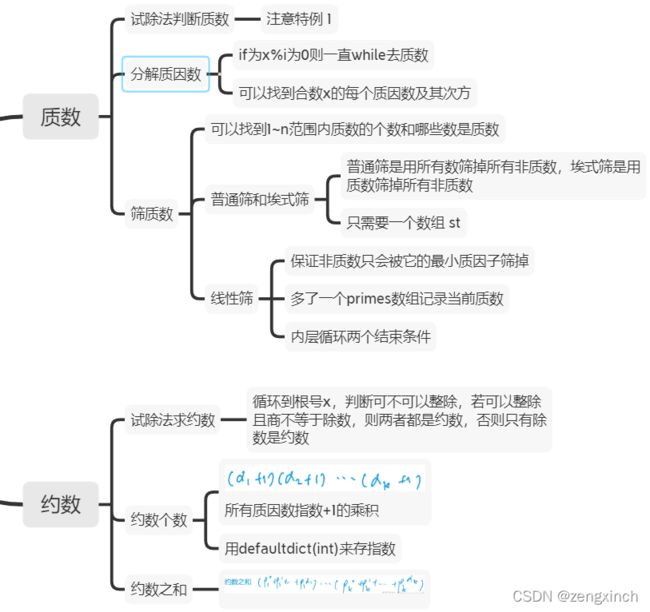
复习了质数和约数的题(共7题)
Day 47 (2022.2.28)
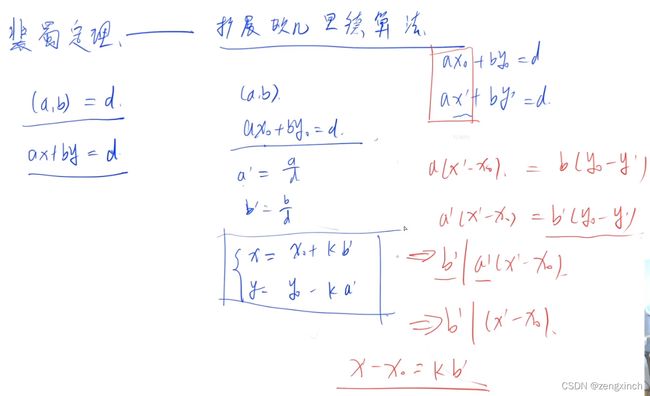
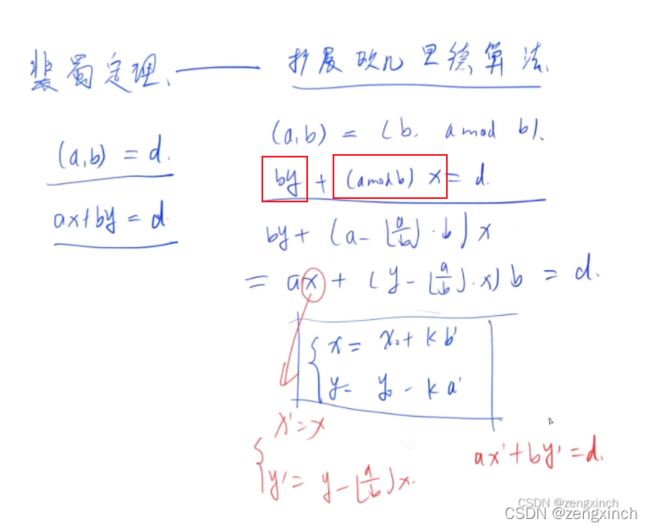
对于这道题来说,若x>=s,则x必然有两个因子,一个1一个x,那么其约数一定大于s,因此1 假设x的约数是(1+2)(1+3+3^2)...(1+p+p^2...+p^n) 只需要几个数(一个括号算一个)的量级就非常大了。这个时候就可以想到用dfs来做。 当枚举到 ai=1 xxx这句话不看,好像没啥用(AcWing 1296. 聪明的燕姿 - AcWing) last 表示上一个枚举的质数是谁 prod 表示当前计算到的s的每个括号中最高次项的和,若枚举到p2^a2,则其等于p1^a1*p2^a2。 s 表示 s/(1+p1^1+p1^2+...+p1^a1)...(1+pk^1+pk^2+...+pk^ai)的乘积 Day 48 (2022.3.1) 这里y应该是新的x,x应该是新的y Day 49 (2022.3.2) Day 50 (2022.3.3) k位系统就是每次都要模商2的k次方(默认都是无符号整数),如3位系统的110010就只会保留 010=2。 还复习了878线性同余方程,1299 1323 1301都是线性同余方程的扩展 Day 51 (2022.3.4) 今天还复习了873欧拉函数。 Day 52 (2022.3.5) 这是一个重复覆盖问题,重复覆盖又是一个很经典的问题,优化方式有三种。(解释看代码) (这道题不用可行性剪枝 h() 可以ac,用了反而不能ac,感觉是行数大的时候用剪枝) 思路是上述的思路,对代码的优化有状态压缩和lowbit来找到违背覆盖的列。 今天还复习了 831 kmp、842 排列数字和 843 n-皇后问题。 Day 53 (2022.3.6) 这道题首先需要转变思路,原题求从回文串脱落了多少种子变成了现在这样子。那我们可以反过来,求现在这个串里面的最大回文串长度是多少,剩下的不匹配字符(不能够被添加到现在最大回文串的字符,就对应着原来脱落掉的字符) 例:ABDCDCBABC ,他现在最大回文串为ABDCDBA,其中C BC没有被匹配在里面,说明其对应的字符脱落掉了。 因此,最终的答案可以转换为 当前串长度-当前串中最长回文串的长度。 求当前串最长回文串的长度就不得不先去看下 897. 最长公共子序列,其状态表示和状态计算都十分相似。 思路:左右端点选或不选,左端点选则=f[l.r-1],右端点一样,都不选的情况包含在了前面两种情况中,都选则为f[l+1,r-1]+2,当必须满足要求s[l]==s[r]。 AcWing 1222. 区间$DP$(大白话详解) - AcWing AcWing 1222. 密码脱落 - AcWing Day 54 (2022.3.7) 还复习了 285 没有上司的舞会 Day 55 (2022.3.8) 898 数字三角形 直接对全局变量进行重新赋值是需要声明global的,但修改其中的部分值不用。f = [1,2,3],令f= xxx要声明, f[1]=1不用。 Day 56 (2022.3.9) 今天复习了快速幂和快速幂、扩展欧几里得算法求逆元 Day 57 (2022.3.10) AcWing 1226. 包子凑数 完全背包 ($yan氏dp + 层层分析$) - AcWing Day 58 (2022.3.11) Day 59 (2022.3.12) Day 60 (2022.3.13) 矩阵快速幂 假设只有两个骰子,f(M)是下面那个骰子,矩阵A是上面那个骰子。当上面的骰子顶端是1的时候,它可以旋转四次,这个时候下面骰子可以换6个点,每个点旋转四次。 当f(M)和第一列相乘,①乘①表示下面的骰子1在顶端,然后上下两个骰子都可以旋转4次(4x4),②乘②表示下面的骰子2在顶端,两个骰子都可以旋转4次。。。第一列就代表上面的骰子顶端是1。因此,假设1和2不能相邻,则下面骰子顶端是1上面骰子顶端是5的时候不行,即A的第一行第五列为0. ----------------------------# acwing 1296. 聪明的燕姿
from sys import *
from math import *
N = 50000
def get_primes(n):
global cnt
for i in range(2,n+1):
if not st[i]:
primes[cnt], cnt = i, cnt+1
for j in range(cnt):
if primes[j]>n/i: break
st[i*primes[j]] = 1
if i%primes[j]==0: break
def is_prime(x):
if x![]()
# acwing 1299. 五指山
def exgcd(a, b):
if not b: return 1, 0, a
x1, y1, d1 = exgcd(b, a%b)
return y1, x1-(a//b)*y1, d1
if __name__ == '__main__':
t = int(input())
for _ in range(t):
n, d, x, y = map(int, input().split())
x0, y0, d0 = exgcd(n, d)
if (y-x)%d0: print('Impossible')
else:
y0 *= (y-x)//d0
n //= d0
print(y0%n)
# else后面的解释如下图:# acwing 1223. 最大比例
# 这个算法纯粹自己写的
from math import *
from collections import *
def get_primes(x):
tmp_arr = defaultdict(int)
for i in range(2,int(sqrt(x))+1):
if x%i==0:
s = 0
while x%i==0:
s+=1
x//=i
tmp_arr[i] += s
keys.add(i)
if x>1:
tmp_arr[x] += 1
keys.add(x)
return tmp_arr
def gcd(a,b):
return a if not b else gcd(b,a%b)
if __name__ == '__main__':
n = int(input())
keys = set()
arr = [int(x) for x in input().split()]
arr_set = list(set(arr))
arr_set.sort()
arr_min = get_primes(arr_set[0])
arr_max = get_primes(arr_set[-1])
for key in keys:
arr_max[key] -= arr_min[key]
d = 0
for key in keys:
d = gcd(d,abs(arr_max[key]))
length = len(arr_set)-1
lengths = []
while d>=length:
if d%length==0:
lengths.append(length)
length += 1
fenzi, fenmu, ans = 1, 1, []
for i in range(len(lengths)):
for key in keys:
tmp = arr_max[key]//lengths[i]
if tmp>0: fenzi = fenzi*key**tmp
else: fenmu = fenmu*key**abs(tmp)
ans.append([fenzi,fenmu])
fenzi, fenmu = 1, 1
fenzi, fenmu = ans[-1][0], ans[-1][1]
for i in range(len(ans)-1):
if ans[i][0]/ans[i][1] > fenzi/fenmu:
fenzi, fenmu = ans[i][0], ans[i][1]
print("{:d}/{:d}".format(fenzi, fenmu))# acwing 1301. C循环
def exgcd(a,b):
if not b: return 1, 0, a
x1, y1, d1 = exgcd(b,a%b)
return y1, x1-(a//b)*y1, d1
if __name__ == '__main__':
while True:
A,B,C,k = map(int, input().split())
if A==B==C==k==0: break
k = 2**k
x0, y0, d0 = exgcd(C,k)
if (B-A)%d0: print("FOREVER")
else:
x0 *= (B-A)//d0
k //= d0
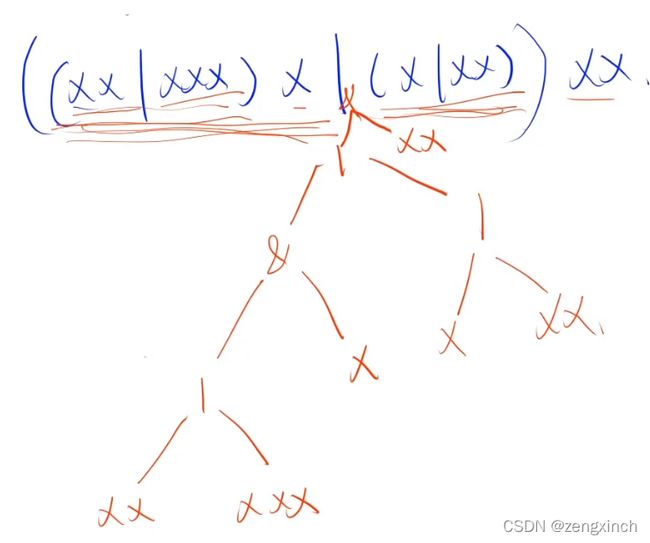
print(x0%k)# acwing 1225. 正则问题
# 递归都会定义一棵树
# 这道题估计也可以分情况讨论,只是要注意情况的完整度
# 先把思路整理好再写代码
# 四则运算因为符号多(+-*/)所以不用递归做
def dfs():
global k
res = 0
while k![]()
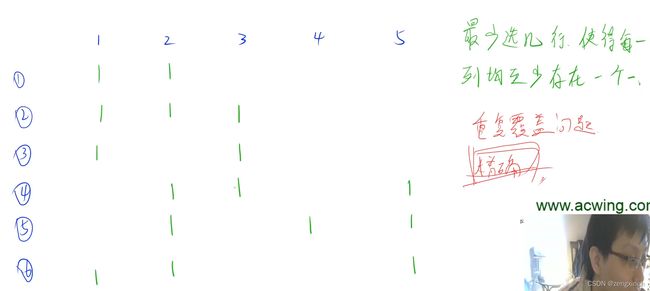
# 最好的做法是dancing links
# 这里用一个比较快的,也比较好写的一个算法
# 最原始思路:每次找到一个未被覆盖的列,依次枚举所有包含它的行
# 每次枚举选一行,然后递归到下一列
# 优化:迭代加深,每次枚举一行够不够,枚举两行够不够。。。
# 每次找选择最少的列
# 可行性剪枝 (最少要选多少行才可以覆盖所有列)
# 位运算来进行优化 lowbit
N, M = 110, 1<<20
def lowbit(x):
return x&-x
def h(state):
# i表示达到所有列都有糖果的状态还差哪些列,1表示差,0表示有
res, i = 0, (1<# acwing 1050. 鸣人的影分身
def dfs(u, l, r):
path.sort()
if u == n - 1:
if r >= m - sum(path):
path.append(m - sum(path))
arr.add("".join(map(str, sorted(path[:]))))
path.pop()
return
for i in range(l, r + 1):
path.append(i)
dfs(u + 1, i, r - i)
path.pop()
if __name__ == '__main__':
t = int(input())
for _ in range(t):
m, n = map(int, input().split())
arr, path = set(), []
dfs(0, 0, m)
print(len(arr))# acwing 1050. 鸣人的影分身
# DP问题除了想到状态表示和状态计算(注意集合划分的某些子集是否存在进入条件),还得确认初始条件
if __name__ == '__main__':
t = int(input())
for _ in range(t):
m, n = map(int, input().split())
f = [[0]*(n+1) for _ in range(m+1)]
for i in range(n+1): f[0][i] = 1
for i in range(1,m+1):
for j in range(1,n+1):
f[i][j] = f[i][j-1]
if i>=j: f[i][j] += f[i-j][j]
print(f[m][n])
![]()
# acwing 1047. 糖果
# 背包:选择模型,从一堆物品选出一个子集,满足一个条件
# 背包问题一般i是数量,j是限制条件相关
# p(0,0)=0,dp(0,i)(i≠0)dp(0,0)=0,dp(0,i)(i≠0)都是不合法的状态,所以必须要初始化为负无穷
# 初始化为负无穷后,后续在不合法状态上衍生的结果都远远小于0
if __name__ == '__main__':
n, k = map(int, input().split())
candies, f = [0], [[-float('inf')]*k for _ in range(n+1)]
f[0][0] = 0
for _ in range(n):
candies.append(int(input()))
for i in range(1,n+1):
for j in range(k):
f[i][j] = max(f[i-1][j], f[i-1][(j-candies[i])%k] + candies[i])
print(f[n][0])# acwing 1222. 密码脱落
if __name__ == '__main__':
password = input()
n = len(password)
f = [[0]*(n+1) for _ in range(n+1)]
for length in range(1,n+1):
for l in range(n):
r = l+length-1
if r>=n: break
if length==1: f[l][r] = 1
else:
f[l][r] = max(f[l+1][r], f[l][r-1])
if password[l]==password[r]: f[l][r] = max(f[l][r], f[l+1][r-1]+2)
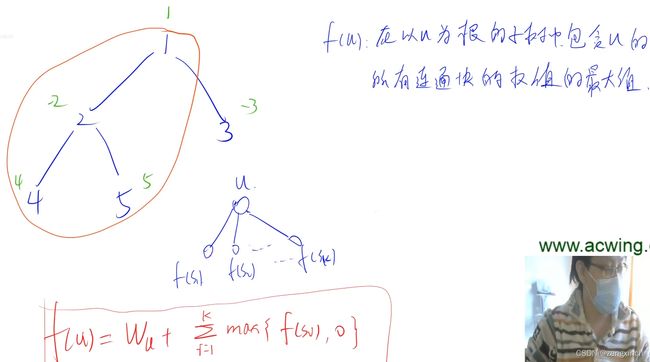
print(n - f[0][n-1])# acwing 1220. 生命之树
# 树形dp,一般用递归或者dfs,每次以子树为单位来计算(子树的根节点)
# 需要计算的次数是边的数量
def add(a,b):
global idx
e[idx], ne[idx], h[a], idx = b, h[a], idx, idx+1
def dfs(u, father):
f[u] = w[u]
idx_d = h[u]
while idx_d!=-1:
b_d = e[idx_d]
if b_d!=father:
dfs(b_d, u)
f[u] += max(0, f[b_d])
idx_d = ne[idx_d]
if __name__ == '__main__':
n = int(input())
w, e, ne, h, f, idx = [0] + [int(x) for x in input().split()], [0]*2*(n+10), [0]*2*(n+10), [-1]*(n+10), [0]*(n+10), 0
for _ in range(n-1):
a, b = map(int, input().split())
add(a,b)
add(b,a)
dfs(1,-1)
print(max(f[1:n+1]))![]()
# acwing 1303. 斐波那契前n项和
# 矩阵快速幂
def mulf():
out = [0,0,0]
out[0] = (f1[0]*a[0][0] + f1[1]*a[1][0] + f1[2]*a[2][0])%m
out[1] = (f1[0]*a[0][1] + f1[1]*a[1][1] + f1[2]*a[2][1])%m
out[2] = (f1[0]*a[0][2] + f1[1]*a[1][2] + f1[2]*a[2][2])%m
return out
def mula():
out = [[0]*3 for _ in range(3)]
for i in range(3):
for j in range(3):
out[i][j] = (a[i][0]*a[0][j] + a[i][1]*a[1][j] + a[i][2]*a[2][j])%m
return out
if __name__ == '__main__':
n, m = map(int, input().split())
f1, a = [1,1,1], [[0,1,0],[1,1,1],[0,0,1]]
n -= 1
while n:
if n&1: f1 = mulf() # f = f*a
a = mula() # a = a*a
n >>= 1
print(f1[2])from math import *
N = 10000
if __name__ == '__main__':
n = int(input())
arr, d = [0], 0
for _ in range(n):
arr.append(int(input()))
d = gcd(d,arr[-1])
if d!=1: print('INF')
else:
f = [[0]*N for _ in range(n+1)]
f[0][0] = 1
for i in range(1,n+1):
for j in range(N):
f[i][j] |= f[i-1][j]
if j>=arr[i]: f[i][j] |= f[i][j-arr[i]]
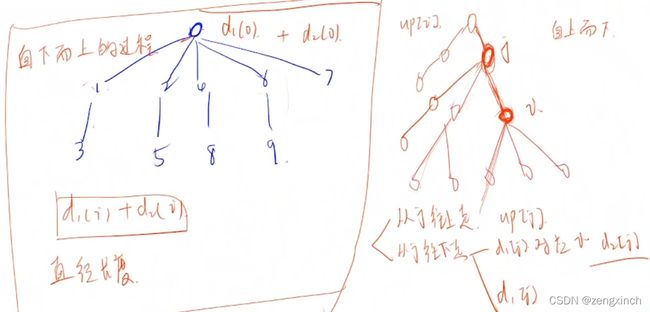
print(N-sum(f[n]))# 判断从这个点出发的所有值的最大值和次大值,
# dfs_d的话只能求出往下走的路径长度有几种
# 而这里还需要求出往上走的情况
# 它儿子的up值,就等于它的up值+1
# 如果它儿子是d1这条路径,则判断max(up+1,d2)
# 否则判断max(up+1,d1)
# acwing 1078. 旅游规划
def add(a,b):
global idx
e[idx], ne[idx], h[a], idx = b, h[a], idx, idx+1
# 利用儿子的节点更新当前节点
def dfs_d(u,father):
global maxd
idx = h[u]
while idx!=-1:
b = e[idx]
if b!=father:
dfs_d(b,u)
distance = d1[b]+1
if distance>d1[u]:
d2[u], d1[u], p1[u] = d1[u], distance, b
elif distance>d2[u]: d2[u] = distance
idx = ne[idx]
maxd = max(maxd, d1[u]+d2[u])
# 利用当前节点更新其儿子的节点
def dfs_u(u,father):
idx = h[u]
while idx!=-1:
b = e[idx]
if b!=father:
up[b] = up[u]+1
if p1[u]==b: up[b] = max(up[b],d2[u]+1)
else: up[b] = max(up[b],d1[u]+1)
dfs_u(b,u)
idx = ne[idx]
if __name__ == '__main__':
n = int(input())
h, e, ne, idx = [-1]*(n+10), [0]*2*(n+10), [0]*2*(n+10), 0
d1, d2, p1, up, maxd = [0]*(n+10), [0]*(n+10), [0]*(n+10), [0]*(n+10), 0
for _ in range(n-1):
a,b = map(int, input().split())
add(a,b)
add(b,a)
dfs_d(0, -1)
dfs_u(0, -1)
for i in range(n):
curList = sorted([d1[i], d2[i], up[i]])
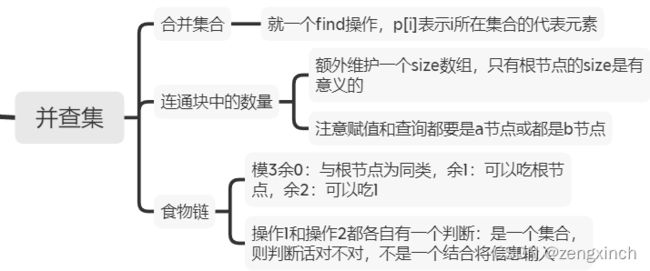
if sum(curList[1:3]) == maxd: print(i)# acwing 1242. 修改数组
import sys
sys.setrecursionlimit(99999)
N = 1100010
def find(x):
if x!=p[x]:
p[x] = find(p[x])
return p[x]
if __name__ == '__main__':
n = int(input())
p = [x for x in range(N)]
arr = [0]+[int(x) for x in input().split()]
for i in range(1,n+1):
x = find(arr[i])
print(x, end=' ')
p[x] = x+1![]()
![]()
# acwing 1070. 括号匹配
def is_match(a,b):
if (a=='(' and b==')') or (a=='[' and b==']'): return True
return False
if __name__ == '__main__':
s = ' ' + input()
n = len(s)-1
f = [[float('inf')]*(n+1) for _ in range(n+1)]
for dur in range(1,n+1):
for l in range(1,n-dur+2):
r = l+dur-1
if dur == 1: f[l][r] = 1
else:
if dur == 2:
if is_match(s[l],s[r]): f[l][r] = 0
else: f[l][r] = 2
else:
f[l][r] = min(f[l+1][r], f[l][r-1]) + 1
if is_match(s[l],s[r]): f[l][r] = min(f[l][r], f[l+1][r-1])
for k in range(l,r):
f[l][r] = min(f[l][r], f[l][k]+f[k+1][r])
print(f[1][n])# acwing 1217. 垒骰子
M = 1000000007
def opposite(x):
if x>=4: return x-3
else: return x+3
if __name__ == '__main__':
n, m = map(int, input().split())
st, f = set(), [[0]*7 for _ in range(n+1)]
for _ in range(m):
x, y = map(int, input().split())
st.add((x,y))
st.add((y,x))
f[1] = [0,4,4,4,4,4,4]
for i in range(2,n+1):
for j in range(1,7):
for k in range(1,7):
if (k,opposite(j)) in st: continue
f[i][j] = (f[i][j] + f[i-1][k]*4) % M
print(sum(f[n]) % M)![]()
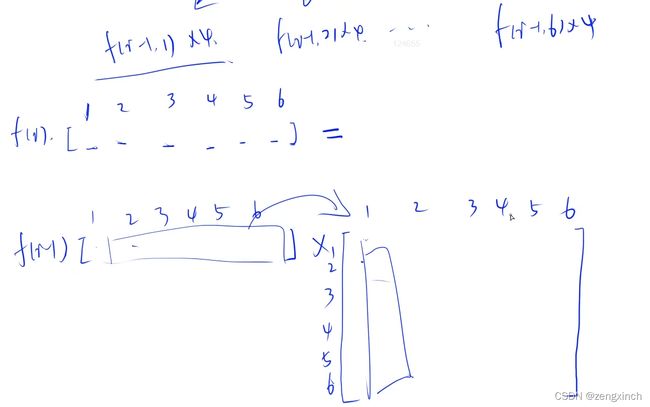
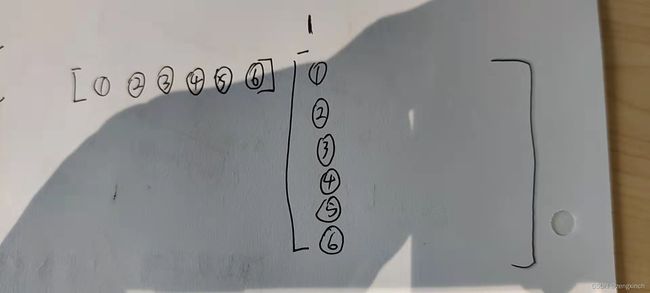
状态的数量是6n,转移的数量是6 (线性DP)
抽象成一个矩阵相乘的形式
把fi抽象成一个向量,由f(i-1)乘以一个矩阵转移过来
# acwing 1217. 垒骰子
M = 1000000007
def opposite(x):
if x>=3: return x-3
return x+3
def mul_res():
tmp_res = [0]*6
for i in range(6):
tmp_res[i] = (res[0]*A[0][i] + res[1]*A[1][i] + \
res[2]*A[2][i] + res[3]*A[3][i] + \
res[4]*A[4][i] + res[5]*A[5][i]) % M
return tmp_res
def mul_A():
tmp_A = [[0]*6 for _ in range(6)]
for i in range(6):
for j in range(6):
tmp_A[i][j] = (A[i][0]*A[0][j] + A[i][1]*A[1][j] + \
A[i][2]*A[2][j] + A[i][3]*A[3][j] + \
A[i][4]*A[4][j] + A[i][5]*A[5][j]) % M
return tmp_A
if __name__ == '__main__':
n, m = map(int, input().split())
res, A = [4,4,4,4,4,4], [[4]*6 for _ in range(6)]
for _ in range(m):
x, y = map(int, input().split())
A[x-1][opposite(y)-1], A[y-1][opposite(x)-1] = 0, 0
k = n-1
while k:
if k&1: res = mul_res()
A = mul_A()
k >>= 1
print(sum(res)%M)
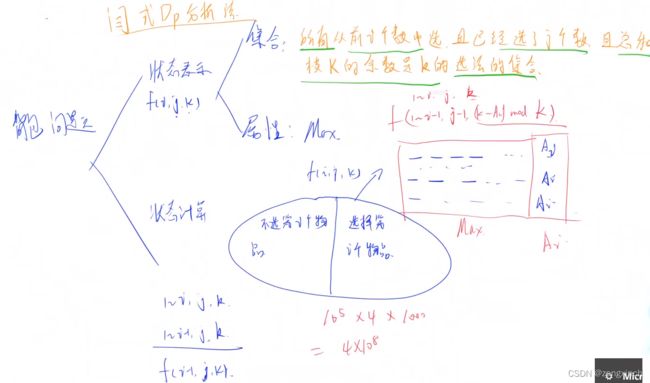
# acwing 1234. 倍数问题
# 这道题和 1047糖果 有很大联系
# 背包问题: 组合问题求最优解 (把限制加到状态表示里面)
# 余数相同的话尽量取较大的数(因此只需保留前三大的数,前三可能是考虑全选这三个的情况?)
N = 1001
if __name__ == '__main__':
n, m = map(int, input().split())
remainder, f = [[] for _ in range(N)], [[-float('inf')]*N for _ in range(4)]
arr = sorted([int(x) for x in input().split()], reverse=True)
for i in range(n):
remainder[arr[i]%m].append(arr[i])
f[0][0] = 0
# 前两个循环就是用贪心的思想把O(n)优化到了O(3m)
for i in range(m):
for u in range(min(3,len(remainder[i]))):
for j in range(3,0,-1):
for k in range(m):
f[j][k] = max(f[j][k], f[j-1][(k-remainder[i][u])%m] + remainder[i][u])
print(f[3][0])
#----------------------------------------------------------------------------------------
# DP暴力
# acwing 1234. 倍数问题
if __name__ == '__main__':
n, k = map(int, input().split())
arr = [0]+[int(x) for x in input().split()]
f = [[[-float('inf')]*(k) for _ in range(4)] for _ in range(n+1)]
for i in range(n+1): f[i][0][0] = 0
for i in range(1,n+1):
for j in range(1,4):
for kk in range(k):
f[i][j][kk] = max(f[i-1][j][kk], f[i-1][j-1][(kk-arr[i])%k]+arr[i])
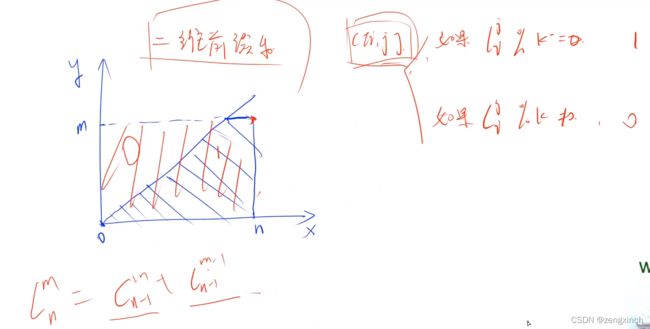
print(f[n][3][0])# acwing 523. 组合数问题
# 这道题告诉我前缀和必须要是一个矩阵全算
# c[i][j] = (c[i-1][j] + c[i-1][j-1])%k,模k和不模k的运算速度差距特大
N = 2010
if __name__ == '__main__':
t, k = map(int, input().split())
c, s = [[0]*N for _ in range(N)], [[0]*N for _ in range(N)]
for i in range(N):
c[i][0] = 1
for i in range(1,N):
for j in range(1,N):
if j<=i:
c[i][j] = (c[i-1][j] + c[i-1][j-1])%k
if c[i][j]==0: s[i][j] = 1
s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1]
for _ in range(t):
n, m = map(int, input().split())
print(s[n][m])
#----------------------------------------------------------------------------------------
# acwing 523. 组合数问题
N = 2010
if __name__ == '__main__':
t, k = map(int, input().split())
c, s = [[0]*N for _ in range(N)], [[0]*N for _ in range(N)]
for i in range(N):
for j in range(i+1):
if not j: c[i][j] = 1
else: c[i][j] = (c[i-1][j] + c[i-1][j-1]) % k
for i in range(N):
for j in range(N):
if j<=i and c[i][j]==0: s[i][j]=1
if i-1>=0: s[i][j] += s[i-1][j]
if j-1>=0: s[i][j] += s[i][j-1]
if i-1>=0 and j-1>=0: s[i][j] -= s[i-1][j-1]
for _ in range(t):
n, m = map(int, input().split())
print(s[n][m])