2022CCPC浙江省赛题解ABCGILM
2022CCPC浙江省赛题解ABCGILM
题目链接:
https://codeforces.com/gym/103687
讲义、代码链接:
https://hytidel.lanzoub.com/b031czgmf
密码:29i5
C. JB Wants to Earn Big Money
题意
输入 n ( 1 ≤ n ≤ 1 e 5 ) n\ \ (1\leq n\leq 1\mathrm{e}5) n (1≤n≤1e5)个范围为 [ 1 , 1 e 5 ] [1,1\mathrm{e}5] [1,1e5]的整数 a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an和 m ( 1 ≤ m ≤ 1 e 5 ) m\ \ (1\leq m\leq 1\mathrm{e}5) m (1≤m≤1e5)个范围为 [ 1 , 1 e 5 ] [1,1\mathrm{e}5] [1,1e5]的整数 b 1 , ⋯ , b m b_1,\cdots,b_m b1,⋯,bm.给定整数 x ( 1 ≤ x ≤ 1 e 5 ) x\ \ (1\leq x\leq 1\mathrm{e}5) x (1≤x≤1e5),统计 a [ ] a[] a[]中 ≥ x \geq x ≥x的数的个数和 b [ ] b[] b[]中 ≤ x \leq x ≤x的数的个数.
代码 -> 2022CCPC浙江省赛-C(模拟)
void solve() {
int n, m, x; cin >> n >> m >> x;
int ans = 0;
for (int i = 0; i < n; i++) {
int a; cin >> a;
if (a >= x) ans++;
}
for (int i = 0; i < m; i++) {
int b; cin >> b;
if (b <= x) ans++;
}
cout << ans;
}
int main() {
solve();
}
B. JB Loves Comma
题意
输入一个长度不超过 1 e 5 1\mathrm{e}5 1e5且只包含小写英文字母的字符串,在每个"cjb"后加逗号并输出.
代码 -> 2022CCPC浙江省赛-B(模拟)
void solve() {
char ch;
string ans;
while (cin >> ch) {
ans.push_back(ch);
if (ans.length() < 3) continue;
if (ans.substr(ans.length() - 3) == "cjb") ans.push_back(',');
}
cout << ans;
}
int main() {
solve();
}
A. JB Loves Math
题意
有 t ( 1 ≤ t ≤ 1 e 5 ) t\ \ (1\leq t\leq 1\mathrm{e}5) t (1≤t≤1e5)组测试数据.每组测试数据玩家选定一个正奇数 x x x和正偶数 y y y.给定两个整数 a , b ( 1 ≤ a , b ≤ 1 e 9 ) a,b\ \ (1\leq a,b\leq 1\mathrm{e}9) a,b (1≤a,b≤1e9),每次操作可令 a + = x a+=x a+=x或令 a − = y a-=y a−=y,途中不能修改 x x x和 y y y的值.求将 a a a变为 b b b的最小操作次数.
思路
(1)若 a = b a=b a=b,则无需操作.
(2)若 a < b aa<b:
①若 a a a与 b b b不同奇偶,则 a a a加 1 1 1次奇数 x = b − a x=b-a x=b−a即可.
②若 a a a与 b b b同奇偶,设 d i f f = b − a diff=b-a diff=b−a:
(i)若 ⌊ d i f f 2 ⌋ \left\lfloor\dfrac{diff}{2}\right\rfloor ⌊2diff⌋是奇数,如 a = 2 , b = 4 a=2,b=4 a=2,b=4时, a a a加 2 2 2次奇数 x = ⌊ d i f f 2 ⌋ x=\left\lfloor\dfrac{diff}{2}\right\rfloor x=⌊2diff⌋即可.
(ii)若 ⌊ d i f f 2 ⌋ \left\lfloor\dfrac{diff}{2}\right\rfloor ⌊2diff⌋是偶数,如 a = 2 , b = 6 a=2,b=6 a=2,b=6时, a a a先加 2 2 2次奇数 x = ⌊ d i f f 2 ⌋ + 1 x=\left\lfloor\dfrac{diff}{2}\right\rfloor+1 x=⌊2diff⌋+1,再减 1 1 1次偶数 y = 2 y=2 y=2即可.
(3)若 a > b a>b a>b:
①若 a a a与 b b b同奇偶,则 a a a减 1 1 1次偶数 y = a − b y=a-b y=a−b即可.
②若 a a a与 b b b不同奇偶,则 a a a减一次偶数 y = a − b + 1 y=a-b+1 y=a−b+1,再加一次奇数 x = 1 x=1 x=1即可.
代码 -> 2022CCPC浙江省赛-A(思维)
void solve() {
int a, b; cin >> a >> b;
if (a == b) {
cout << 0 << endl;
return;
}
else if (a < b) {
int diff = b - a;
if (diff & 1) cout << 1 << endl;
else {
if (diff / 2 & 1) cout << 2 << endl;
else cout << 3 << endl;
}
}
else {
if (abs(a - b) & 1) cout << 2 << endl;
else cout << 1 << endl;
}
}
int main() {
CaseT // 单测时注释掉该行
solve();
}
L. Candy Machine
题意
给定 n ( 1 ≤ n ≤ 1 e 6 ) n\ \ (1\leq n\leq 1\mathrm{e}6) n (1≤n≤1e6)个范围为 [ 1 , 1 e 9 ] [1,1\mathrm{e}9] [1,1e9]的整数,从中选出若干个整数,使得这些数中严格大于它们的平均值的数的个数最多,输出个数的最大值.
思路
将 n n n个数升序排列后,最优解选择的集合是一个前缀.
[证] 设最优解选择的集合的平均数不超过 a v g avg avg.
为使得平均数不超过 a v g avg avg,且严格 > a v g >avg >avg的数最多,则 ≤ a v g \leq avg ≤avg的数都应选,再贪心地选 > a v g >avg >avg的数中最小的若干个数.
将序列升序排列后枚举每个前缀,二分出其中 > a v g >avg >avg的数的位置,用其前面的数的个数更新答案.
代码 -> 2022CCPC浙江省赛-L(二分)
void solve() {
int n; cin >> n;
vi a(n);
for (int i = 0; i < n; i++) cin >> a[i];
sort(all(a));
int ans = 0;
double pre = 0; // 前缀和
for (int i = 0; i < n; i++) { // 枚举每个前缀
pre += a[i];
double avg = pre / (i + 1);
int l = 0, r = i;
while (l < r) {
int mid = l + r + 1 >> 1;
if (cmp(a[mid], avg) <= 0) l = mid; // a[mid]≤avg
else r = mid - 1;
}
ans = max(ans, i - r);
}
cout << ans;
}
int main() {
solve();
}
M. BpbBppbpBB
题意
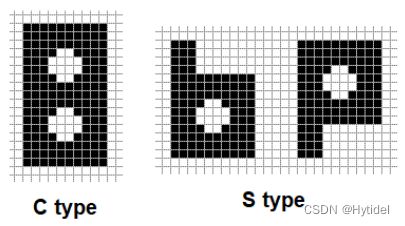
有如上图所示的两种印章,盖在纸上时可旋转 9 0 ∘ 90^\circ 90∘,两个印章可相邻,但不能重叠.给定一个 n × m ( 1 ≤ n , m ≤ 1000 ) n\times m\ \ (1\leq n,m\leq 1000) n×m (1≤n,m≤1000)的字符矩阵描述盖印后的纸,其中’#‘表示黑格子,’.'表示白格子.分别求C型、S型印章的使用次数.
思路
C型印章的黑格子数为 146 146 146,S型印章的黑格子数为 100 100 100.
设C型、S型印章分别用了 x x x、 y y y个.因印章不重叠,则黑格子数为 146 x + 100 y 146x+100y 146x+100y,洞数为 2 x + y 2x+y 2x+y,联立解出 x x x和 y y y即可.
此处不使用白格子数列方程是因为纸上未盖印的部分也是白格子.
考虑如何统计洞数.从上往下、从左往右扫一遍字符矩阵,遇到白格子时做一遍DFS,统计每个连通块中白格子的个数,若为 12 12 12,检查该白格子的附近是否满足洞的特征.
代码 -> 2022CCPC浙江省赛-M(Flood Fill)
const int MAXN = 1005;
int n, m;
string graph[MAXN];
bool vis[MAXN][MAXN]; // 记录每个格子是否已遍历过
void dfs(int x, int y, int& white) { // 统计每个连通块中白格子的个数
white++;
vis[x][y] = true;
for (int i = 0; i < 4; i++) {
int curx = x + dx[i], cury = y + dy[i];
if (curx < 0 || curx >= n || cury < 0 || cury >= m || graph[curx][cury] == '#') continue;
if (!vis[curx][cury]) dfs(curx, cury, white);
}
}
bool check(int x, int y) { // 检查白格子所在的连通块是否是洞:(x,y)为洞的第一行第一个白格子
if (y < 4) return false;
if (graph[x][y + 1] == '.' // 第一行
&& graph[x + 1][y - 1] == '.' && graph[x + 1][y] == '.' && graph[x + 1][y + 1] == '.' && graph[x + 1][y + 2] == '.' // 第二行
&& graph[x + 2][y - 1] == '.' && graph[x + 2][y] == '.' && graph[x + 2][y + 1] == '.' && graph[x + 2][y + 2] == '.' // 第三行
&& graph[x + 3][y] == '.' && graph[x + 3][y + 1] == '.') return true; // 第四行
else return false;
}
void solve() {
cin >> n >> m;
for (int i = 0; i < n; i++) cin >> graph[i];
int black = 0, hole = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (graph[i][j] == '#') black++;
else { // 白格子
if (!vis[i][j]) {
int white = 0;
dfs(i, j, white);
if (white == 12) hole += check(i, j);
}
}
}
}
cout << (100 * hole - black) / 54 << ' ' << hole - (100 * hole - black) / 27;
}
int main() {
solve();
}
G. Easy Glide
题意
在二维平面上,玩家可以 v 1 m / s v_1\ \mathrm{m/s} v1 m/s的速度行走.当玩家到达滑行点时,可以 v 2 m / s ( v 2 > v 1 ) v_2\ \mathrm{m/s}\ \ (v_2>v_1) v2 m/s (v2>v1)的速度滑行 3 s 3\ \mathrm{s} 3 s.给定起点 S S S、终点 T T T和途中的 n n n个滑行点 p 1 , ⋯ , p n p_1,\cdots,p_n p1,⋯,pn的坐标,求 S S S到 T T T的最短时间.
第一行输入一个整数 n ( 1 ≤ n ≤ 1000 ) n\ \ (1\leq n\leq 1000) n (1≤n≤1000).接下来 n n n行每行输入两整数 x i , y i ( − 1 e 6 ≤ x i , y i ≤ 1 e 6 ) x_i,y_i\ \ (-1\mathrm{e}6\leq x_i,y_i\leq 1\mathrm{e}6) xi,yi (−1e6≤xi,yi≤1e6),表示滑行点 p i ( 1 ≤ i ≤ n ) p_i\ \ (1\leq i\leq n) pi (1≤i≤n)的坐标.接下来一行输入四个整数 S x , S y , T x , T y ( − 1 e 6 ≤ S x , S y , T x , T y ≤ 1 e 6 ) S_x,S_y,T_x,T_y\ \ (-1\mathrm{e}6\leq S_x,S_y,T_x,T_y\leq 1\mathrm{e}6) Sx,Sy,Tx,Ty (−1e6≤Sx,Sy,Tx,Ty≤1e6),分别表示起点 S S S和终点 T T T的坐标.最后一行输入两整数 v 1 , v 2 ( 1 ≤ v 1 , v 2 ≤ 1 e 6 ) v_1,v_2\ \ (1\leq v_1,v_2\leq 1\mathrm{e}6) v1,v2 (1≤v1,v2≤1e6),分别表示行走速度和滑行速度.
输出 S S S到 T T T的最短时间,误差不超过 1 e − 6 1\mathrm{e}-6 1e−6.
思路
起点向每个滑行点和终点连单向边,边权为 S S S以速度 v 1 v_1 v1走到该节点所需的最短时间.每个滑行点向其他滑行点和终点连单向边,边权为先以速度 v 2 v_2 v2滑行 3 s 3\ \mathrm{s} 3 s,再以速度 v 1 v_1 v1走到该节点所需的最短时间.用朴素Dijkstra算法求 S S S到 T T T的最短路.时间复杂度 O ( n 2 ) O(n^2) O(n2).
代码 -> 2022CCPC浙江省赛-G(最短路)
const int MAXN = 1005;
int n; // 节点数
pii points[MAXN]; // 起点、滑行点、终点
int v1, v2;
double w[MAXN][MAXN]; // 两点间的权值
double dis[MAXN];
bool vis[MAXN];
double get_dis1(pii& a, pii& b) { // 以速度v1行走的最短时间
return hypot(a.first - b.first, a.second - b.second) / v1;
}
double get_dis2(pii& a, pii& b) { // 先以速度v2行走,再以速度v1行走的最短时间
double d = hypot(a.first - b.first, a.second - b.second);
double maxdis = v2 * 3;
if (cmp(maxdis, d) >= 0) return d / v2;
else return 3 + (d - maxdis) / v1;
}
double dijkstra() {
memset(dis, 0x42, so(dis));
dis[0] = 0;
for (int i = 1; i <= n; i++) {
int tmp = -1;
for (int j = 0; j <= n; j++)
if (!vis[j] && (tmp == -1 || dis[tmp] > dis[j])) tmp = j;
vis[tmp] = true;
for (int j = 1; j <= n; j++) dis[j] = min(dis[j], dis[tmp] + w[tmp][j]);
}
return dis[n];
}
void solve() {
memset(w, INFF, so(w));
cin >> n;
for (int i = 1; i <= n; i++) cin >> points[i].first >> points[i].second;
n++;
cin >> points[0].first >> points[0].second >> points[n].first >> points[n].second;
cin >> v1 >> v2;
// 建图
for (int j = 1; j <= n; j++) // 起点向其他滑行点和终点连边
w[0][j] = get_dis1(points[0], points[j]);
for (int i = 1; i <= n; i++) { // 滑行点向其他滑行点和终点连边
for (int j = 1; j <= n; j++) {
if (i == j) continue;
w[i][j] = get_dis2(points[i], points[j]);
}
}
cout << fixed << setprecision(12) << dijkstra();
}
int main() {
solve();
}
I. Barbecue
题意
Putata和Budada在玩字符串游戏,Putata先手,两人都采取最优策略.每轮玩家可删除字符串的第一个或最后一个字母,若此时字符串为回文串,则他失败;否则将该字符串传给下一人.给定一长度为 n ( 1 ≤ n ≤ 1 e 6 ) n\ \ (1\leq n\leq 1\mathrm{e}6) n (1≤n≤1e6)的字符串 s t r str str(下标从 1 1 1开始)和 q ( 1 ≤ q ≤ 1 e 6 ) q\ \ (1\leq q\leq 1\mathrm{e}6) q (1≤q≤1e6)次询问,每次询问给定整数 l , r ( 1 ≤ l ≤ r ≤ n ) l,r\ \ (1\leq l\leq r\leq n) l,r (1≤l≤r≤n),表示以 s t r [ ] str[] str[]为游戏起始时的字符串.对每组询问,输出最后胜利的玩家.
思路
若初始串为回文串,则后手胜;否则每轮开始时玩家拿到的字符串都不是回文串.若此时玩家必败,即删除第一个或最后一个字符都会使得剩下的字符串是回文串,则此时的串只能形如 a b , a b a b , a b a b a b , ⋯ ab,abab,ababab,\cdots ab,abab,ababab,⋯,这表明必败态的长度是偶数,故谁胜只与起始串长度的奇偶有关.
若每次询问都用Manacher算法判断回文串,时间复杂度 O ( n q ) O(nq) O(nq),会TLE.考虑用字符串哈希 O ( n ) O(n) O(n)预处理,每次询问 O ( 1 ) O(1) O(1)查询,时间复杂度 O ( n + q ) O(n+q) O(n+q).
代码 -> 2022CCPC浙江省赛-I(字符串哈希)
const int MAXN = 1e6 + 5;
const int P = 13331;
int n, q; // 长度、询问次数
char str[MAXN];
ull ha[MAXN], rha[MAXN]; // str正着和反着的哈希值
ull Ppow[MAXN]; // P的乘方
ull get_hash(int l, int r) { // 求子串[l,r]正着的哈希
return ha[r] - ha[l - 1] * Ppow[r - l + 1];
}
ull get_rhash(int l, int r) { // 求子串[l,r]反着的哈希
return rha[n - l + 1] - rha[n - r] * Ppow[r - l + 1];
}
void init() { // 预处理出ha[]和rha[]
Ppow[0] = 1;
for (int i = 1; i <= n; i++) {
ha[i] = ha[i - 1] * P + str[i];
rha[i] = rha[i - 1] * P + str[n - i + 1];
Ppow[i] = Ppow[i - 1] * P;
}
}
void solve() {
cin >> n >> q >> str + 1;
init();
while (q--) {
int l,r; cin >> l >> r;
if (get_hash(l, r) == get_rhash(l, r)) cout << "Budada" << endl;
else {
int len = r - l + 1;
if (len & 1) cout << "Putata" << endl;
else cout << "Budada" << endl;
}
}
}
int main() {
solve();
}