2020年中国大学生程序设计竞赛(CCPC) - 网络选拔赛部分题解
前言
既培养算法知识,又能学习按摩手法,我们还有专业的算命大师帮你窥察天机。
这还犹豫什么,快来加入我们。前10名还能请大师免费帮你看风水,让你死后也能安心。

我怕不是进了一个人才市场…
Express Mail Taking(贪心)
比赛链接:https://acm.dingbacode.com/showproblem.php?pid=6890
题目大意
上头给你分配一个任务:取回丢失的文件。
出发点为 x = 1 x=1 x=1处,m个文件被分散在坐标轴上各处,第i个文件被锁在了 x = a i x=a_i x=ai的位置。
如果你想取出处于 x = i x=i x=i位置的文件,你需要先去 x = k x=k x=k处输入密码,然后去 x = i x=i x=i处取出文件。
在你取完所有文件之后回到 x = 1 x=1 x=1处即算任务完成。
问:你最少需要移动的距离。
思路
正常的文件取回过程:
当前位置 → x = k x=k x=k处 → 接下来要取的文件位置 → x = k x=k x=k处 → …
最后一个文件的取回过程:
当前位置 → x = k x=k x=k处 → 最后一个文件的位置 → x = 1 x=1 x=1处
我们会发现,只有最后一个文件的位置会改变我们的移动距离(中间过程的值不会改变的)。
所以我们需要让最后取的那份文件离 x = 1 x=1 x=1越近越好。
其次就是从 x = 1 x=1 x=1移动到 x = 5 x=5 x=5需要走 4 ( 5 − 1 ) 4(5-1) 4(5−1)步。
(一开始在这里卡住了,我是废物)
AC代码
#includeCCPC Training Class(水题+技高一筹)
比赛链接:https://acm.dingbacode.com/showproblem.php?pid=6894
题目大意
给出字符串 s s s,求出字符串 s s s中字符出现次数的最大值 W W W。
思路
别看我啊,真的,这题目这么长实际上就是求个最大出现次数。
就挺离谱的,中间还有三个数学公式,一开始看到的时候没给爷吓死。
幸亏我技(lao)高(jian)一(ju)筹(hua),看了看样例,盲猜一波就过了。

实际上我们把题目中给出的公式倒推一下,确实就是字符出现次数的最大值。
AC代码
#includeReports(水题)
比赛链接:https://acm.dingbacode.com/showproblem.php?pid=6897
题目大意
由于新冠疫情原因,Kanade每次进出学校都需要提交一份核酸检测报告。
Kanade的核酸检测报告序列由 0 0 0与 1 1 1组成, 0 0 0代表的是离校时的核酸检测报告, 1 1 1代表的是进校时的核酸检测报告。
一个人的核酸检测报告序列当且仅当不存在两个连续且性质相同的报告时才算是一份合格的核酸检测报告序列。
请问Kanade的核酸检测报告序列是否合格。
思路
就是判断字符串中是否含有00或是11,怎么写都可以。
AC代码
#include3x3 Convolution(规律+数学)
比赛链接:https://acm.dingbacode.com/showproblem.php?pid=6898
题目大意
给定大小为 n ∗ n n*n n∗n的矩阵 A A A与大小为 3 ∗ 3 3*3 3∗3的矩阵 K ′ K' K′。
首先按照公式求出大小为 3 ∗ 3 3*3 3∗3的矩阵 K K K: K i , j = K i , j ′ / ( ∑ x = 1 3 ∑ y = 1 3 K x , y ′ ) K_{i,j}=K'_{i,j}/(\sum_{x=1}^{3}\sum_{y=1}^{3}K'_{x,y}) Ki,j=Ki,j′/(∑x=13∑y=13Kx,y′)。
接下来定义函数 C ( A , K ) C(A,K) C(A,K),函数 C ( A , K ) C(A,K) C(A,K)的返回值为大小为 n ∗ n n*n n∗n的矩阵 C C C:
C x , y = ∑ i = 1 m i n ( n − x + 1 , 3 ) ∑ j = 1 m i n ( n − y + 1 , 3 ) A x + i − 1 , y + j − 1 K i , j C_{x,y}=\sum_{i=1}^{min(n-x+1,3)}\sum_{j=1}^{min(n-y+1,3)}A_{x+i-1,y+j-1}K_{i,j} Cx,y=∑i=1min(n−x+1,3)∑j=1min(n−y+1,3)Ax+i−1,y+j−1Ki,j
紧接着定义 C m ( A , K ) = C ( C m − 1 ( A , K ) , K ) C^m(A,K)=C(C^{m-1}(A,K),K) Cm(A,K)=C(Cm−1(A,K),K), C 1 ( A , K ) = C ( A , K ) C^1(A,K)=C(A,K) C1(A,K)=C(A,K)。
请输出 lim t → ∞ C t ( A , K ) \lim_{t\rightarrow \infty} {C^t(A,K)} limt→∞Ct(A,K)的结果。
思路
千万不要被题目所吓倒,菜狗博主都能看懂的东西,没你想的那么复杂。
这题也是可以猜的,只要胆子大,5min交3发。
但我们最好还是要明白为啥答案是那样的。
首先我们先看矩阵K的特点。
根据题目中的公式 K i , j = K i , j ′ / ( ∑ x = 1 3 ∑ y = 1 3 K x , y ′ ) K_{i,j}=K'_{i,j}/(\sum_{x=1}^{3}\sum_{y=1}^{3}K'_{x,y}) Ki,j=Ki,j′/(∑x=13∑y=13Kx,y′)我们可以推断出:
1.矩阵 K K K中的值 K i , j K_{i,j} Ki,j的大小范围为 [ 0 , 1 ] [0,1] [0,1]。而且只有当矩阵 K ′ K' K′中只有一个非 0 0 0数时,矩阵 K K K中才会有一个 1 1 1。此时矩阵 K K K除去这个 1 1 1之后剩下的位置一定都是 0 0 0。
接下来我们再看一下函数 C ( A , K ) C(A,K) C(A,K)。
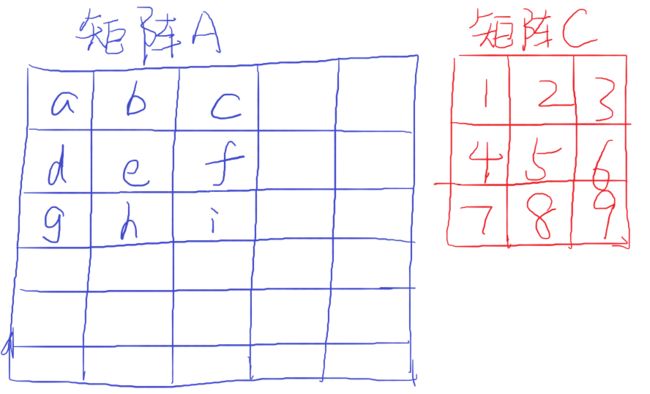
根据公式 C x , y = ∑ i = 1 m i n ( n − x + 1 , 3 ) ∑ j = 1 m i n ( n − y + 1 , 3 ) A x + i − 1 , y + j − 1 K i , j C_{x,y}=\sum_{i=1}^{min(n-x+1,3)}\sum_{j=1}^{min(n-y+1,3)}A_{x+i-1,y+j-1}K_{i,j} Cx,y=∑i=1min(n−x+1,3)∑j=1min(n−y+1,3)Ax+i−1,y+j−1Ki,j以及博主画的图(较丑,多多包含)可以推断出:
C 1 , 1 = a ∗ 1 + b ∗ 2 + c ∗ 3 + d ∗ 4 + e ∗ 5 + f ∗ 6 + g ∗ 7 + h ∗ 8 + i ∗ 9 C_{1,1}=a*1+b*2+c*3+d*4+e*5+f*6+g*7+h*8+i*9 C1,1=a∗1+b∗2+c∗3+d∗4+e∗5+f∗6+g∗7+h∗8+i∗9
从 C 1 , 1 C_{1,1} C1,1的推导式中我们不难看出:
- 如果 1 1 1 ~ 9 9 9中所有位置上的数字都小于 1 1 1,则在求极限的过程中会让 C 1 , 1 C_{1,1} C1,1越来越小,最后变成0;
- 不让 C 1 , 1 C_{1,1} C1,1变小的情况只有一种: 1 1 1 ~ 9 9 9中有一个位置上的数是 1 1 1。
但这种情况我们也分析了:一旦有 1 1 1 ~ 9 9 9中有一个数是 1 1 1,则说明矩阵 K K K中只有一个位置是 1 1 1,其他位置都是 0 0 0。
那么我们就得观察以下这个 1 1 1存在于矩阵 K K K的每个位置上时对答案的影响,于是博主设计了一个代码:
#include在这里,矩阵A是一个3*3的数组,内容为:
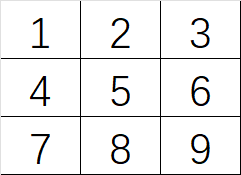
虽然有点小但是符合题目条件。
博主模拟了整个过程,每次改变矩阵 K K K中1的位置并输出 m = 1 m=1 m=1~ 10 10 10的的所有 C m ( A , K ) C^m(A,K) Cm(A,K)。
观察结果,我们会发现:
2.当这个 1 1 1在 ( 1 , 1 ) (1,1) (1,1)位置的时候 C m ( A , K ) C^m(A,K) Cm(A,K)恒等于矩阵 A A A。而当 1 1 1在矩阵 K K K的其他位置时,随着 m m m的增大, C m ( A , K ) C^m(A,K) Cm(A,K)的值趋近于一个全零矩阵。
仔细观察这个过程会发现,当 1 1 1在矩阵 K K K的其他位置时,每一次求 C ( A , K ) C(A,K) C(A,K)之后,所有的值都会向着 ( 1 , 1 ) (1,1) (1,1)点靠近,最后变成0。
博主比较菜,不太会解释这个地方,但是这种方式应该也能帮大家接受第2条结论。
有兴趣的朋友自行寻找大佬吧,博主只是个笑话而已。
AC代码
#include后话
感谢阅读,希望能对你产生一点用处。
以下台词取自《银魂》第103集:
(真选组的灵魂:『猩猩追踪狂』近藤勋+『蛋黄酱狂魔』土方十四郎+『超级抖S』冲田总悟+『红豆包天使』山崎退)
![]()