【LeetCode】错误的集合&&在排序数组中查找元素的第一个和最后一个位置&&杨氏矩阵&&寻找数组的中心下标&&两个数组的交集
作者:@阿亮joy.
专栏:《阿亮爱刷题》
座右铭:每个优秀的人都有一段沉默的时光,那段时光是付出了很多努力却得不到结果的日子,我们把它叫做扎根
目录
-
- 错误的集合
-
- 思路一
- 思路二
- 在排序数组中查找元素的第一个和最后一个位置
- 排序矩阵查找
- 寻找数组的中心下标
- 两个数组的交集
- 总结
错误的集合
集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合丢失了一个数字并且有一个数字重复 。
给定一个数组 nums 代表了集合 S 发生错误后的结果。
请你找出重复出现的整数,再找到丢失的整数,将它们以数组的形式返回。
示例 1:
输入:
nums = [1,2,2,4]
输出:[2,3]
示例 2:
输入:
nums = [1,1]
输出:[1,2]
提示:
- 2 <= nums.length <= 10^4
- 1 <= nums[i] <= 10^4
思路一
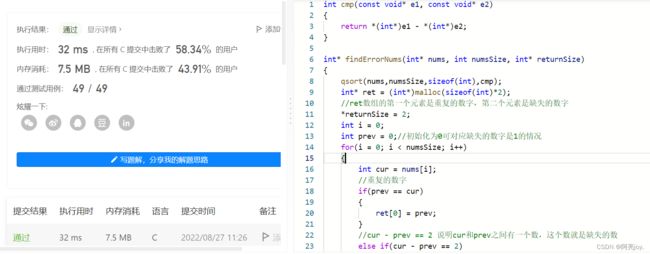
首先对数组进行快排,然后定义两个两个变量prev和cur,prev初始化为0可对应缺失的数字是1的情况。cur是当前的数组元素,prev是当前的数组元素的上一个元素。当prev == cur时,说明重复的数字为prev;当cur - prev == 2时,说明prev和cur之间还有一个数字,该数字就是缺失的数字prev + 1。当for循环结束时,需要判断nums[numsSize - 1]是否等于numsSize。如果不等,说明缺失的数字为numsSize。
int cmp(const void* e1, const void* e2)
{
return *(int*)e1 - *(int*)e2;
}
int* findErrorNums(int* nums, int numsSize, int* returnSize)
{
qsort(nums,numsSize,sizeof(int),cmp);
int* ret = (int*)malloc(sizeof(int)*2);
//ret数组的第一个元素是重复的数字,第二个元素是缺失的数字
*returnSize = 2;
int i = 0;
int prev = 0;//初始化为0可对应缺失的数字是1的情况
for(i = 0; i < numsSize; i++)
{
int cur = nums[i];
//重复的数字
if(prev == cur)
{
ret[0] = prev;
}
//cur - prev == 2 说明cur和prev之间有一个数,这个数就是缺失的数
else if(cur - prev == 2)
{
ret[1] = prev + 1;
}
prev = cur;
}
//缺失的数字是numsSize
if(nums[numsSize-1] != numsSize)
{
ret[1] = numsSize;
}
return ret;
}
思路二
遍历nums数组,将其中数据对应的位置1, 哪一位如果已经重置过则意味着数据重复了,该数据就是重复的数字。在遍历数组的同时,求出1到 numsSize 的和oddSum以及nums数组的和curSum。因为nums数组多了一个重复的数字,少了一个缺失的数字,所以oddSum加上重复的数字ret[0]再减去curSum得到的就是消失的数字了。
int* findErrorNums(int* nums, int numsSize, int* returnSize)
{
//遍历nums数组,将其中数据对应的位置1, 哪一位如果已经重置过则意味着数据重复了
int* arr = (int*)calloc(numsSize+1, sizeof(int));//申请numsSize+1个整形空间,并初始化为0
//申请numsSize+1个整型空间是防止数组越界
int* ret = (int*)calloc(2, sizeof(int));//申请2个整形空间,并初始化为0
*returnSize = 2;
int oddSum = 0;//记录1到numsSize的和
int curSum = 0;//记录当前数组的和
int i = 0;
for(i = 0;i < numsSize; i++)
{
if(arr[nums[i]] == 1)//nums[i]这个数字在arr数组的对应位置已经置过1了,则重复
{
ret[0] = nums[i];
}
arr[nums[i]] = 1;//将标记数组的对应数据位置1
oddSum += i+1;//1到numsSize的求和
curSum += nums[i];//当前数组中的数据求和(多了一个重复的,少了一个丢失的)
}
ret[1] = oddSum + ret[0] - curSum;//原始总和加上重复的数字再减去当前总和就得到消失的数字
free(arr);
return ret;
}
在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:
nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:
nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
提示:
- 0 <= nums.length <= 105
- -10^9 <= nums[i] <= 10^9
- nums 是一个非递减数组
- -10^9 <= target <= 10^9
思路:先定义一个找target左边界的函数,然后利用这个函数找target + 1的左边界,target + 1的左边界减去1就相当于target的右边界。定义first为target的左边界,当frist == numsSize或者nums[frist] != target时,就说明数组中没有target。
//寻找target的左边界,该函数也可以寻找target的右边界
int binarySearch(int* nums,int numsSize,int target)
{
int left=0;
int right=numsSize-1;
while(left<=right)
{
int mid=left+(right-left)/2;
if(nums[mid]<target)
{
left=mid+1;
}
else if(nums[mid]>=target)
{
right=mid-1;
}
}
return left;
}
int* searchRange(int* nums, int numsSize, int target, int* returnSize)
{
int first=binarySearch(nums,numsSize,target);//target的左边界
int last=binarySearch(nums,numsSize,target+1);//target+1的左边界
int* result=(int*)malloc(sizeof(int)*2);
*returnSize=2;
//当first==numsSize时,说明target大于数组的最后一个元素
//当nums[first]!=target,说明数组中没有target
if(first==numsSize||nums[first]!=target)
{
result[0]=-1;
result[1]=-1;
return result;
}
else
{
result[0]=first;
result[1]=last-1;//last-1为target1的右边界
return result;
}
}
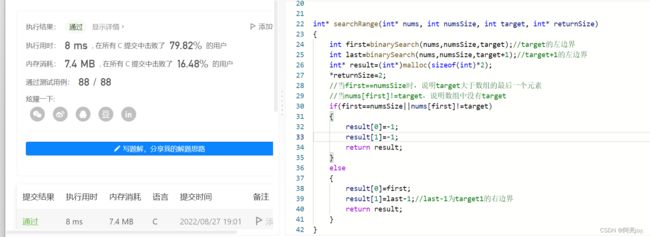
注意:当first == numsSize或者nums[frist] != target时,target在数组中出现了0次。如果不符合以上情况,那么数组中就含有target,last - first就是target在数组中出现的次数。
排序矩阵查找
给定M×N矩阵,每一行、每一列都按升序排列,请编写代码找出某元素。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30].
]
给定 target = 5,返回true。
给定 target = 20,返回 false。
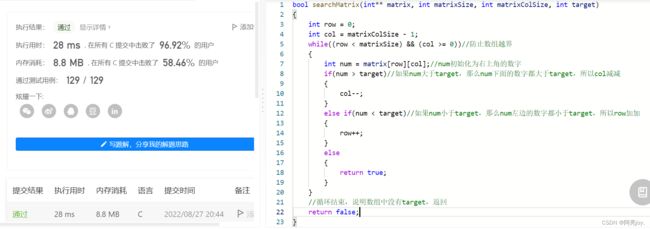
思路:这道题目最容易想到的解法应该就是遍历整个二维数组,如果数组中出现了target,就返回true;否则,返回false。但是这种解法并没有利用到杨氏矩阵的特点:每一行、每一列的数字都按升序排列,时间复杂度为O(row * col)。还有另一种更加高效的解法,先定义两个变量row和col,row初始化为0,col初始化为matrixColSize。再定义一个变量num= matrix[row][col],如果num大于target,那么num下面的数字都大于target,所以col减减;如果num小于target,那么num左边的数字都小于target,所以row加加。如果num等于target,就返回true。如果循环结束了,说明数组中没有target,返回false。这种解法一次查找能够排查一行或者一列的数字,时间复杂度为O(row + col)。
注意:因为num初始化为右上角的数字,所以num只能向左方和下方移动。也就是说row只能加加,不能减减;col只能减减,不能加加。不过num也可以初始化为左下角的数字,那么移动方向就相反了。

bool searchMatrix(int** matrix, int matrixSize, int matrixColSize, int target)
{
int row = 0;
int col = matrixColSize - 1;
while((row < matrixSize) && (col >= 0))//防止数组越界
{
int num = matrix[row][col];//num初始化为右上角的数字
if(num > target)//如果num大于target,那么num下面的数字都大于target,所以col减减
{
col--;
}
else if(num < target)//如果num小于target,那么num左边的数字都小于target,所以row加加
{
row++;
}
else
{
return true;
}
}
//循环结束,说明数组中没有target,返回
return false;
}
寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组中心下标是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:
nums = [1, 7, 3, 6, 5, 6]
输出:3
解释: 中心下标是 3 。 左侧数之和sum = nums[0] +nums[1] + nums[2] = 1 + 7 + 3 = 11, 右侧数之和sum = nums[4] + nums[5] = 5+ 6 = 11,二者相等。
示例 2:
输入:
nums = [1, 2, 3]
输出:-1
解释: 数组中不存在满足此条件的中心下标。
示例 3:
输入:
nums = [2, 1, -1]
输出:0
解释: 中心下标是 0 。 左侧数之和sum = 0,(下标 0 左侧不存在元素),
右侧数之和sum = nums[1] + nums[2] = 1 + -1 = 0。
提示:
- 1 <= nums.length <= 10^4
- -1000 <= nums[i] <= 1000
思路:先遍历一次数组,求出数组的和sum。再遍历一次数组求出数组左边的和sum1与右边的和sum2,比较sum1和sum2是否相等。若相等,就返回下标i;若for循环结束,表明没有中心下标,返回 -1。

int pivotIndex(int* nums, int numsSize)
{
int sum=0;
int i=0;
for(i=0;i<numsSize;i++)
{
sum+=nums[i];
}
int sum1=0;//左边的和
int sum2=0;//右边的和
for(i=0;i<numsSize;i++)
{
//nums[i]为中间的数,左和和右和同时加上不影响结果
sum1+=nums[i];
sum2=sum-sum1+nums[i];
if(sum1==sum2)
{
return i;
}
}
return -1;
}
两个数组的交集
给定两个数组 nums1 和 nums2 ,返回它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
示例 1:
输入:
nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
输入:
nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的
提示:
- 1 <= nums1.length, nums2.length <= 1000
- 0 <= nums1[i], nums2[i] <= 1000
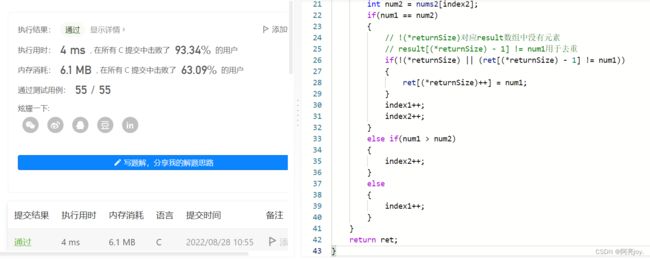
思路:先对两个数组进行快速排序,然后定义两个变量index1和index2。当nums1[index1] == nums2[index2]时,需要判断返回的数组是否为空。如果为空,nums1[index1]直接放入返回的数组中;如果不为空,就需要判断数组前一个元素是否等于nums1[index1],如果不等于就将nums1[index1]放入返回的数组中。如果nums1[index1]和nums2[index2]不相等,且nums[index1]小,则index1++;反之,index2++。
int cmp(const void* a, const void* b)
{
return *(int*)a - *(int*)b;
}
int* intersection(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize)
{
//先排序
qsort(nums1,nums1Size,sizeof(int),cmp);
qsort(nums2,nums2Size,sizeof(int),cmp);
//返回数组的最大长度是nums1Size或者nums2Size
int max = nums1Size > nums2Size ? nums1Size : nums2Size;
int* ret = (int*)malloc(sizeof(int)*max);
//后利用双指针寻找交集
int index1 = 0;
int index2 = 0;
*returnSize = 0;
while((index1 < nums1Size) && (index2 < nums2Size))
{
int num1 = nums1[index1];
int num2 = nums2[index2];
if(num1 == num2)
{
// !(*returnSize)对应result数组中没有元素
// result[(*returnSize) - 1] != num1用于去重
if(!(*returnSize) || (ret[(*returnSize) - 1] != num1))
{
ret[(*returnSize)++] = num1;
}
index1++;
index2++;
}
else if(num1 > num2)
{
index2++;
}
else
{
index1++;
}
}
return ret;
}
总结
本篇博客讲解了几道数组的题目,其中涉及到二分查找算法、在杨氏矩阵查找一个数字和双指针的思想,希望大家能够理解掌握。如果大家觉得有收获的话,可以点个三连支持一下!谢谢大家啦!❣️