【数据结构与算法】BF算法、KMP算法及OJ题

作者：@阿亮joy.
专栏：《数据结构与算法要啸着学》
座右铭：每个优秀的人都有一段沉默的时光，那段时光是付出了很多努力却得不到结果的日子，我们把它叫做扎根

引言

字符串匹配就是在主串str中查找子串sub（也称为模式串），看子串sub是否在主串str中。如果存在，就返回子串sub在第一次在主串str中出现的位置或者地址（指针）；如果不存在，就返回 -1 或者NULL。那么，我想有小伙伴就会问，如果子串sub为空字符串，函数的返回值是什么？库函数strstr的返回值是主串str的首元素地址。那么以下将要介绍的BF算法和KMP算法也和库函数strstr保持一致，即当子串sub为空字符串时，BK算法和KMP算法的返回值为 0（博主的BF算法和KMP的算法返回值为int，当然也可以设置为char*）。

在学习BF算法和KMP算法之前呢，我们来看一下库函数strstr的源码和模拟实现库函数strstr。

库函数strstr的源码

strstr的函数原型：

char * strstr ( const char *str1, const char * str2);

char* __cdecl strstr(const char* str1,const char* str2)
{
    char* cp = (char*)str1;
    char* s1, * s2;

    if (!*str2)
        return((char*)str1);

    while (*cp)
    {
        s1 = cp;
        s2 = (char*)str2;

        while (*s2 && !(*s1 - *s2))
            s1++, s2++;

        if (!*s2)
            return(cp);

        cp++;
    }

    return(NULL);

}

上面就是库函数strstr的源码了，那这代码是什么意思呢？现在就带着大家学习一下（见下图）。希望大家可以将下图仔细地看一下，写得非常的详细。

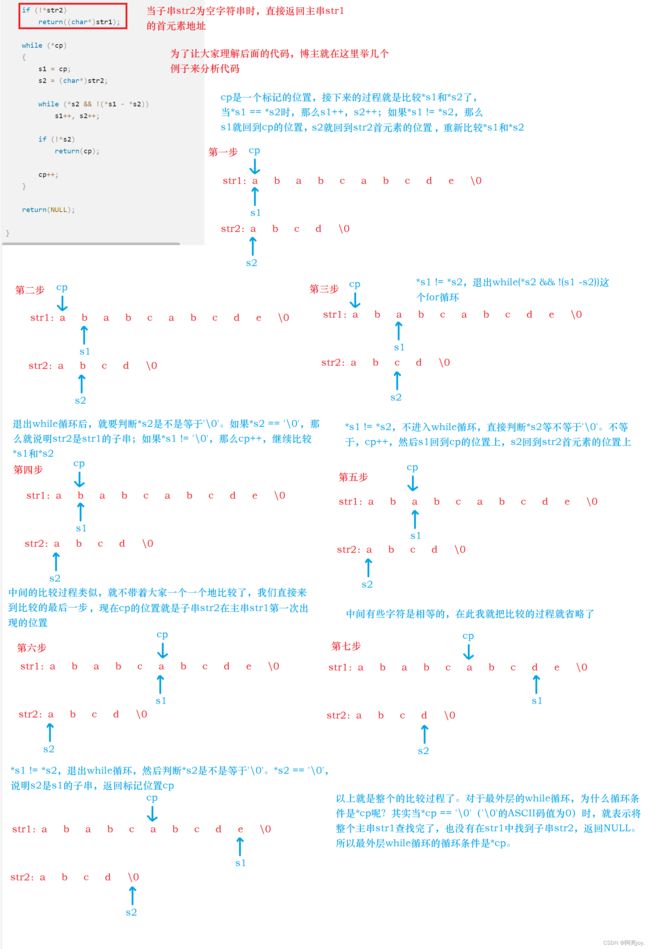
以上就是库函数strstr的实现逻辑和图解了。其实库函数strstr的可读性较差，同时还没有对传进来的str1和str2进行判断为不为NULL，健壮性较差。所以，我们就模拟实现库函数strstr。

模拟实现库函数strstr

//模拟实现库函数strstr
//my_strstr不会修改str和sub的内容，所以用const修饰str和sub，增强代码的健壮性
//str：主串   sub：子串
#include 
#include 
char* my_strstr(const char* str, const char* sub)
{
	//对str和sub进行是否等于NULL判断
	assert(str != NULL && sub != NULL);
	//sub为空字符串，直接返回str
	if (*sub == '\0')
	{
		return str;
	}

	const char* s1 = NULL;//遍历主串str
	const char* s2 = NULL;//遍历子串sub
	const char* mark = str;//标记位置
	while (*mark)
	{
		//回溯
		s1 = mark;
		s2 = sub;
		while (*s1 && *s2 && (*s1 == *s2))
		{
			s1++;
			s2++;
		}
		//如果*s2 == '\0'，说明sub是str的子串，返回mark
		//反之，则mark++，继续查找
		if (*s2 == '\0')
		{
			return (char*)mark;
		}
		mark++;
	}
	//sub不是str的子串，返回NULL
	return NULL;
}

int main()
{
	char str[] = "ababcabcde";
	char sub[] = "abcd";
	char* ret = my_strstr(str, sub);
	printf("%s\n", ret);
	return 0;
}

其实，不管是库函数strstr还是自定义函数my_strstr的算法思想就是BF算法思想。那BF算法是什么呢？接下来，我们来学习一下。

BF算法

BF算法，即暴力(Brute Force)算法，是普通的模式匹配算法，BF算法的思想就是将目标串str的第一个字符与模式串sub的第一个字符进行匹配，若相等，则继续比较str的第二个字符和sub的第二个字符；若不相等，则比较str的第二个字符和sub的第一个字符，依次比较下去，直到得出最后的匹配结果。BF算法是一种暴力算法。

看完BF算法的定义，我们就可以发现库函数strstr和自定义函数my_strstr的算法都是BF算法，是一种暴力的算法。

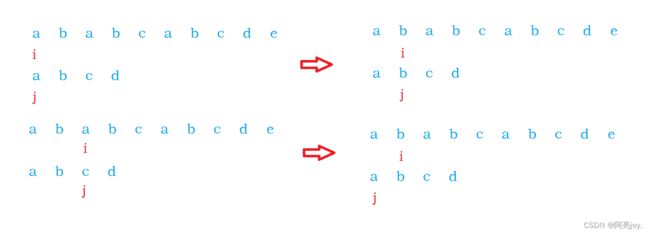
博主再借助上面的例子给大家讲解一下BF算法。假定我们给出字符串 ”ababcabcdabcde”作为主串， 然后给出子串 ”abcd”,现在我们需要查找子串是否在主串中
出现，出现就返回主串中的第一个匹配的下标，没有出现则返回 -1。

只要在匹配的过程当中，匹配失败，那么，i 回退（或者回溯）到刚刚位置的下一个，j 回退到 0 下标重新开始。如此反复，直到最终找到或者找不到。

BF算法的核心

BF算法的核心操作就是回溯。当str[i] != sub[j]时，那么，i 回溯到刚刚位置的下一个，j 回溯到 0 下标重新开始。j 的回溯到 0 比较简单，那 i 的回溯可以借助一个临时变量mark来记住。当然，i 也有有个回溯公式i = i - j + 1。因为 i 和 j 都是每次自增都是自增一的，所以才会有这个回溯公式，大家可以通过上面的例子来验证一下。在此，就不再进行证明了。

BF算法代码实现

#include 
#include 
#include 
//str: 主串    sub: 子串
//返回值:返回子串在主串中第一次出现的下标，没有出现则返回-1
//sub为空字符串时，返回0(与库函数strstr保持一致)
int BF(const char* str, const char* sub)
{
	//判断str和sub是不是NULL
	assert(str && sub);
	int strLen = strlen(str);
	int subLen = strlen(sub);
	//sub为空字符串的情况
	if (subLen == 0)	return 0;
	//主串长度小于子串长度的情况
	if (strLen < subLen)	return -1;
	//上面的主串长度小于子串长度情况会包含在while循环中
	//对这种情况进行单独处理，不用进入while循环
	int i = 0;
	int j = 0;
	while (i < strLen && j < subLen)
	{
		if (str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			//回溯
			i = i - j + 1;
			j = 0;
		}
	}
	if (j == subLen)//j走完了子串sub，找到了
	{
		return i - j;
	}
	return -1;//没找到子串sub
}

int main()
{
	printf("%d\n", BF("ababcabcdabcde", "abcd"));//5
	printf("%d\n", BF("ababcabcde", "abcdf"));//-1
	printf("%d\n", BF("ababcabcde", "ab"));//0
	printf("%d\n", BF("ababcabcde", "\0"));//0
	printf("%d\n", BF("\0", "a"));//-1

	return 0;
}

时间复杂度分析：最坏情况为O(m*n)；m 是主串长度，n 是子串长度。

KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next数组实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)。

KMP算法和BF算法最大的区别就是：当str[i] != sub[j]时，i 并不会回退，并且 j 回退到特定位置（由next数组决定）。这就是KMP算法比BF算法高效的原因所在了。

为什么 i 可以不回退？

j 的回退位置

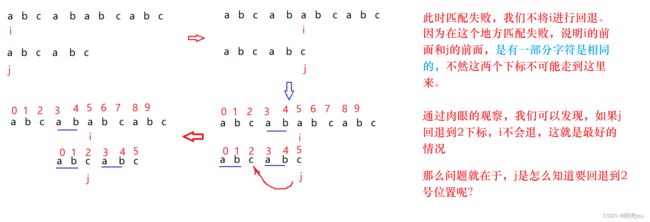
其实 j 回退的位置就是 j 前面的字符串的最长相同前后缀的长度，而next数组中存储的就是当前 j 位置前面的字符串的最长相同前后缀的长度。那最长相同前后缀是什么呢？我们现在来学习一下。

最长相同前后缀

现在博主给出一个例子，大家可以看一下。相信聪明的大家，一定能够看懂。

字符串 "abcdab"
前缀的集合：{"a","ab","abc","abcd","abcda"}
后缀的集合：{"b","ab","dab","cdab","bcdab"}
注意：前后缀的集合要求为非空真子集。

那么，最长相同前后缀就是"ab"，其长度为 2。这个概念非常地重要，希望大家能够掌握。因为next数组存储的信息就是 j 位置前的字符串的相同前后缀的最大长度。当str[i] != sub[j]时，j 回退的位置就是next[j]。

其实通过肉眼观察，很容易就可以知道一个字符串的相同前后缀的最大长度。但是，如何用代码来求取子串sub的每个位置的相同前后缀的最大长度呢？接下来，我们就来学习next数组的引入。

next 数组的引入

KMP算法的精髓就是next数组：也就是用next[j] = K来表示，不同的 j 来对应一个 K 值。当str[i] != sub[j]时，此时 j 就要回退到下标为 K的位置。

K值求取的规则

1、规则：找到匹配成功部分的两个相等的真子串（不包含本身），一个以下标 0 字符开始，另一个以 j-1 下标 字符结尾。
2、不管什么数据，next[0] = -1,next[1] = 0;在这里，我们以下标来开始，而说到的第几个第几个是从 1 开始。

求next数组的练习

练习 1： 对于字符串”ababcabcdabcde”， 求其的 next 数组？
练习2： 对于字符串”abcabcabcabcdabcde”，求其的 next 数组？

这两道练习就是考察对最长相同前后缀概念的理解，如果还是不懂的话，再看多几次最长相同前后缀的概念。下图是两道练习题的答案：

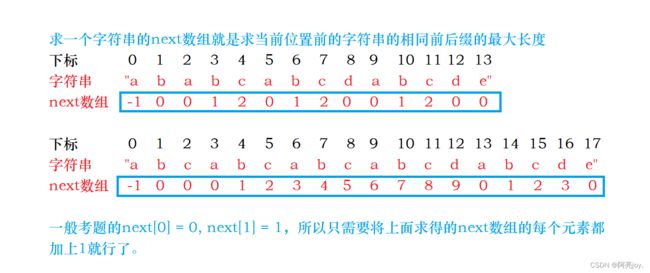
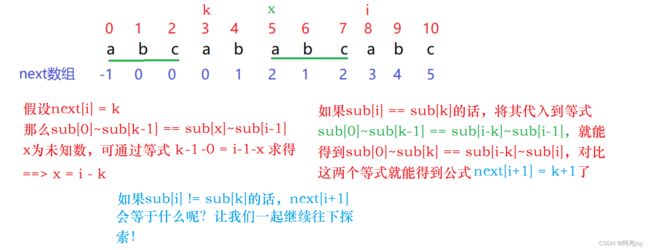
到这里，相信大家对如何求next数组应该问题不大了。接下来的问题就是，已知next[i] = k，怎么求next[i+1] = ?如果我们能够通过next[i]的值,通过公式转换得到next[i+1]的值，那么我们就能够通过代码实现这部分。那么其中公式怎么来的呢？见下图证明：

KMP算法代码实现

#include 
#include 
#include 
#include 
void GetNext(char* sub, int* next, int subLen)
{
	next[0] = -1;
	if (subLen == 1)
	{
		return;
	}

	next[1] = 0;
	int i = 2;//当前的i下标
	int k = 0;//前一项的k
	while (i < subLen)
	{
		if (k == -1 || sub[i - 1] == sub[k])
		{
			next[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = next[k];
		}
	}
}
//str:主串
//sub:子串
//pos:从主串的pos位置开始找
int KMP1(const char* str, const char* sub, int pos)
{
	assert(str && sub);
	int strLen = strlen(str);
	int subLen = strlen(sub);
	if (subLen == 0)	return 0;
	if (strLen < subLen)	return -1;
	if (pos < 0 || pos >= strLen)	return -1;

	int* next = (int*)malloc(sizeof(int) * subLen);
	assert(next);
	//引入next数组
	GetNext(sub, next, subLen);
	
	int i = pos;//遍历主串
	int j = 0;//遍历子串
	while (i < strLen && j < subLen)
	{
		if (j == -1 || str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			j = next[j];
		}
	}
	if (j == subLen)
	{
		free(next);
		next = NULL;
		return i - j;
	}
	else
	{
		free(next);
		next = NULL;
		return -1;
	}
}

int main()
{
	printf("%d\n", KMP1("ababcabcde", "abcd", 0));//5
	printf("%d\n", KMP1("ababcabcde", "abcdf", 0));//-1
	printf("%d\n", KMP1("ababcabcde", "ab", 0));//0
	printf("%d\n", KMP1("ababcabcde", "a", 0));//0
	printf("%d\n", KMP1("ababcabcde", "a", -1));//-1
	printf("%d\n", KMP1("ababcabcde", "a", 11));//-1
	printf("%d\n", KMP1("\0", "a", 0));//-1

	return 0;
}

next数组的优化

next数组的优化，即如何得到nextval数组。
字符串： "aaaaaaaab"
next数组：[-1 0 1 2 3 4 5 6 7]
nextval数组： [-1 -1 -1 -1 -1 -1 -1 -1 7]

为什么出现修正后的数组，假设在 5 号位置匹配失败了，那退一步还是字符 a，还是匹配失败，接着退还是 字符 a。

那么如何对next数组来进行优化呢？

为了让大家熟悉next数组的优化，请大家完成下面的练习。

练习：模式串 t= “abcaabbcabcaabdab” ，该模式串的 next 数组的值为（ ） ， nextval 数组的值为 （）。
A． 0 1 1 1 2 2 1 1 1 2 3 4 5 6 7 1 2
B． 0 1 1 1 2 1 2 1 1 2 3 4 5 6 1 1 2
C． 0 1 1 1 0 0 1 3 1 0 1 1 0 0 7 0 1
D． 0 1 1 1 2 2 3 1 1 2 3 4 5 6 7 1 2
E． 0 1 1 0 0 1 1 1 0 1 1 0 0 1 7 0 1
F． 0 1 1 0 2 1 3 1 0 1 1 0 2 1 7 0 1
答案：D和F，大家尝试做一下，做不出来再看下面的解析。

nextval 数组代码实现

#include 
#include 
#include 
#include 
//next数组的优化
//sub：子串
//str：主串
void NextVal(char* sub, int* nextval , int subLen)
{
	assert(sub);
	nextval[0] = -1;
	if (subLen == 1)
	{
		return;
	}

	nextval[1] = 0;
	int i = 2;//当前的i下标
	int k = 0;//前一项的k值
	//先将nextval数组初始化为next数组
	while (i < subLen)
	{
		if (k == -1 || sub[i - 1] == sub[k])
		{
			nextval[i] = k + 1;
			i++;
			k++;
		}
		else
		{
			k = nextval[k];
		}
	}
	//修改nextval数组
	i = 2;
	for (; i < subLen; i++)
	{
		//回退到的位置上的字符和当前i位置上的字符相等
		//nextval[i]为回退到的位置
		//sub[nextval[i]]为回退到的位置上的字符
		if (sub[i] == sub[nextval[i]])
		{
			nextval[i] = nextval[nextval[i]];
		}
	}
}

int KMP2(char* str, char* sub, int pos)
{
	assert(str && sub);
	int strLen = strlen(str);
	int subLen = strlen(sub);
	if (subLen == 0)	return 0;//子串sub为空字符串
	if (strLen < subLen)	return -1;//主串长度小于子串长度
	if (pos < 0 || pos >= strLen)	return -1;//索引位置非法

	//nextval数组
	int* nextval = (int*)malloc(sizeof(int) * subLen);
	assert(nextval);//判断申请空间是否成功
	NextVal(sub, nextval, subLen);

	int i = pos;//遍历主串
	int j = 0;//遍历子串
	while (i < strLen && j < subLen)
	{
		if (j == -1 || str[i] == sub[j])
		{
			i++;
			j++;
		}
		else
		{
			j = nextval[j];
		}
	}
	if (j == subLen)//在主串中找到子串
	{
		free(nextval);
		nextval = NULL;
		return i - j;
	}
	else//在主串中找不到子串
	{
		free(nextval);
		nextval = NULL;
		return -1;
	}
}

int main()
{
	printf("%d\n", KMP2("ababcabcde", "abcd", 0));//5
	printf("%d\n", KMP2("ababcabcde", "abcdf", 0));//-1
	printf("%d\n", KMP2("ababcabcde", "ab", 0));//0
	printf("%d\n", KMP2("ababcabcde", "a", 0));//0
	printf("%d\n", KMP2("ababcabcde", "a", -1));//-1
	printf("%d\n", KMP2("ababcabcde", "a", 11));//-1
	printf("%d\n", KMP2("\0", "a", 0));//-1

	return 0;
}

找出字符串中第一个匹配项的下标

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例 1：

输入：haystack = "sadbutsad", needle = "sad"
输出：0
解释："sad" 在下标 0 和 6 处匹配。第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入：haystack = "leetcode", needle = "leeto"
输出：-1
解释："leeto" 没有在"leetcode" 中出现，所以返回 -1 。

void NextVal(char* needle, int* nextval, int len2)
{
    assert(needle);
    nextval[0] = -1;
    if(len2 == 1)
    {
        return;
    }   

    nextval[1] = 0;
    int i = 2;//当前i位置
    int k = 0;//前一项的k值
    //先将nextval数组初始化为next数组
    while(i < len2)
    {
        if(k == -1 || needle[i - 1] == needle[k])
        {
            nextval[i] = k + 1;
            i++;
            k++;
        }
        else
        {
            k = nextval[k];
        }
    }
	//修改nextval数组
	for (i = 2; i < len2; i++)
	{
		//回退到的位置上的字符和当前i位置上的字符相等
		//nextval[i]为回退到的位置
		//sub[nextval[i]]为回退到的位置上的字符
		if (needle[i] == needle[nextval[i]])
		{
			nextval[i] = nextval[nextval[i]];
		}
	}
}

int strStr(char * haystack, char * needle)
{
    assert(haystack && needle);
    int len1 = strlen(haystack);//haystack字符串的长度
    int len2 = strlen(needle);//needle字符串的长度
    if(len1 < len2) return -1;//主串长度小于子串长度
    
    //引入nextval数组
    int* nextval = (int*)malloc(sizeof(int) * len2);
    assert(nextval);//判断申请空间是否成功
    NextVal(needle, nextval, len2);

    int i = 0;//遍历主串
    int j = 0;//遍历子串
    while(i < len1 && j < len2)
    { 
        if(j == -1 || haystack[i] == needle[j])
        {
            i++;
            j++;
        }
        else
        {
        	//回溯
            j = nextval[j];
        }
    }
    if(j == len2)//在主串中找到子串   
    {
        free(nextval);
        nextval = NULL;
        return i - j;
    }
    else//在主串中找不到子串
    {
        free(nextval);
        nextval = NULL;
        return -1;
    }
}

总结

本篇博客主要讲解了库函数strstr的源码、模拟实现库函数strstr、BF算法以及KMP算法。博主相信这是全网最详细的字符串匹配算法讲解了，如果大家能够认真看完，肯定会有不少的收获。那就麻烦大家给个三连支持一下！谢谢大家啦！❣️