【数据结构初阶】Leetcode二叉树基础练习&&完全二叉树判断
大家好我是沐曦希
二叉树oj练习
- 1.单值二叉树
-
- 代码
- 2.相同的树
-
- 代码
- 3.二叉树的前序遍历
-
- 代码
- 4.二叉树的中序遍历
-
- 代码
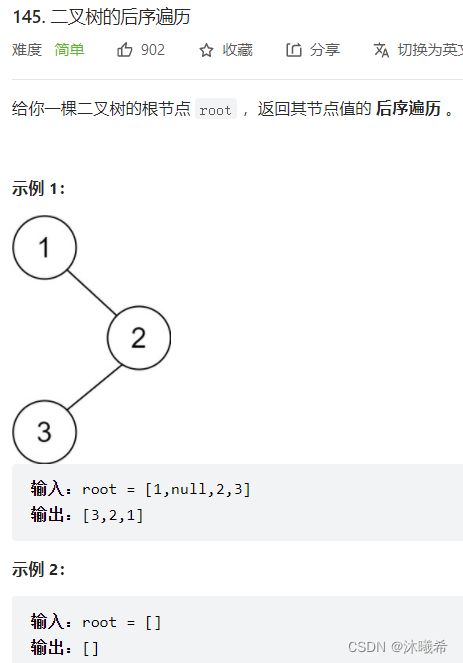
- 5.二叉树的后序遍历
-
- 代码
- 6.另一棵树的子树
-
- 代码
- 7.对称二叉树
-
- 代码
- 8.二叉树遍历
-
- 代码
- 9.层序遍历
-
- BinaryTree.h
- test.c
- BinaryTree.c
- 10.判断是否为完全二叉树
- 11.写在最后
1.单值二叉树
题目链接:965. 单值二叉树
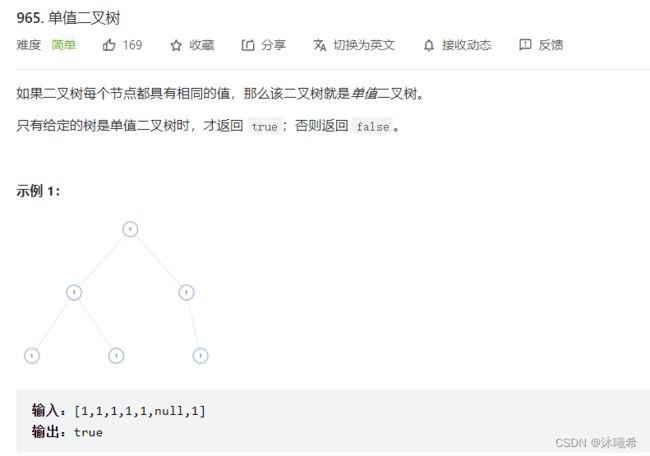
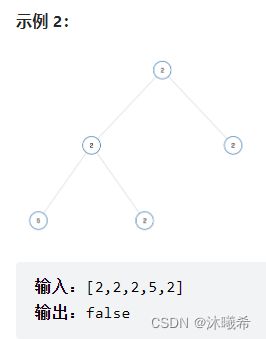
思路:
通过判断根与两子树比较,如果根与两个子树相等,那么就递归到下一个节点,不相等则返回false。即a==b,a==c,则b==c。
通过分治思想,把二叉树分为根与左右子树对比它们的值是否相等,相等则又把左子树和右子树分别看成它们子树的根继续对比,直到有不对或者对比完全。
代码
bool isUnivalTree(struct TreeNode* root){
if(root == NULL)
return true;
if(root->left && root->val != root->left->val )
return false;
if(root->right && root->val != root->right->val)
return false;
return isUnivalTree(root->left) && isUnivalTree(root->right);
}
2.相同的树
题目链接:100. 相同的树
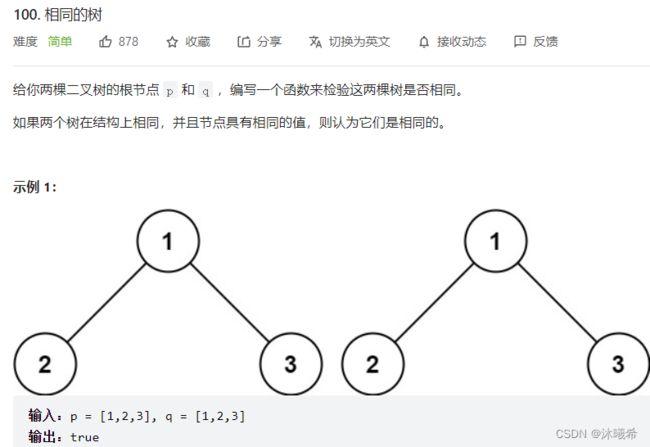
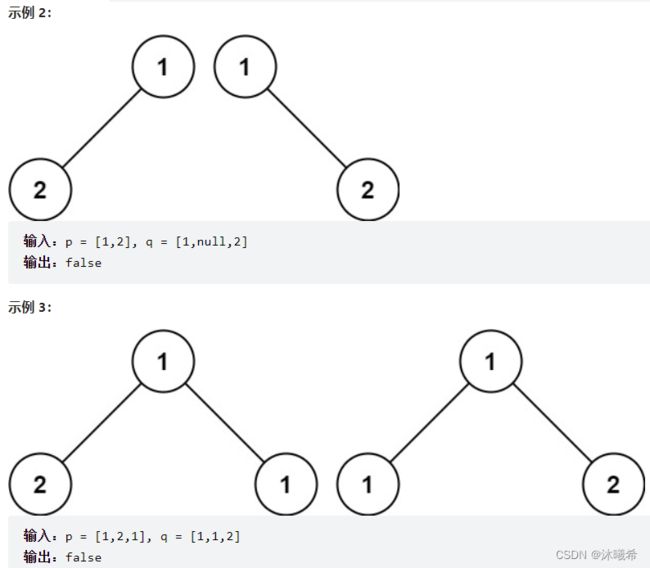
思路:
判断是否为相等的二棵树,那么首先要判断它们是否同时为空,同时为空则返回真;如果并同时为空则返回假。还剩下一种假情况:两科树根的值不相等,那么则返回空。
通过分治的思想继续将左子树和右子树分别看成其子树的根继续判断,以此类推。
代码
bool isSameTree(struct TreeNode* p, struct TreeNode* q){
if(p == NULL && q == NULL)
return true;
else if(q == NULL || p == NULL)
return false;
if(p->val != q->val)
return false;
return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
3.二叉树的前序遍历
题目链接:144. 二叉树的前序遍历
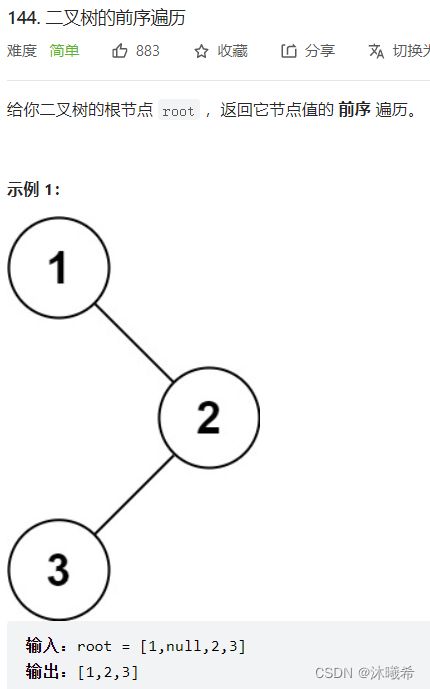
思路:
1.要将前序遍历的值存入数组中返回,那么需要动态开辟,因为栈帧会随着函数调用结束而销毁,而堆不会。为了便利开辟多少内存,可以实现一个递归函数来计算二叉树的节点个数。
2.因为要改变下标的值,那么就要传下标 i 的地址,否则会被后面的值覆盖。
3.因为是前序遍历储存,所以类似前序遍历一样,只是将打印改成了将数值储存进数组中。
此时需要注意的是:*因为后置++的优先级高于解引用,所以 pi 增加要加上括号,不加则越界访问了。
代码
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
return 0;
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void PreOrder(struct TreeNode* root, int* a, int* pi)
{
if(root == NULL)
return;
a[*pi] = root->val;
(*pi)++;
PreOrder(root->left,a,pi);
PreOrder(root->right,a,pi);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize){
int sz = TreeSize(root);
*returnSize = sz;
int* a = (int*) malloc(sizeof(int)*sz);
int i = 0;
PreOrder(root,a,&i);
return a;
}
4.二叉树的中序遍历
题目链接:94. 二叉树的中序遍历

和前序遍历很相似,都是把中序遍历中的打印改成储存。
代码
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
return 0;
return 1 + TreeSize(root->left)+TreeSize(root->right);
}
void InOrder(struct TreeNode* root, int* a, int* pi)
{
if(root==NULL)
{
return;
}
InOrder(root->left,a,pi);
a[*pi] = root->val;
(*pi)++;
InOrder(root->right,a,pi);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize){
int sz = TreeSize(root);
int* a = (int*)malloc(sizeof(int)*sz);
int i = 0;
InOrder(root,a,&i);
*returnSize = sz;
return a;
}
5.二叉树的后序遍历
代码
int TreeSize(struct TreeNode* root)
{
if(root == NULL)
return NULL;
return 1 + TreeSize(root->left) + TreeSize(root->right);
}
void PostOrder(struct TreeNode* root, int* a, int* pi)
{
if(root == NULL)
return;
PostOrder(root->left,a,pi);
PostOrder(root->right,a,pi);
a[*pi] = root->val;
(*pi)++;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize){
int sz = TreeSize(root);
int* a = (int*) malloc (sizeof(int)*sz);
int i = 0;
PostOrder(root,a,&i);
*returnSize = sz;
return a;
}
6.另一棵树的子树
题目链接:572. 另一棵树的子树


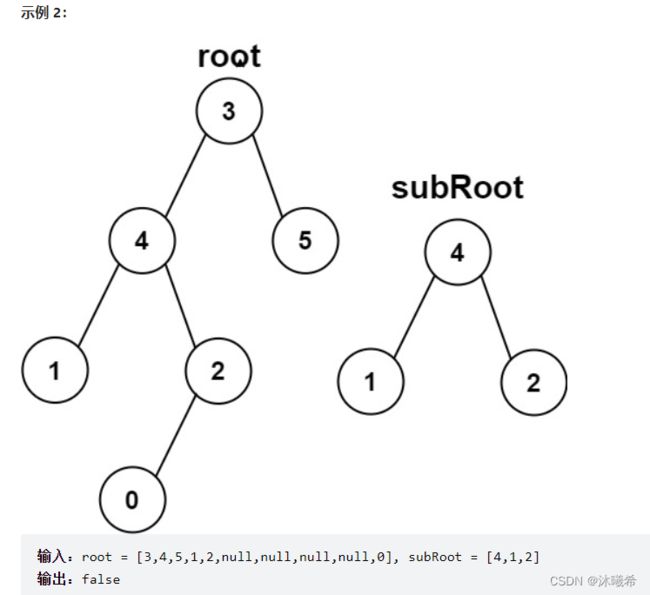
思路:
要在一个大树里面找到和小树一样的树,那么就像题目2.相同的树,只是要找到与小树根节点的值相同的节点,再调用题目二中的函数。
那么此时要在根,左子树和右子树中找,只要其中一个子树找到就为真,否则为假。
代码
bool isSameTree(struct TreeNode* root, struct TreeNode* subRoot)
{
if(root == NULL && subRoot == NULL)
return true;
else if(root == NULL || subRoot == NULL)
return false;
if(root->val != subRoot->val)
return false;
return isSameTree(root->left,subRoot->left) && isSameTree(root->right,subRoot->right);
}
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
if(root == NULL)
return false;
if(isSameTree(root,subRoot))
{
return true;
}
return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}
7.对称二叉树
题目链接:101. 对称二叉树

思路:
要判断是否为对称二叉树,对称二叉树即左子树和右子树关于根节点轴对称。
那么很类似相同的树,就可以通过更改判断相同的树的代码,传参中的两个参数应该传的是左子树的根节点,和右节点。
注意的是:因为是关于轴对称,那么就应该是判断左子树的左子树和右子树的右子树比对值是否相等,左子树的右子树和右子树的左子树是否相等,反过来。
isSameTree(left->left,right->right) && isSameTree(left->right,right->left);
代码
bool isSameTree(struct TreeNode* left, struct TreeNode* right)
{
if(left == NULL && right == NULL)
return true;
if(left == NULL|| right == NULL)
return false;
if(left->val != right->val)
return false;
return isSameTree(left->left,right->right) && isSameTree(left->right,right->left);
}
bool isSymmetric(struct TreeNode* root){
if(root == NULL)
return true;
return isSameTree(root->left , root->right);
}
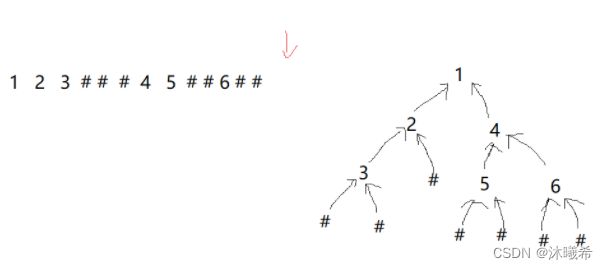
8.二叉树遍历
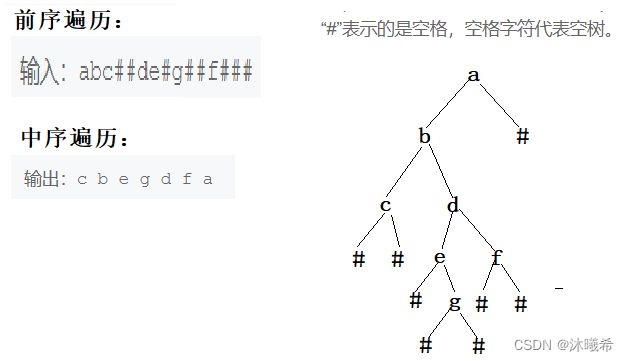
思路:
1.创建一个数组,传数组数组名和下标的地址 &i 给二叉树创建的函数。
2.首先要判断该元素是否为#,是则(*pi)++一下,返回NULL。
3.开辟一个二叉树节点,将该元素的的值赋值给新开辟的节点。(*pi)++一下。
4.因为输入结果是先序遍历(前序遍历),先序遍历是按照:根->左孩子->右孩子,那么先递归找到root->left,后递归找到root->right。
root->left = BinaryTreeCreate(a, pi);//递归创建左子树
root->right = BinaryTreeCreate(a, pi);//递归创建右子树
代码
#include9.层序遍历
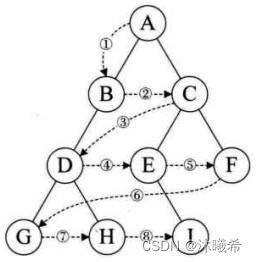
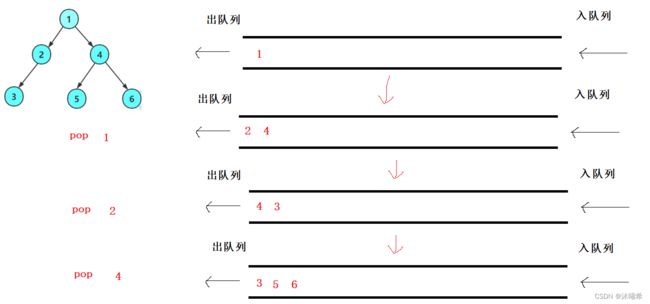
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
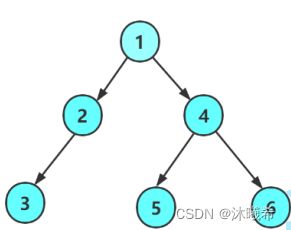
层序遍历可以通过数据结构的队列来实现。
1.初始化一个队列并且判断二叉树是否为空,不为空则入栈根节点。
2.取出队列中最左边节点并保存起来,pop掉该节点并打印该节点的值。如果该节点的左右孩子都不为空则入栈,依次类推。
3.当队列不为空则进行循环,如果为空则结束循环,此时就把二叉树层序遍历完全。
BinaryTree.h
#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#includetest.c
#include"BinaryTree.h"
void TreeLevelOrder(struct BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
printf("%d ", front->data);
// 下一层,入队列
if (front->left)
QueuePush(&q, front->left);
if (front->right)
QueuePush(&q, front->right);
}
printf("\n");
QueueDestroy(&q);
}
int main()
{
BTNode* root = CreateTree();
TreeLevelOrder(root);
BinaryTreeDestroy(root);
root = NULL;
return 0;
}
BinaryTree.c
#include"BinaryTree.h"
void QueueInit(Queue* qp)
{
qp->head = NULL;
qp->tail = NULL;
qp->size = 0;
}
void QueueDestroy(Queue* qp)
{
assert(qp);
QNode* cur = qp->head;
while (cur)
{
QNode* dele = cur;
cur = cur->next;
free(dele);
dele = NULL;
}
qp->head = NULL;
qp->tail = NULL;
qp->size = 0;
}
void QueuePush(Queue* qp, QDataType data)
{
assert(qp);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
printf("perror fail");
exit(-1);
}
else
{
newnode->val = data;
newnode->next = NULL;
}
if (qp->tail == NULL)
{
qp->head = newnode;
qp->tail = newnode;
}
else
{
qp->tail->next = newnode;
qp->tail = newnode;
}
++qp->size;
}
void QueuePop(Queue* qp)
{
assert(qp);
assert(!QueueEmpty(qp));
if (qp->head->next == NULL)
{
free(qp->head);
qp->head = NULL;
qp->tail = NULL;
qp->size = 0;
}
else
{
QNode* cur = qp->head;
qp->head = qp->head->next;
free(cur);
cur = NULL;
--qp->size;
}
}
bool QueueEmpty(Queue* qp)
{
assert(qp);
return qp->head == NULL && qp->tail == NULL;
}
QDataType QueueFront(Queue* qp)
{
assert(qp);
assert(!QueueEmpty(qp));
return qp->head->val;
}
QDataType QueueBack(Queue* qp)
{
assert(qp);
assert(!QueueEmpty(qp));
return qp->tail->val;
}
int QueueSize(Queue* qp)
{
assert(qp);
return qp->size;
}
void BinaryTreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
BinaryTreeDestroy(root->left);
BinaryTreeDestroy(root->right);
free(root);
}
BTNode* CreateTree()
{
BTNode* n1 = (BTNode*)malloc(sizeof(BTNode));
assert(n1);
BTNode* n2 = (BTNode*)malloc(sizeof(BTNode));
assert(n2);
BTNode* n3 = (BTNode*)malloc(sizeof(BTNode));
assert(n3);
BTNode* n4 = (BTNode*)malloc(sizeof(BTNode));
assert(n4);
BTNode* n5 = (BTNode*)malloc(sizeof(BTNode));
assert(n5);
BTNode* n6 = (BTNode*)malloc(sizeof(BTNode));
assert(n6);
BTNode* n7 = (BTNode*)malloc(sizeof(BTNode));
assert(n7);
n1->data = 1;
n2->data = 2;
n3->data = 3;
n4->data = 4;
n5->data = 5;
n6->data = 6;
n7->data = 7;
n1->left = n2;
n1->right = n4;
n2->left = n3;
n2->right = NULL;
n4->left = n5;
n4->right = n6;
n3->left = NULL;
n3->right = NULL;
n5->left = NULL;
n5->right = NULL;
n6->left = NULL;
n6->right = NULL;
return n1;
}
10.判断是否为完全二叉树
思路:
想要判断一个树是否为完全二叉树,那么要知道二叉树的概念:
1.二叉树的前h-1层都是满的,没有节点是空的。
2.最后一层至少有一个节点,最后一层必须连续,即左节点为空,那么右节点必须空,不能某一个节点不为空,前面节点为空。
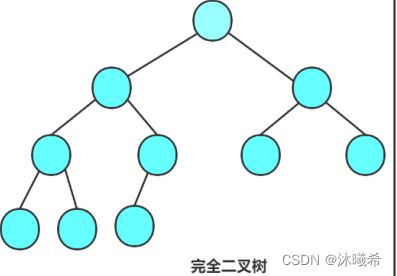
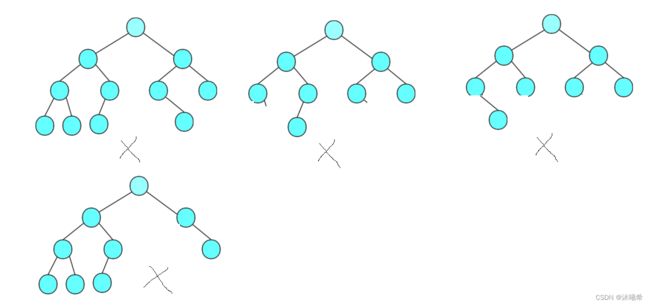
那么此时就需要通过层序遍历来解决这个问题。
一层一层的走,遇到空以后,后面不能为非空,有非空即为假。
和层序遍历很像。
bool BinaryTreeComplete(root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front == NULL)
break;
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
// 遇到空以后,后面全是空,则是完全二叉树
// 遇到空以后,后面存在非空,则不是完全二叉树
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
}
QueueDestroy(&q);
return true;
}