LeetCode刷题Python实录
使用Python的LeetCode刷题
- 前言
- 题目
-
- 1408. 数组中的字符串匹配
- 508. 出现次数最多的子树元素和
- 1089. 复写零
- 剑指 Offer 14- I. 剪绳子
- 1175. 质数排列
- 1108. IP 地址无效化
- 648. 单词替换
- 513. 找树左下角的值
- 30. 串联所有单词的子串
- 814. 二叉树剪枝
- 871. 最低加油次数
- 873. 最长的斐波那契子序列的长度
- 515. 在每个树行中找最大值
- 535. TinyURL 的加密与解密
- 324. 摆动排序 II
- 241. 为运算表达式设计优先级
- 522. 最长特殊序列 II
- 剑指 Offer II 091. 粉刷房子
- 729. 我的日程安排表 I
- 710. 黑名单中的随机数
- 1252. 奇数值单元格的数目
- 1260. 二维网格迁移
- 757. 设置交集大小至少为2
- END
前言
博主使用Python在leetcode刷题的实录代码与视频
佛系更新中~
视频链接:https://space.bilibili.com/1102086181
题目
1408. 数组中的字符串匹配
题目
给你一个字符串数组 words ,数组中的每个字符串都可以看作是一个单词。请你按 任意 顺序返回 words 中是其他单词的子字符串的所有单词。
如果你可以删除 words[j] 最左侧和/或最右侧的若干字符得到 word[i] ,那么字符串 words[i] 就是 words[j] 的一个子字符串。
示例 1:
输入:words = [“mass”,“as”,“hero”,“superhero”]
输出:[“as”,“hero”]
解释:“as” 是 “mass” 的子字符串,“hero” 是 “superhero” 的子字符串。
[“hero”,“as”] 也是有效的答案。
示例 2:
输入:words = [“leetcode”,“et”,“code”]
输出:[“et”,“code”]
解释:“et” 和 “code” 都是 “leetcode” 的子字符串。
示例 3:
输入:words = [“blue”,“green”,“bu”]
输出:[]
提示:
1 <= words.length <= 100
1 <= words[i].length <= 30
words[i] 仅包含小写英文字母。
题目数据 保证 每个 words[i] 都是独一无二的。
代码
class Solution:
def stringMatching(self, words: List[str]) -> List[str]:
ans = []
for i, x in enumerate(words):
for j, y in enumerate(words):
if i != j and x in y:
ans.append(x)
break
return ans
508. 出现次数最多的子树元素和
给你一个二叉树的根结点 root ,请返回出现次数最多的子树元素和。如果有多个元素出现的次数相同,返回所有出现次数最多的子树元素和(不限顺序)。
一个结点的 「子树元素和」 定义为以该结点为根的二叉树上所有结点的元素之和(包括结点本身)。
示例 1:
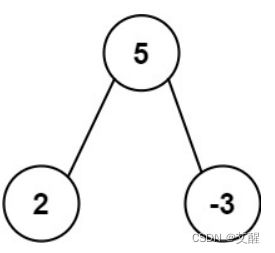
输入: root = [5,2,-3]
输出: [2,-3,4]
示例 2:
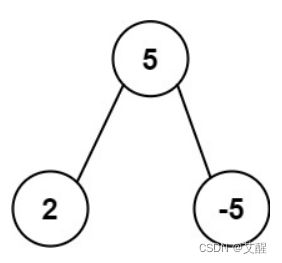
输入: root = [5,2,-5]
输出: [2]
提示:
节点数在 [1, 104] 范围内
-105 <= Node.val <= 105
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findFrequentTreeSum(self, root: TreeNode) -> List[int]:
node_dict = dict()
def node_sum(root:TreeNode):
if root is None:
return 0
data = root.val + node_sum(root.left) + node_sum(root.right)
if data not in node_dict.keys():
node_dict[data] = 1
else:
node_dict[data] += 1
return data
node_sum(root)
node_dict = sorted(node_dict.items(), key=lambda x:x[1], reverse=True)
sum_list = list()
max_sum = node_dict[0][1]
for item in node_dict:
if item[1] == max_sum:
sum_list.append(item[0])
return sum_list
1089. 复写零
给你一个长度固定的整数数组 arr,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。
注意:请不要在超过该数组长度的位置写入元素。
要求:请对输入的数组 就地 进行上述修改,不要从函数返回任何东西。
示例 1:
输入:[1,0,2,3,0,4,5,0]
输出:null
解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]
示例 2:
输入:[1,2,3]
输出:null
解释:调用函数后,输入的数组将被修改为:[1,2,3]
提示:
1 <= arr.length <= 10000
0 <= arr[i] <= 9
class Solution:
def duplicateZeros(self, arr: List[int]) -> None:
"""
Do not return anything, modify arr in-place instead.
"""
length = len(arr)
for i in range(length):
if arr[i] == 0:
arr.append(0)
i = length - 1
j = len(arr) - 1
while i >= 0:
if arr[i] == 0:
arr[j] = 0
j-=1
i-=1
arr[j]=0
j-=1
else:
arr[j] = arr[i]
j-=1
i-=1
for i in range(len(arr) - length):
arr.pop()
剑指 Offer 14- I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
class Solution:
def cuttingRope(self, n: int) -> int:
dp = [0] * 60
for i in range(2, n+1):
for j in range(1, i):
dp[i] = max(dp[i], j * max(dp[i-j], i-j))
return dp[n]
1175. 质数排列
题目
请你帮忙给从 1 到 n 的数设计排列方案,使得所有的「质数」都应该被放在「质数索引」(索引从 1 开始)上;你需要返回可能的方案总数。
让我们一起来回顾一下「质数」:质数一定是大于 1 的,并且不能用两个小于它的正整数的乘积来表示。
由于答案可能会很大,所以请你返回答案 模 mod 10^9 + 7 之后的结果即可。
示例 1:
输入:n = 5
输出:12
解释:举个例子,[1,2,5,4,3] 是一个有效的排列,但 [5,2,3,4,1] 不是,因为在第二种情况里质数 5 被错误地放在索引为 1 的位置上。
示例 2:
输入:n = 100
输出:682289015
提示:
1 <= n <= 100
视频
LeetCode刷题实录——简单的求质数问题,1175. 质数排列
代码
class Solution:
def numPrimeArrangements(self, n: int) -> int:
# 质数的个数和质数索引数相同,这里用到了排列组合
# 质数个数的阶乘*不是质数个数的阶乘 % mod就是答案
mod = 10 ** 9 + 7
# 接下来一边线性筛,一边统计质数个数
cnt = 0
prm = [0 for i in range(n + 1)]
for i in range(2, n+1):
if prm[i] == 0:
cnt += 1
j = 2
while j * i <= n:
prm[j * i] = 1
j += 1
ans = 1
for i in range(1, cnt+1):
ans *= i
ans %= mod
for i in range(1, n - cnt+1):
ans *= i
ans %= mod
return ans
1108. IP 地址无效化
题目
给你一个有效的 IPv4 地址 address,返回这个 IP 地址的无效化版本。
所谓无效化 IP 地址,其实就是用 “[.]” 代替了每个 “.”。
示例 1:
输入:address = “1.1.1.1”
输出:“1[.]1[.]1[.]1”
示例 2:
输入:address = “255.100.50.0”
输出:“255[.]100[.]50[.]0”
提示:
给出的 address 是一个有效的 IPv4 地址
视频
Python字符串不支持修改,那就不怪我偷懒了——LeetCode刷题实录 1108. IP 地址无效化
代码
class Solution:
def defangIPaddr(self, address: str) -> str:
# 既然python不支持字符串字符的替换,那么就来点python特性的解法
ip = address.split('.')
return ip[0] + "[.]" + ip[1] + "[.]" + ip[2] + "[.]" + ip[3]
648. 单词替换
题目
在英语中,我们有一个叫做 词根(root) 的概念,可以词根后面添加其他一些词组成另一个较长的单词——我们称这个词为 继承词(successor)。例如,词根an,跟随着单词 other(其他),可以形成新的单词 another(另一个)。
现在,给定一个由许多词根组成的词典 dictionary 和一个用空格分隔单词形成的句子 sentence。你需要将句子中的所有继承词用词根替换掉。如果继承词有许多可以形成它的词根,则用最短的词根替换它。
你需要输出替换之后的句子。
示例 1:
输入:dictionary = [“cat”,“bat”,“rat”], sentence = “the cattle was rattled by the battery”
输出:“the cat was rat by the bat”
示例 2:
输入:dictionary = [“a”,“b”,“c”], sentence = “aadsfasf absbs bbab cadsfafs”
输出:“a a b c”
提示:
1 <= dictionary.length <= 1000
1 <= dictionary[i].length <= 100
dictionary[i] 仅由小写字母组成。
1 <= sentence.length <= 10^6
sentence 仅由小写字母和空格组成。
sentence 中单词的总量在范围 [1, 1000] 内。
sentence 中每个单词的长度在范围 [1, 1000] 内。
sentence 中单词之间由一个空格隔开。
sentence 没有前导或尾随空格。
视频
LeetCode刷题实录——python, 648. 单词替换
代码
class Solution:
def replaceWords(self, dictionary: List[str], sentence: str) -> str:
st = set(dictionary) #建立集合来表明有多少词根,注意词根只是开头,后面遍历会用到
sents = sentence.split(" ")
for i in range(len(sents)): # 挨个取单词
for j in range(len(sents[i])): # 从前向后取词根,即前缀
if sents[i][:j] in st:
# 嘶~这里好像字典解决不了,逆向思维一下,我们不把字典的值赋给他就好了
sents[i] = sents[i][:j] # 这样一定可以解决
return " ".join(sents)
513. 找树左下角的值
题目
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
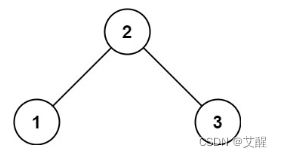
输入: root = [2,1,3]
输出: 1
示例 2:
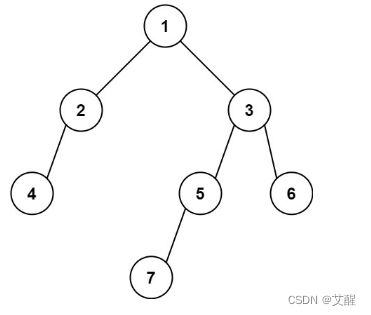
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
提示:
二叉树的节点个数的范围是 [1,104]
-231 <= Node.val <= 231 - 1
视频
LeetCode刷题实录——深度优先搜索实现 513. 找树左下角的值
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
def getLevel(root:Optional[TreeNode], level):
cur_val, cur_level = root.val, level
if root.left is not None:
cur_val, cur_level = getLevel(root.left, level+1)
if root.right is not None:
r_val, r_level = getLevel(root.right, level+1)
if r_level > cur_level:
cur_val, cur_level = r_val, r_level
return cur_val, cur_level
cur_val, cur_level = root.val, 0
if root.left is not None:
cur_val, cur_level = getLevel(root.left, 1)
if root.right is not None:
r_val, r_level = getLevel(root.right, 1)
if r_level > cur_level:
cur_val, cur_level = r_val, r_level
return cur_val
30. 串联所有单词的子串
题目
给定一个字符串 s 和一些 长度相同 的单词 words 。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
注意子串要与 words 中的单词完全匹配,中间不能有其他字符 ,但不需要考虑 words 中单词串联的顺序。
示例 1:
输入:s = “barfoothefoobarman”, words = [“foo”,“bar”]
输出:[0,9]
解释:
从索引 0 和 9 开始的子串分别是 “barfoo” 和 “foobar” 。
输出的顺序不重要, [9,0] 也是有效答案。
示例 2:
输入:s = “wordgoodgoodgoodbestword”, words = [“word”,“good”,“best”,“word”]
输出:[]
示例 3:
输入:s = “barfoofoobarthefoobarman”, words = [“bar”,“foo”,“the”]
输出:[6,9,12]
提示:
1 <= s.length <= 104
s 由小写英文字母组成
1 <= words.length <= 5000
1 <= words[i].length <= 30
words[i] 由小写英文字母组成
视频
Leetcode刷题实录——python滑动窗口 30. 串联所有单词的子串
代码
from collections import Counter
class Solution:
def findSubstring(self, s: str, words: List[str]) -> List[int]:
s_len = len(s)
w_len = len(words[0])
ws_len = len(words)
ans = []
for i in range(s_len):
if i + w_len * ws_len <= s_len:
cnt = Counter()
for j in range(i, i + w_len * ws_len, w_len):
if s[j:j+w_len] in words:
cnt[s[j:j+w_len]] += 1
for word in words:
cnt[word] -= 1
if cnt[word] == 0:
del cnt[word]
if len(cnt) == 0:
ans.append(i)
return ans
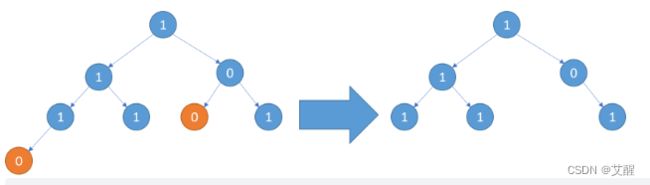
814. 二叉树剪枝
题目
给你二叉树的根结点 root ,此外树的每个结点的值要么是 0 ,要么是 1 。
返回移除了所有不包含 1 的子树的原二叉树。
节点 node 的子树为 node 本身加上所有 node 的后代。
输入:root = [1,null,0,0,1]
输出:[1,null,0,null,1]
解释:
只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。
示例 2:
输入:root = [1,0,1,0,0,0,1]
输出:[1,null,1,null,1]
示例 3:
输入:root = [1,1,0,1,1,0,1,0]
输出:[1,1,0,1,1,null,1]
提示:
树中节点的数目在范围 [1, 200] 内
Node.val 为 0 或 1
视频
LeetCode刷题实录——Python, 814. 二叉树剪枝,深度优先搜索,递归
代码
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pruneTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 深度优先搜索,如果左右子树均可删除或者当前结点为叶子结点则去除
def cut(root)->bool:
if root.left is not None:
left = cut(root.left)
if left:
root.left = None
if root.right is not None:
right = cut(root.right)
if right:
root.right = None
if root.val == 0 and root.left is None and root.right is None:
# 叶子结点为0说明这个结点应该删除
return True
return False
head = cut(root)
if head:
return None
else:
return root
871. 最低加油次数
题目
汽车从起点出发驶向目的地,该目的地位于出发位置东面 target 英里处。
沿途有加油站,每个 station[i] 代表一个加油站,它位于出发位置东面 station[i][0] 英里处,并且有 station[i][1] 升汽油。
假设汽车油箱的容量是无限的,其中最初有 startFuel 升燃料。它每行驶 1 英里就会用掉 1 升汽油。
当汽车到达加油站时,它可能停下来加油,将所有汽油从加油站转移到汽车中。
为了到达目的地,汽车所必要的最低加油次数是多少?如果无法到达目的地,则返回 -1 。
注意:如果汽车到达加油站时剩余燃料为 0,它仍然可以在那里加油。如果汽车到达目的地时剩余燃料为 0,仍然认为它已经到达目的地。
示例 1:
输入:target = 1, startFuel = 1, stations = []
输出:0
解释:我们可以在不加油的情况下到达目的地。
示例 2:
输入:target = 100, startFuel = 1, stations = [[10,100]]
输出:-1
解释:我们无法抵达目的地,甚至无法到达第一个加油站。
示例 3:
输入:target = 100, startFuel = 10, stations = [[10,60],[20,30],[30,30],[60,40]]
输出:2
解释:
我们出发时有 10 升燃料。
我们开车来到距起点 10 英里处的加油站,消耗 10 升燃料。将汽油从 0 升加到 60 升。
然后,我们从 10 英里处的加油站开到 60 英里处的加油站(消耗 50 升燃料),
并将汽油从 10 升加到 50 升。然后我们开车抵达目的地。
我们沿途在1两个加油站停靠,所以返回 2 。
提示:
1 <= target, startFuel, stations[i][1] <= 10^9
0 <= stations.length <= 500
0 < stations[0][0] < stations[1][0] < … < stations[stations.length-1][0] < target
视频
LeetCode刷实录——Python贪心算法,871. 最低加油次数
代码
class Solution:
def minRefuelStops(self, target: int, startFuel: int, stations: List[List[int]]) -> int:
'''
第一时间想到的是递归, 但是递归会超时,大概能过100多个测试点
仔细思考一下,假设我们是四维生物,我们可以穿越时间,在油用完的时候可以查看之前经过加油站
什么时候加油,什么时候不加油
用这种思路的贪心算法
'''
ans = 0
h = [] # 这里维护一个大顶堆,在非leetcode的环境需要 from heapq import heappop, heappush
cur = 0
curFuel = startFuel
for stat in stations:
dist, fuel = stat[0], stat[1]
curFuel -= dist - cur
cur = dist
# 只有没油,并且前面有加油站的时候我们才会考虑要是在哪里加油就有油了
while curFuel < 0 and h:
ans += 1
curFuel -= heappop(h) # 因为这个函数是维护小顶堆的,所以我们取负
if curFuel < 0: # 全部加上都不够自然达不到
return -1
heappush(h, -fuel) # 能到这个停车场(dist位置),那么可以选择加或者不加了
# 注意最后还要看cur与target的位置关系
curFuel -= target - cur
cur = target # 其实这句可以省去
while curFuel < 0 and h:
ans += 1
curFuel -= heappop(h) # 因为这个函数是维护小顶堆的,所以我们取负
if curFuel < 0: # 全部加上都不够自然达不到
return -1
return ans
873. 最长的斐波那契子序列的长度
如果序列 X_1, X_2, …, X_n 满足下列条件,就说它是 斐波那契式 的:
n >= 3
对于所有 i + 2 <= n,都有 X_i + X_{i+1} = X_{i+2}
给定一个严格递增的正整数数组形成序列 arr ,找到 arr 中最长的斐波那契式的子序列的长度。如果一个不存在,返回 0 。
(回想一下,子序列是从原序列 arr 中派生出来的,它从 arr 中删掉任意数量的元素(也可以不删),而不改变其余元素的顺序。例如, [3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的一个子序列)
示例 1:
输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。
示例 2:
输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18] 。
提示:
3 <= arr.length <= 1000
1 <= arr[i] < arr[i + 1] <= 10^9
视频
LeetCode刷题实录——Python动态规划,873. 最长的斐波那契子序列的长度
代码
class Solution:
def lenLongestFibSubseq(self, arr: List[int]) -> int:
# 动态规划
# 我们假设dp[i][j]是arr第i个位置的数与第j个位置的数可以组成子序列
# 为了方便表示我们将arr转化成一个位置与数值对应的字典
idx = {x:i for i, x in enumerate(arr)} # {数值:索引},用于后边由数值直接找到数值位置
# 注意一下1 <= arr[i] < arr[i + 1] <= 10^9 并且严格递增的正整数数组
# 后面的一些操作和这两个特性有关
cnt = 0 # 计数器
n = len(arr)
dp = [[0] * n for _ in range(n)]
# dp是按照索引位dp的
for i, x in enumerate(arr):
if i != 0: # i是第一个的时候前面不会有数
for j in range(i-1, -1, -1):
# i从前向后,j从后向前,我们这里需要的是dp[j][i],并且j
# if arr[j] * 2 <= x:
# # 这时已经找不到在j之前的k了,如果能找到也一定是位于他们后边的了
# break
# 如果不这样修改还有其他修改方式
if x - arr[j] in idx: # 因为严格单调增,所以x-arr[j]一定>0
k = idx[x - arr[j]]
# 如果x - arr[j] 在字典里,说明k位置上的数与j,i位置上的数构成子序列
if k < j: # 这种修改可能更容易理解一点
dp[j][i] = max(dp[k][j]+1, 3)
#dp[j][i] 为k,j能组成的子序列数+1与3之间的最大值(一定存在k,j,i这三个)
cnt = max(cnt, dp[j][i])
return cnt
515. 在每个树行中找最大值
题目
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:
输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
示例2:
输入: root = [1,2,3]
输出: [1,3]
提示:
二叉树的节点个数的范围是 [0,104]
-231 <= Node.val <= 231 - 1
视频
LeetCode刷题实录——Python广度优先搜索,515. 在每个树行中找最大值
代码
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
import queue
class Solution:
def largestValues(self, root: Optional[TreeNode]) -> List[int]:
q = queue.Queue()
ans = []
if root is None:
return ans
q.put([root, 0])
curidx = -1
while not q.empty():
node, idx = q.get()
if idx > curidx:
ans.append(node.val)
curidx = idx
elif idx == curidx and ans[idx] < node.val:
ans[idx] = node.val
if node.left is not None:
q.put([node.left, idx+1])
if node.right is not None:
q.put([node.right, idx+1])
return ans
535. TinyURL 的加密与解密
题目
TinyURL 是一种 URL 简化服务, 比如:当你输入一个 URL https://leetcode.com/problems/design-tinyurl 时,它将返回一个简化的URL http://tinyurl.com/4e9iAk 。请你设计一个类来加密与解密 TinyURL 。
加密和解密算法如何设计和运作是没有限制的,你只需要保证一个 URL 可以被加密成一个 TinyURL ,并且这个 TinyURL 可以用解密方法恢复成原本的 URL 。
实现 Solution 类:
Solution() 初始化 TinyURL 系统对象。
String encode(String longUrl) 返回 longUrl 对应的 TinyURL 。
String decode(String shortUrl) 返回 shortUrl 原本的 URL 。题目数据保证给定的 shortUrl 是由同一个系统对象加密的。
示例:
输入:url = “https://leetcode.com/problems/design-tinyurl”
输出:“https://leetcode.com/problems/design-tinyurl”
解释:
Solution obj = new Solution();
string tiny = obj.encode(url); // 返回加密后得到的 TinyURL 。
string ans = obj.decode(tiny); // 返回解密后得到的原本的 URL 。
提示:
1 <= url.length <= 104
题目数据保证 url 是一个有效的 URL
视频
535. TinyURL 的加密与解密——嘶~一道简单题,刚开始想的麻烦了(LeetCode刷题Python实录)
代码
class Codec:
def __init__(self):
self.Dict = dict()
self.V2K = dict()
self.cur = 0
def encode(self, longUrl: str) -> str:
"""Encodes a URL to a shortened URL.
"""
idx = len(longUrl) - 1
st1 = ""
while idx >= 0 and longUrl[idx] != '/':
st1 = longUrl[idx] + st1
idx -= 1
if st1 in self.V2K.keys():
return longUrl[:idx+1] + self.V2K.get(st1)
else:
self.cur += 1
self.Dict[str(self.cur)] = st1
self.V2K[st1] = str(self.cur)
return longUrl[:idx+1] + self.V2K.get(st1)
def decode(self, shortUrl: str) -> str:
"""Decodes a shortened URL to its original URL.
"""
idx = len(shortUrl) - 1
st1 = ""
while idx >= 0 and shortUrl[idx] != '/':
st1 = shortUrl[idx] + st1
idx -= 1
return shortUrl[:idx+1] + self.Dict[st1]
# Your Codec object will be instantiated and called as such:
# codec = Codec()
# codec.decode(codec.encode(url))
324. 摆动排序 II
题目
给你一个整数数组 nums,将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。
你可以假设所有输入数组都可以得到满足题目要求的结果。
示例 1:
输入:nums = [1,5,1,1,6,4]
输出:[1,6,1,5,1,4]
解释:[1,4,1,5,1,6] 同样是符合题目要求的结果,可以被判题程序接受。
示例 2:
输入:nums = [1,3,2,2,3,1]
输出:[2,3,1,3,1,2]
提示:
1 <= nums.length <= 5 * 104
0 <= nums[i] <= 5000
题目数据保证,对于给定的输入 nums ,总能产生满足题目要求的结果
视频
324. 摆动排序 II——算是一个思维题吧(LeetCode刷题Python实录)
代码
class Solution:
def wiggleSort(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
arr = sorted(nums)
# 排序后截取后一半作为大于的数,前一半作为小于的数
length = len(nums)
length1 = (length + 1) // 2
j = length1 - 1 # 从小于的数里取
k = length - 1 # 从大于的数里取
for i in range(0, length, 2):
# 先取小的
nums[i] = arr[j] # 这是从后取,其实前后取无所谓的
if i + 1 < length:
nums[i+1] = arr[k]
j -= 1
k -= 1
241. 为运算表达式设计优先级
题目
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 104 。
示例 1:
输入:expression = “2-1-1”
输出:[0,2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2
示例 2:
输入:expression = “23-45”
输出:[-34,-14,-10,-10,10]
解释:
(2*(3-(45))) = -34
((23)-(45)) = -14
((2(3-4))5) = -10
(2((3-4)5)) = -10
(((23)-4)*5) = 10
提示:
1 <= expression.length <= 20
expression 由数字和算符 ‘+’、‘-’ 和 ‘*’ 组成。
输入表达式中的所有整数值在范围 [0, 99]
视频
LeetCode刷题实录——Python分治算法,241. 为运算表达式设计优先级
代码
class Solution:
def diffWaysToCompute(self, expression: str) -> List[int]:
'''
像这种题目优先考虑分治法
那么问题就变成了怎么个分法
很明显,我们可以选取优先级最低的去遍历,这样优先级左边和右边的计算可视为已经算完了(递归)
然后再计算这个最低优先级
计算左边和右边的同理
因为规模减少了,所以一定能出结果
'''
if expression.isdigit(): # 边界条件,isdigit用于判断是否纯数字,刚才错误的方式忽略了多位数字的影响
return [int(expression)]
ans = [] # 作为结果返回的列表
for i, st in enumerate(expression):
if st in ["-", "+", "*"]: # 只按照符号进行遍历,因为一旦符号的顺序确定了,数字顺序一定确定
left = self.diffWaysToCompute(expression[:i]) # 左侧得出的所有可能性
right = self.diffWaysToCompute(expression[i+1:]) # 右侧得出的所有可能性
'''
接下来很关键
我们已经知道了左侧和右侧所有的可能性了
要知道总体的可能性
我们需要逐一运算,怎么个运算法,取决于st
'''
for l in left:
for r in right:
if st == "-":
ans.append(l - r)
elif st == "+":
ans.append(l + r)
elif st == "*":
ans.append(l * r)
return ans
522. 最长特殊序列 II
题目
给定字符串列表 strs ,返回其中 最长的特殊序列 的长度。如果最长特殊序列不存在,返回 -1 。
特殊序列 定义如下:该序列为某字符串 独有的子序列(即不能是其他字符串的子序列)。
s 的 子序列可以通过删去字符串 s 中的某些字符实现。
例如,“abc” 是 “aebdc” 的子序列,因为您可以删除"aebdc"中的下划线字符来得到 “abc” 。“aebdc"的子序列还包括"aebdc”、 “aeb” 和 “” (空字符串)。
示例 1:
输入: strs = [“aba”,“cdc”,“eae”]
输出: 3
示例 2:
输入: strs = [“aaa”,“aaa”,“aa”]
输出: -1
提示:
2 <= strs.length <= 50
1 <= strs[i].length <= 10
strs[i] 只包含小写英文字母
视频
LeetCode刷题实录——暴力破解,简简单单,522. 最长特殊序列 II
代码
class Solution:
def findLUSlength(self, strs: List[str]) -> int:
# 数据量很小,可以直接暴力
length = len(strs)
max_len = -1
def check(s1:str, s2:str) ->bool:
i = 0
j = 0
l1 = len(s1)
l2 = len(s2)
while i < l1 and j < l2:
if s1[i] == s2[j]:
i += 1
j += 1
else:
j += 1
return j==l2 and i != l1 # 如果返回值为真,说明s2匹配到末尾都没有完全匹配上s1
for i in range(length):
flag = True
for j in range(length):
if i != j:
flag &= check(strs[i], strs[j]) # 这个函数现在写
if flag:
max_len = max(max_len, len(strs[i]))
return max_len
剑指 Offer II 091. 粉刷房子
题目
假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。
例如,costs[0][0] 表示第 0 号房子粉刷成红色的成本花费;costs[1][2] 表示第 1 号房子粉刷成绿色的花费,以此类推。
请计算出粉刷完所有房子最少的花费成本。
示例 1:
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色,1 号房子粉刷成绿色,2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。
示例 2:
输入: costs = [[7,6,2]]
输出: 2
提示:
costs.length == n
costs[i].length == 3
1 <= n <= 100
1 <= costs[i][j] <= 20
视频
LeetCode刷题实录——Python动态规划及其优化,剑指 Offer II 091. 粉刷房子
代码
class Solution:
def minCost(self, costs: List[List[int]]) -> int:
length = len(costs)
dp = [[0, 0, 0] for _ in range(length)]
dp[0] = costs[0]
for i in range(1, length):
for j in range(3):
dp[i][j] = min(dp[i-1][(j+1)%3], dp[i-1][(j+2)%3]) + costs[i][j]
return min(dp[length-1])
class Solution:
def minCost(self, costs: List[List[int]]) -> int:
# 下面来讲一下优化
# 由于状态转移是由i-1向i转移的,所以我们就不需要i了,直接利用循环转移即可
length = len(costs)
# dp = [[0, 0, 0] for _ in range(length)]
dp = costs[0].copy()
for i in range(1, length):
dp = [min(dp[(j+1)%3], dp[(j+2)%3]) + c for j, c in enumerate(costs[i])]
return min(dp)
729. 我的日程安排表 I
题目
实现一个 MyCalendar 类来存放你的日程安排。如果要添加的日程安排不会造成 重复预订 ,则可以存储这个新的日程安排。
当两个日程安排有一些时间上的交叉时(例如两个日程安排都在同一时间内),就会产生 重复预订 。
日程可以用一对整数 start 和 end 表示,这里的时间是半开区间,即 [start, end), 实数 x 的范围为, start <= x < end 。
实现 MyCalendar 类:
MyCalendar() 初始化日历对象。
boolean book(int start, int end) 如果可以将日程安排成功添加到日历中而不会导致重复预订,返回 true 。否则,返回 false 并且不要将该日程安排添加到日历中。
示例:
输入:
[“MyCalendar”, “book”, “book”, “book”]
[[], [10, 20], [15, 25], [20, 30]]
输出:
[null, true, false, true]
解释:
MyCalendar myCalendar = new MyCalendar();
myCalendar.book(10, 20); // return True
myCalendar.book(15, 25); // return False ,这个日程安排不能添加到日历中,因为时间 15 已经被另一个日程安排预订了。
myCalendar.book(20, 30); // return True ,这个日程安排可以添加到日历中,因为第一个日程安排预订的每个时间都小于 20 ,且不包含时间 20 。
提示:
0 <= start < end <= 109
每个测试用例,调用 book 方法的次数最多不超过 1000 次。
视频
LeetCode刷题实录——Python二分,729. 我的日程安排表 I
代码
from sortedcontainers import SortedDict
class MyCalendar:
'''
由题意可得,如果我们按照时间顺序存储日程安排,那么就省去了排序这一过程,并且查询可以使用二分
这里使用SortedDict来维护一个有顺序的日程安排
'''
def __init__(self):
self.books = SortedDict()
def book(self, start: int, end: int) -> bool:
# 这里我们按照end进行左查找,也可以按照start进行右查找,不过边界条件的判断会稍微的麻烦些
idx = self.books.bisect_left(end) # 查找到字典键值所在位置或者键值应该插入的位置
if idx == 0 or self.books.items()[idx-1][1] <= start:
# 这里做下解释,第一种情况如果idx == 0,说明end小于时间顺序中任何一个键值,直接插入
# 第二种情况,因为查找的是键值所在位置,那么end后面的时间安排开始时间一定是 >= end的
# 所以只用考虑start的值和前一个日程安排的位置的结束时间,如果结束时间 <= start说明满足条件
# 入字典,返回True
self.books[start] = end
return True
return False
# Your MyCalendar object will be instantiated and called as such:
# obj = MyCalendar()
# param_1 = obj.book(start,end)
710. 黑名单中的随机数
题目
给定一个整数 n 和一个 无重复 黑名单整数数组 blacklist 。设计一种算法,从 [0, n - 1] 范围内的任意整数中选取一个 未加入 黑名单 blacklist 的整数。任何在上述范围内且不在黑名单 blacklist 中的整数都应该有 同等的可能性 被返回。
优化你的算法,使它最小化调用语言 内置 随机函数的次数。
实现 Solution 类:
Solution(int n, int[] blacklist) 初始化整数 n 和被加入黑名单 blacklist 的整数
int pick() 返回一个范围为 [0, n - 1] 且不在黑名单 blacklist 中的随机整数
示例 1:
输入
[“Solution”, “pick”, “pick”, “pick”, “pick”, “pick”, “pick”, “pick”]
[[7, [2, 3, 5]], [], [], [], [], [], [], []]
输出
[null, 0, 4, 1, 6, 1, 0, 4]
解释
Solution solution = new Solution(7, [2, 3, 5]);
solution.pick(); // 返回0,任何[0,1,4,6]的整数都可以。注意,对于每一个pick的调用,
// 0、1、4和6的返回概率必须相等(即概率为1/4)。
solution.pick(); // 返回 4
solution.pick(); // 返回 1
solution.pick(); // 返回 6
solution.pick(); // 返回 1
solution.pick(); // 返回 0
solution.pick(); // 返回 4
提示:
1 <= n <= 109
0 <= blacklist.length <= min(105, n - 1)
0 <= blacklist[i] < n
blacklist 中所有值都 不同
pick 最多被调用 2 * 104 次
视频
LeetCode刷题实录——今天的题目有点难,710. 黑名单中的随机数
代码
class Solution:
def __init__(self, n: int, blacklist: List[int]):
self.bound = n - len(blacklist)
black = [b for b in blacklist if b >= self.bound]
w = self.bound
self.rdict = {}
for b in blacklist:
if b < self.bound:
while w in black:
w += 1
self.rdict[b] = w
w += 1
def pick(self) -> int:
rd = randint(0, self.bound-1)
return self.rdict.get(rd, rd)
# Your Solution object will be instantiated and called as such:
# obj = Solution(n, blacklist)
# param_1 = obj.pick()
1252. 奇数值单元格的数目
题目
给你一个 m x n 的矩阵,最开始的时候,每个单元格中的值都是 0。
另有一个二维索引数组 indices,indices[i] = [ri, ci] 指向矩阵中的某个位置,其中 ri 和 ci 分别表示指定的行和列(从 0 开始编号)。
对 indices[i] 所指向的每个位置,应同时执行下述增量操作:
ri 行上的所有单元格,加 1 。
ci 列上的所有单元格,加 1 。
给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后,返回矩阵中 奇数值单元格 的数目。
示例 1:
输入:m = 2, n = 3, indices = [[0,1],[1,1]]
输出:6
解释:最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]],里面有 6 个奇数。
示例 2:
输入:m = 2, n = 2, indices = [[1,1],[0,0]]
输出:0
解释:最后的矩阵是 [[2,2],[2,2]],里面没有奇数。
提示:
1 <= m, n <= 50
1 <= indices.length <= 100
0 <= ri < m
0 <= ci < n
进阶:你可以设计一个时间复杂度为 O(n + m + indices.length) 且仅用 O(n + m) 额外空间的算法来解决此问题吗?
视频
LeetCode刷题实录——Python模拟题的空间优化,1252. 奇数值单元格的数目
代码
class Solution:
def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int:
# 方法1:用模拟的方式,但是这样太简单,并且复杂度较高
# 方法2:记录每行增加次数和每列增加次数,遍历每个格子
# 这里我将使用方法二
row = [0] * m
col = [0] * n
for r, c in indices:
row[r] += 1
col[c] += 1
# 这里还可以做些修改, 修改后时间和空间都有优化
return sum((r+c) % 2 for r in row for c in col)
1260. 二维网格迁移
题目
给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。
每次「迁移」操作将会引发下述活动:
位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。
请你返回 k 次迁移操作后最终得到的 二维网格。
示例 1:
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[9,1,2],[3,4,5],[6,7,8]]
示例 2:
输入:grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
输出:[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]
示例 3:
输入:grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
输出:[[1,2,3],[4,5,6],[7,8,9]]
提示:
m == grid.length
n == grid[i].length
1 <= m <= 50
1 <= n <= 50
-1000 <= grid[i][j] <= 1000
0 <= k <= 100
视频
LeetCode刷题实录——数组存储方式的转换,1260. 二维网格迁移
代码
class Solution:
def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
# 所谓的移动其实是坐标的转换,这里类似于数据结构数组那一块讲的二维转一维,
# 转成一维之后整体移动k位即可
m, n = len(grid), len(grid[0]) # 行列长度
ans = [[0] * n for _ in range(m)] # m行n列的0数组
# 下面根据行列进行行优先的二维转一维
for i in range(m):
for j in range(n):
idx = i * n + j # 这里验证一下,i=2,j=2时, idx = 2 * m + 2,1维中第2 * m + 2位
# print(idx)
idx += k # 加k位
idx = idx % (m * n) # 越界之后回到0,从头开始
# print(idx, m, n)
ans[idx // n][idx % n] = grid[i][j] # 这里还是越界了
return ans
757. 设置交集大小至少为2
一个整数区间 [a, b] ( a < b ) 代表着从 a 到 b 的所有连续整数,包括 a 和 b。
给你一组整数区间intervals,请找到一个最小的集合 S,使得 S 里的元素与区间intervals中的每一个整数区间都至少有2个元素相交。
输出这个最小集合S的大小。
示例 1:
输入: intervals = [[1, 3], [1, 4], [2, 5], [3, 5]]
输出: 3
解释:
考虑集合 S = {2, 3, 4}. S与intervals中的四个区间都有至少2个相交的元素。
且这是S最小的情况,故我们输出3。
示例 2:
输入: intervals = [[1, 2], [2, 3], [2, 4], [4, 5]]
输出: 5
解释:
最小的集合S = {1, 2, 3, 4, 5}.
注意:
intervals 的长度范围为[1, 3000]。
intervals[i] 长度为 2,分别代表左、右边界。
intervals[i][j] 的值是 [0, 10^8]范围内的整数。
class Solution:
def intersectionSizeTwo(self, intervals: List[List[int]]) -> int:
# 贪心算法,具体思路就是找到一段一定要有的区间然后去拓展,要拓展我们就需要先排序
# 按照a递增,b递减排序,最后一个的前两个元素的区间一定选用
# 以第一个例子为例
'''
1 2 3
1 2 3 4
2 3 4 5
3 4 5
在这里3,4一定选用,然后向前遍历,不够2个交集的拓展范围就好
'''
# 这里我忽略了题目的条件,本来应该是集合,我这个做法是连续的序列
# 不过贪心的思路没有变
# 这里也列一下现在这个用例
'''
2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 11 12 13 14
3 4 5 6 7
4 5 6 7 8 9 10 11
6 7 8 9 10 11 12 13 14 15
6 7 8 9 10 11 12
7 8 9 10 11
7 8
11 12
'''
intervals.sort(key=lambda x:(x[0], -x[1]))
length = len(intervals)
vals = [[] for _ in range(length)] # 用来存储每个区间(intervals)为了保证存在两个的必选值
ans = 0
for i in range(length-1, -1, -1):
# 依然倒着遍历
low = intervals[i][0] # 每一个遍历到的最低位
for j in range(len(vals[i]), 2): # 当第i个必选值少于2个时进入循环
ans += 1 # 因为必选的少于2,所以可选,所以选择当前的最低的,ans=ans+1
# 整体更新 vals
for k in range(i-1, -1, -1):
# 如果low在区间内加入该区间的vals
if intervals[k][1] < low:
break
vals[k].append(low)
low += 1
return ans
END
谢谢大家,未完待更,可私心催更