机器学习强基计划3-4：详解核方法——以核支持向量机KVSM为例

0 写在前面

机器学习强基计划聚焦深度和广度，加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理；“广”在分析多个机器学习模型：决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。

详情：机器学习强基计划(附几十种经典模型源码合集)

1 为什么需要核方法？

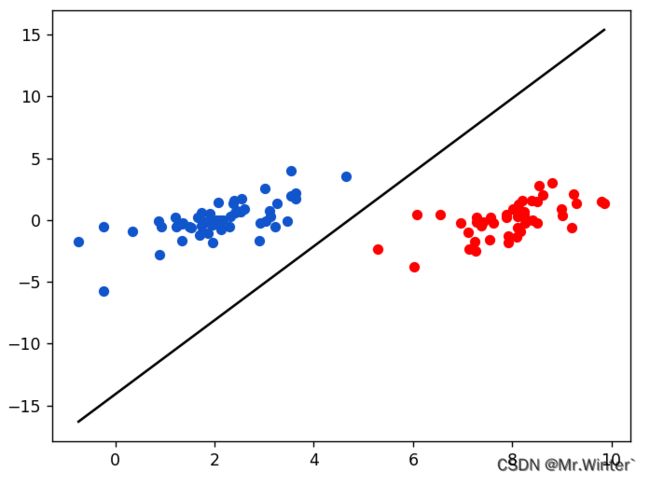
说到核方法必须介绍一下线性可分的概念。所谓线性可分就是在$n$维特征空间中可以用$n-1$维超平面划分开正、负两个样本集，例如下图所示采用一条直线分开了二维平面上的正负样本

但现实情况下并非所有的数据都是线性可分的，比如

这种情况采用线性的机器学习模型，比如SVM是不可能取得很好的泛化能力的。这时候我们就思考：线性不可分的样本在其他维度的投影难道也是不可分的吗？

幸运的是，有这样一个定理

定理：若原始样本空间是有限维，则必存在一个高维特征空间使样本线性可分。

也就是说，理论上总存在划分超平面$\pi :{\mathbf{w}}^T\varphi \left(\mathbf{x}\right)+b=0$，其中$\varphi \left(\cdot \right)$是原始样本空间$\mathcal{X}$到高维特征空间$\mathcal{F}$的映射。比如之前线性不可分的样本集，在投影到更高维度的空间后就具有线性可分的性质。核方法就是一类把低维空间的非线性可分问题，转化为高维空间的线性可分问题的方法。

2 常用核函数总结

在实际问题中，由于不知晓怎样的$\mathcal{F}$是合适的高维特征空间，即无法显式地确定$\varphi \left(\cdot \right)$，因此引入核函数(Kernel Function)

$$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=⟨\varphi \left({\mathbf{x}}_i\right),\varphi \left({\mathbf{x}}_j\right)⟩=\varphi {\left({\mathbf{x}}_i\right)}^T\varphi \left({\mathbf{x}}_j\right)$$

常见的核函数如表所示

名称	表达式
线性核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={{\mathbf{x}}_i}^T{\mathbf{x}}_j$
多项式核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left({{\mathbf{x}}_i}^T{\mathbf{x}}_j\right)}^d$
高斯核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{{|{\mathbf{x}}_i-{\mathbf{x}}_j|}_2^2}{2{\sigma }^2}\right)$
拉普拉斯核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\exp \left(-\frac{|{\mathbf{x}}_i-{\mathbf{x}}_j|}{\sigma }\right)$
Sigmoid核	$\kappa \left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\tanh \left(\beta {{\mathbf{x}}_i}^T{\mathbf{x}}_j+\theta \right)$

核函数不仅可以隐式地将$\mathcal{X}$映射到高维特征空间$\mathcal{F}$，还可以避免直接计算$\varphi {\left({\mathbf{x}}_i\right)}^T\varphi \left({\mathbf{x}}_j\right)$，因为$\varphi \left(\mathbf{x}\right)$的维度可能很高而引发维数灾难。比如对于线性核

$$\varphi {\left({\mathbf{x}}_i\right)}^T\varphi \left({\mathbf{x}}_j\right)={{\mathbf{x}}_i}^T{\mathbf{x}}_j$$

即高维映射后的样本内积和低维空间中的情况完全一致——因为是线性映射。

有一个问题是：凭什么高维线性可分空间的样本，其内积符合核函数的定义？

所以，核函数的缺陷在于不可解释$\varphi \left(\cdot \right)$，可能将$\mathcal{X}$映射到不合适的$\mathcal{F}$导致模型性能的下降和振荡。对于同一个数据集，应用不同的核函数投影，最终的准确率大概率是不一致的，可能这个数据集符合高斯核函数的投影，而另一个数据集更适应拉普拉斯函数。

3 KSVM的python实现

3.1 设计核函数

在详细推导序列最小优化SMO算法+Python实现中，我们从底层实现了线性软间隔SVM的模型。将其改造为核化SVM很容易：在基类svm_interface中添加一个核函数

def kernel(self, xi, xj):
    xi = xi.reshape(self.d, -1)
    xj = xj.reshape(self.d, -1)
    if self.kernelType == 'linear':
        res = np.dot(xi.T, xj)
        if res.size == 1:
            return np.squeeze(res)
        return res   
    elif self.kernelType == 'gauss':
        res = np.exp(-self.gamma * np.sum((xi - xj)**2, axis=0, keepdims=True)).T
        if res.size == 1:
            return np.squeeze(res)
        return res

这里只实现了线性核与高斯核

3.2 KSVM与SVM的对比

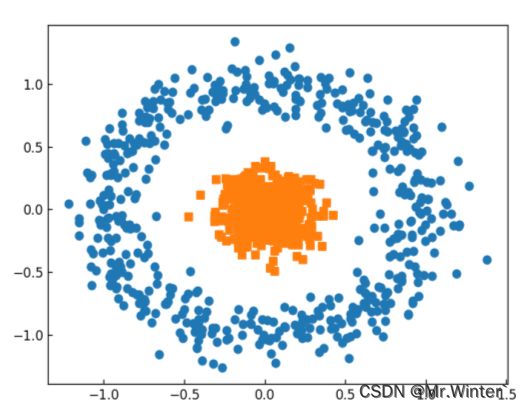
针对如下所示的线性不可分数据集

使用KSVM的预测准确率为

model = SVM_HEURISTIC(X, y, kernel='gauss', gamma=1.2)
model.train()
model.show()

>>> 准确率为0.97

使用SVM的预测准确率为

model = SVM_HEURISTIC(X, y)
model.train()
model.show()

>>> 准确率为0.6

完整源码请联系下方博主名片获取

---

更多精彩专栏：

• 《ROS从入门到精通》
• 《机器人原理与技术》
• 《机器学习强基计划》
• 《计算机视觉教程》
• …

源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系