A8.2022年全国数学建模竞赛 B题-无人机编队飞行定位问题-赛题分析与讨论
2022年全国数学建模竞赛 B题-赛题分析与讨论
**说明:本文于 2022/9/15 22:00 第一次更新, 2022/9/16 12:00 第二次更新,建议收藏.**
文章目录
- 2022年全国数学建模竞赛 B题-赛题分析与讨论
-
- 1. 2022年B题(无人机遂行编队飞行中的纯方位无源定位)
- 2. 算法讨论
-
- 2.1 规划问题+选址问题,问题1 推荐采用极坐标,问题2推荐采用直角坐标
- 2.2 规划问题参考例程
-
- PuLP 程序 1:
- PuLP 程序 2:使用 LpVariable 逐一定义变量
- 2.3 选址问题参考例程
-
- 选址问题 Python 例程
- 4.4 Python 例程运行结果
- 3. 参考文献
-
- [1]邹先雄. 无人机目标无源定位方法研究[D].电子科技大学,2018.
- [2]屈小媚,刘韬,谈文蓉.基于多无人机协作的多目标无源定位算法[J].中国科学:信息科学,2019,49(05):570-584.
- [3]王仁军. 基于UWB定位的无人机集群系统[D].杭州电子科技大学,2019.
- [4]李晓辉,方坤,樊韬,刘佳文,吕思婷.基于支持向量机的无人机定位信号分离算法研究[J].电子与信息学报,2021,43(09):2601-2607.
1. 2022年B题(无人机遂行编队飞行中的纯方位无源定位)
B题 无人机遂行编队飞行中的纯方位无源定位
无人机集群在遂行编队飞行时,为避免外界干扰,应尽可能保持电 磁静默,少向外发射电磁波信号。
为保持编队队形,拟采用纯方位无源定位的方法调整无人机的位置,即由编队中某几架无人机发射信号,其余无人机被动接收信号,从中提取出方向信息进行定位,来调整无人机的位置。
2. 算法讨论
2.1 规划问题+选址问题,问题1 推荐采用极坐标,问题2推荐采用直角坐标
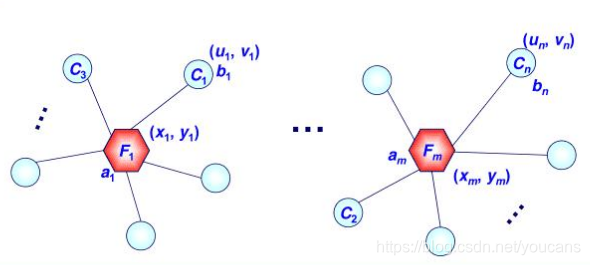
2.2 规划问题参考例程
Python数模笔记-PuLP库(1)线性规划入门 PuLP库(1)线性规划入门
Python数模笔记-PuLP库(2)线性规划进阶 PuLP库(2)线性规划进阶
Python数模笔记-PuLP库(2)线性规划进阶 PuLP库(3)线性规划实例
PuLP 程序 1:
import pulp # 导入 pulp库
ProbLP2 = pulp.LpProblem("ProbLP2", sense=pulp.LpMaximize) # 定义问题 2,求最大值
x1 = pulp.LpVariable('x1', lowBound=0, upBound=8, cat='Continuous') # 定义 x1
x2 = pulp.LpVariable('x2', lowBound=0, upBound=7.5, cat='Continuous') # 定义 x2
x3 = pulp.LpVariable('x3', cat='Continuous') # 定义 x3
ProbLP2 += (10*x1 + 9*x2 - x3) # 设置目标函数 f(x)
ProbLP2 += (6*x1 + 5*x2 - 1.25*x3 <= 60) # 不等式约束
ProbLP2 += (10*x1 + 20*x2 <= 150) # 不等式约束
ProbLP2.solve()
print(ProbLP2.name) # 输出求解状态
print("Status:", pulp.LpStatus[ProbLP2.status]) # 输出求解状态
for v in ProbLP2.variables():
print(v.name, "=", v.varValue) # 输出每个变量的最优值
print("F2(x)=", pulp.value(ProbLP2.objective)) # 输出最优解的目标函数值
PuLP 程序 2:使用 LpVariable 逐一定义变量
本程序与上篇的方法相同,使用 LpVariable 逐一定义变量。完整的程序代码如下:
import pulp # 导入 pulp库
# 1.建立优化问题 AlloyLP: 求最小值(LpMinimize)
AlloyLP = pulp.LpProblem("合金生产材料优化", sense=pulp.LpMinimize) # 定义问题,求最小值
# 2.定义决策变量 x1~x7
x1 = pulp.LpVariable('废料1#', lowBound=0, upBound=75.0, cat='Continuous') # 定义 x1
x2 = pulp.LpVariable('废料2#', lowBound=0, upBound=250., cat='Continuous') # 定义 x2
x3 = pulp.LpVariable('废料3#', lowBound=0, cat='Continuous') # 定义 x3
x4 = pulp.LpVariable('废料4#', lowBound=0, cat='Continuous') # 定义 x4
x5 = pulp.LpVariable('原料镍', lowBound=0, cat='Continuous') # 定义 x5
x6 = pulp.LpVariable('原料铬', lowBound=0, cat='Continuous') # 定义 x6
x7 = pulp.LpVariable('原料钼', lowBound=0, cat='Continuous') # 定义 x7
# 3.定义目标函数 cost
AlloyLP += (16*x1 + 10*x2 + 8*x3 + 9*x4 + 48*x5 + 60*x6 + 53*x7) # 投料成本
# 4.设置约束条件
AlloyLP += (x1 + x2 + x3 + x4 + x5 + x6 + x7 == 1000) # 等式约束
AlloyLP += (0.8*x1 + 0.7*x2 + 0.85*x3 + 0.4*x4 >= 0.65*1000) # 不等式约束
AlloyLP += (0.8*x1 + 0.7*x2 + 0.85*x3 + 0.4*x4 <= 0.75*1000) # 不等式约束
AlloyLP += (18.0*x1 + 3.2*x2 + 100.0*x5 >= 3.0*1000) # 不等式约束
AlloyLP += (18.0*x1 + 3.2*x2 + 100.0*x5 <= 3.5*1000) # 不等式约束
AlloyLP += (12.0*x1 + 1.1*x2 + 100.0*x6 >= 1.0*1000) # 不等式约束
AlloyLP += (12.0*x1 + 1.1*x2 + 100.0*x6 <= 1.2*1000) # 不等式约束
AlloyLP += (0.1*x2 + 100.0*x7 >= 1.1*1000) # 不等式约束
AlloyLP += (0.1*x2 + 100.0*x7 <= 1.3*1000) # 不等式约束
AlloyLP += (x1 + x2 + x3 + x4 + x5 + x6 + x7 == 1000) # 等式约束
# 5.求解线性规划问题
AlloyLP.solve()
# 6.输出优化结果
print(AlloyLP) # 输出问题设定参数和条件
# print("求解状态:", pulp.LpStatus[AlloyLP.status]) # 输出求解状态
for v in AlloyLP.variables():
print(v.name, " = ", v.varValue) # 输出每个变量的最优值
print("最小材料成本 = ", pulp.value(AlloyLP.objective)) # 输出最优解的目标函数值
# = 关注 Youcans,分享原创系列 https://blog.csdn.net/youcans =
2.3 选址问题参考例程
Python小白的数学建模课-07.选址问题 Python小白的数学建模课-07.选址问题
选址问题 Python 例程
# mathmodel09_v1.py
# Demo08 of mathematical modeling algorithm
# Solving set covering problem with PuLP.
# Copyright 2021 Youcans, XUPT
# Crated:2021-06-06
# Python小白的数学建模课 @ Youcans
import pulp # 导入 pulp 库
# 主程序
def main():
# 问题建模:
"""
决策变量:
x(j) = 0, 不选择第 j 个消防站
x(j) = 1, 选择第 j 个消防站, j=1,8
目标函数:
min fx = sum(x(j)), j=1,8
约束条件:
sum(x(j)*R(i,j),j=1,8) >=1, i=1,8
变量取值范围:
x(j) = 0,1
"""
# 消防站的选址问题 (set covering problem, site selection of fire station)
# 1.建立优化问题 SetCoverLP: 求最小值(LpMinimize)
SetCoverLP = pulp.LpProblem("SetCover_problem_for_fire_station", sense=pulp.LpMinimize) # 定义问题,求最小值
# 2. 建立变量
zones = list(range(8)) # 定义各区域 youcans
x = pulp.LpVariable.dicts("zone", zones, cat="Binary") # 定义 0/1 变量,是否在该区域设消防站
# 3. 设置目标函数
SetCoverLP += pulp.lpSum([x[j] for j in range(8)]) # 设置消防站的个数
# 4. 施加约束
reachable = [[1, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 1, 0, 0, 0, 0, 0],
[0, 1, 1, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 1, 1]] # 参数矩阵,第 i 消防站能否在 10分钟内到达第 j 区域
for i in range(8):
SetCoverLP += pulp.lpSum([x[j]*reachable[j][i] for j in range(8)]) >= 1
# 5. 求解
SetCoverLP.solve()
# 6. 打印结果
print(SetCoverLP.name)
temple = "区域 %(zone)d 的决策是:%(status)s" # 格式化输出
if pulp.LpStatus[SetCoverLP.status] == "Optimal": # 获得最优解
for i in range(8):
output = {'zone': i+1, # 与问题中区域 1~8 一致
'status': '建站' if x[i].varValue else '--'}
print(temple % output)
print("需要建立 {} 个消防站。".format(pulp.value(SetCoverLP.objective)))
return
if __name__ == '__main__': # Copyright 2021 YouCans, XUPT
main() # Python小白的数学建模课 @ Youcans
4.4 Python 例程运行结果
Welcome to the CBC MILP Solver
Version: 2.9.0
Build Date: Feb 12 2015
Result - Optimal solution found
SetCover_problem_for_fire_station
区域 1 的决策是:建站
区域 2 的决策是:--
区域 3 的决策是:建站
区域 4 的决策是:建站
区域 5 的决策是:--
区域 6 的决策是:建站
区域 7 的决策是:建站
区域 8 的决策是:--
需要建立 5.0 个消防站
3. 参考文献
[1]邹先雄. 无人机目标无源定位方法研究[D].电子科技大学,2018.
摘要:近年来,无人机行业迅猛发展。在无人机为人们带来便利的同时,也成为了不法分子手中的犯罪工具。对无人机实现管制已经势在必行,而管制的前提是能够对黑飞无人机实现精确定位。基于无源定位的方法具有抗干扰能力强,可以全天候工作,在无人机起飞前就能实现对无人机和操作手的定位等诸多优点。首先,本文对跳频通信进行了理论研究,并在实验室采集无人机信号(包括控制信号和图传信号)进行分析。然后,结合无人机的特点,本文研究了交叉定位算法和无源定位算法在较小区域(一般考虑半径为2000m)内对无人机的定位性能。实现精确的交叉定位的前提是多个测向基站测得无人机准确方位角(和俯仰角),然后通过定位算法解得无人机的平面(或空间)坐标。接下来,本文研究了幅度搜索法测向、全向振幅单脉冲测向、相位干涉仪测向、相关干涉仪测向和空间谱测向五种常用测向算法在小区域内对无人机的测向性能,并对影响每种测向算法测向精度的因素进行了仿真分析。在总结分析上述算法的优劣之后,本文提出基于微带天线的幅度比值查表法测向。对FFT变换、包络检波和直接平均三种幅度提取算法进行仿真分析以确定最佳的幅度提取算法,并对算法的可行性进行了验证,为工程实现提供理论技术准备。最后,本文对二维平面、三维空间下的双站、多站交叉定位分别进行了分析仿真,对影响定位精度的因素也做了仿真研究,并对二维平面双站定位的模糊区域面积,二维平面、三维空间交叉定位精度的GDOP都进行了研究。本文在分析了无源时差定位的定位原理之后,对常用的Chan定位算法和Taylor定位算法进行了分析及仿真,验证了其定位能力。并以Chan算法为基础进行了不同布站方式下的定位精度的GDOP的仿真分析。现阶段,对无人机跳频信号进行时差估计的精度难以保证,以及在小区域内采用时差定位对时差测量精度要求更为苛刻。结合以上研究,本文认为现阶段在实际工程中采用交叉定位成本更低,系统实现更容易,精度也可以得到保证。
[2]屈小媚,刘韬,谈文蓉.基于多无人机协作的多目标无源定位算法[J].中国科学:信息科学,2019,49(05):570-584.
基于多无人机协作的无源目标定位是无人机在军事侦察等领域应用的关键技术.现有研究大部分针对单目标的无源定位,本文研究利用到达时间差观测对多目标进行无源定位的高效算法.将已有的两步加权最小二乘方法中辅助变量与目标位置的非线性关系作为约束,建立约束加权最小二乘多目标定位模型,并化简为含多个二次不定等式约束的二次规划问题.这是一个NP-hard的非凸优化问题.本文提出一种CWLS (constrained weighted least squares)近似迭代算法,在迭代过程中用线性等式约束近似二次不定等式约束,使其近似优化问题有解析解.理论分析表明,该算法收敛的极限一定是原问题的全局最优解. Monte Carlo实验表明,该算法在绝大部分情况下能快速收敛,且对多目标定位的精度优于两步加权最小二乘方法.
[3]王仁军. 基于UWB定位的无人机集群系统[D].杭州电子科技大学,2019.
摘要:随着无人机技术的日趋成熟,无人机应用趋势逐渐由单机执行任务转为多机协同执行任务,朝着集群化的方向快速发展,并在军事和民用领域都呈现出广阔的应用前景。而无人机集群的关键技术点在于实现无人机的精确定位,目前多数采用GNSS或双目视觉的定位方案。但在复杂的室内场景中,仍很难获取到高精度、高稳定性的定位信息。因此,本文对UWB定位和无人机集群编队技术进行了研究,提出了基于UWB定位的无人机集群系统方案,并软硬件全自主设计了适用于UWB定位的微型四旋翼无人机,搭建了无人机集群编队平台。主要包含如下几个方面的内容:(1)对UWB的技术特点进行了分析,尤其是在无人机定位方面的优势,研究了几种常用的UWB定位方法,并结合无人机应用场景,提出了基于RTOF定位方法的优化方案。(2)分析几种常用的无线组网通信技术,提出了一种适用于微型无人机的WiFi自适应组网通信方案,并通过实验验证了方案的有效性。(3)主要研究了无人机的运动模型和集群编队模型。针对无人机编队形成与保持问题,研究了优化人工势场算法应用于无人机集群编队的可行性,仿真验证了该方法能够保证无人机编队在虚拟无人机的带领下,完成跟踪其轨迹并保持稳定的队形。(4)软硬件全自主设计了适用于UWB定位的微型四旋翼无人机,研究了无人机的姿态解算算法和PID控制算法,为基于UWB定位的无人机集群研究提供平台基础。(5)从无人机的基本飞行功能、空间定位效果、集群编队三个方面进行了系统综合测试与分析,验证方案的可行性。本文通过对无人机集群编队技术的研究和分析,有针对性的提出了基于UWB的室内定位解决方案。经过大量的测试验证,该方案具有高可靠和高精度的特性,对室内环境下无人机集群研究提供了一定的参考价值。
[4]李晓辉,方坤,樊韬,刘佳文,吕思婷.基于支持向量机的无人机定位信号分离算法研究[J].电子与信息学报,2021,43(09):2601-2607.
摘要:为了解决无人机(UAV)无源定位中难以从多径干扰严重的环境中提取无人机定位信号的问题,该文提出一种基于支持向量机(SVM)的无人机定位信号分离算法,在SVM模型训练时,通过计算无人机相邻数据集之间的欧氏距离获取信息熵,为SVM映射高维空间提供模型数据。在此基础上,加入映射函数阈值软边界,使模型具有参数自适应调整能力,来适应无人机运动灵活所导致的数据差异。最后构建了观测者操作特性曲线获取无人机定位信号分离结果。仿真结果表明所提算法能够有效分离无人机定位信号与噪声,在多径干扰严重的情况下具有较高的信号分离准确率。