语音信号处理-python

语音信号处理

1.语音信号的产生与特性

我们要对语音进行分析，首先要提取能够表示该语音的特征参数，有了特征参数才可能利用这些参数进行有效的处理，在对语音信号处理的过程中，语音信号的质量不仅取决于处理方法，同时取决于时候选对了合适的特征参数。

语音信号是一个非平稳的时变信号，但语音信号是由声门的激励脉冲通过声道形成的，而声道(人的口腔、鼻腔)的肌肉运动是缓慢的，所以“短时间”(10~30ms)内可以认为语音信号是平稳时不变的。由此构成了语音信号的“短时分析技术”。

提取的不同的语音特征参数对应着不同的语音信号分析方法：时域分析、频域分析、倒谱域分析…由于语音信号最重要的感知特性反映在功率谱上，而相位变化只起到很小的作用，所有语音频域分析更加重要。

2.语音的读取

本实验使用wave库，实现语音文件的读取、波形图绘制，相关的库还有librosa、scipy等

import wave #调用wave模块
import matplotlib.pyplot as plt #调用matplotlib.pyplot模块作为Plt
import numpy as np  #调用numpy模块记作np
import scipy.signal as signal
import pyaudio

%matplotlib inline
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

f = wave.open(r"C:\Users\zyf\Desktop\Jupyter\1.wav", "rb")#读取语音文件
params = f.getparams() #返回音频参数
nchannels, sampwidth, framerate, nframes = params[:4] #赋值声道数，量化位数，采样频率，采样点数
print(nchannels,sampwidth,framerate,nframes)# 输出声道数，量化位数，采样频率，采样点数

str_data = f.readframes(nframes) # 读取nframes个数据，返回字符串格式
f.close()
wave_data = np.frombuffer(str_data, dtype=np.short) # 将字符串转换为数组，得到一维的short类型的数组
wave_data = wave_data * 1.0 / (max(abs(wave_data))) # 赋值的归一化
time = np.arange(0, nframes) * (1.0 / framerate) # 最后通过采样点数和取样频率计算出每个取样的时间
# 整合左声道和右声道的数据,如果语音为双通道语音，具体代码需做调整
#wave_data = np.reshape(wave_data, [nframes, nchannels])
# wave_data.shape = (-1, 2)   # -1的意思就是没有指定,根据另一个维度的数量进行分割
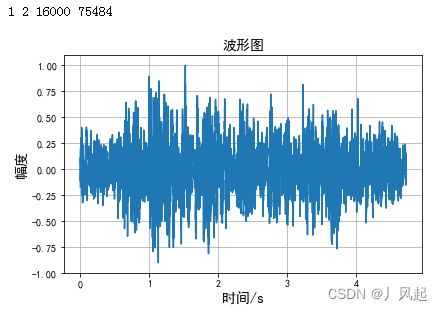
plt.figure() # 单通道语音波形图
plt.plot(time, wave_data[:])
plt.xlabel("时间/s",fontsize=14)
plt.ylabel("幅度",fontsize=14)
plt.title("波形图",fontsize=14)
plt.grid()  # 标尺

plt.tight_layout()  # 紧密布局
plt.show()

3.语音的播放

# 音频的播放，本实验使用pyaudio（代码相对matlab较麻烦，后期简化）
import pyaudio
import wave

chunk = 1024
wf = wave.open(r"C:\Users\zyf\Desktop\Jupyter\1.wav", 'rb')
p = pyaudio.PyAudio()

# 打开声音输出流
stream = p.open(format = p.get_format_from_width(wf.getsampwidth()),
                channels = wf.getnchannels(),
                rate = wf.getframerate(),
                output = True)

# 写声音输出流到声卡进行播放
while True:
    data = wf.readframes(chunk)
    if data == "":
        break
    stream.write(data)

stream.stop_stream()
stream.close()
p.terminate()   # 关闭PyAudio

4.音频文件的写入

# 音频文件的写入、存储
# 使用wave库，相关的库还有librosa、scipy等，读写操作上的差异参阅博客： https://blog.csdn.net/weixin_38346042/article/details/119906391
import wave
import numpy as np
import scipy.signal as signal

framerate = 44100   # 采样频率
time = 10           # 持续时间

t = np.arange(0, time, 1.0/framerate)

# 调用scipy.signal库中的chrip函数，
# 产生长度为10秒、取样频率为44.1kHz、100Hz到1kHz的频率扫描波
wave_data = signal.chirp(t, 100, time, 1000, method='linear') * 10000

# 由于chrip函数返回的数组为float64型，
# 需要调用数组的astype方法将其转换为short型。
wave_data = wave_data.astype(np.short)

# 打开WAV音频用来写操作
f = wave.open(r"sweep.wav", "wb")

f.setnchannels(1)           # 配置声道数
f.setsampwidth(2)           # 配置量化位数
f.setframerate(framerate)   # 配置取样频率
comptype = "NONE"
compname = "not compressed"

# 也可以用setparams一次性配置所有参数
# outwave.setparams((1, 2, framerate, nframes,comptype, compname))

# 将wav_data转换为二进制数据写入文件
f.writeframes(wave_data.tobytes())
f.close()

5.语音的分帧加窗

5.1 分帧

语音数据和视频数据不同，本没有帧的概念，但是为了传输与存储，我们采集的音频数据都是一段一段的。为了程序能够进行批量处理，会根据指定的长度（时间段或者采样数）进行分段，结构化为我们编程的数据结构，这就是分帧。语音信号在宏观上是不平稳的，在微观上是平稳的，具有短时平稳性（10—30ms内可以认为语音信号近似不变），这个就可以把语音信号分为一些短段来进行处理，每一个短段称为一帧（CHUNK）。

5.2 帧移

由于我们常用的信号处理方法都要求信号是连续的，也就说必须是信号开始到结束，中间不能有断开。然而我们进行采样或者分帧后数据都断开了，所以要在帧与帧之间保留重叠部分数据，以满足连续的要求，这部分重叠数据就是帧移。

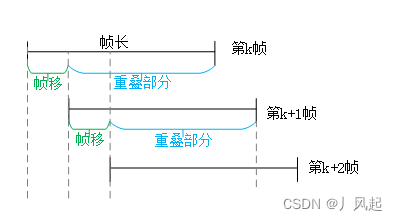
帧长=重叠+帧移

5.3 加窗

我们处理信号的方法都要求信号是连续条件，但是分帧处理的时候中间断开了，为了满足条件我们就将分好的帧数据乘一段同长度的数据，这段数据就是窗函数整个周期内的数据，从最小变化到最大，然后最小。

常用的窗函数：矩形窗、汉明窗、海宁窗
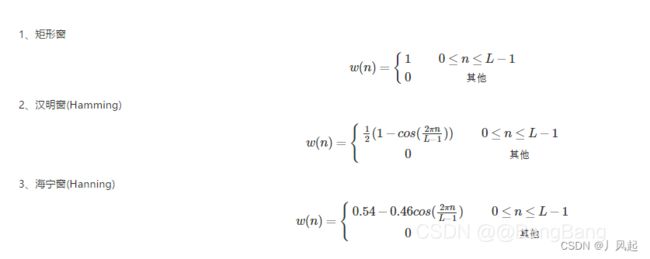加窗即与一个窗函数相乘,加窗之后是为了进行傅里叶展开.
1.使全局更加连续，避免出现吉布斯效应
2.加窗时候，原本没有周期性的语音信号呈现出周期函数的部分特征。
加窗的代价是一帧信号的两端部分被削弱了，所以在分帧的时候，帧与帧之间需要有重叠。

# 加窗分帧（接上）
# 语音分帧、加窗
wlen=512 # 每帧信号长度
inc=128  # 帧移
signal_length=len(wave_data) #信号总长度
print(signal_length)
if signal_length<=wlen: #若信号长度小于一个帧的长度，则帧数定义为1
        nf=1
else:                 #否则，计算帧的总长度
        nf=int(np.ceil((1.0*signal_length-wlen+inc)/inc))   # nf 为帧数
# np.ceil向上取整，所以会导致实际分帧后的长度大于信号本身的长度，所以要对原来的信号进行补零
pad_length=int((nf-1)*inc+wlen) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补，类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,wlen),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(wlen,1)).T  #相当于对所有帧的时间点进行抽取，得到nf*wlen长度的矩阵
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号,587*512的矩阵信号
#a=frames[30:31]
#print(frames.shape)
winfunc = signal.hamming(wlen) # 调用窗函数，本初以汉明窗为例
#print(winfunc.shape) 
win=np.tile(winfunc,(nf,1)) #窗函数为一维数组（512，），因此需要按照信号帧数进行变换得到（587*512）矩阵信号
#print(win.shape)
my = frames*win   # 这里的*指的是计算矩阵的数量积（即对位相乘）。
# python中矩阵运算分为两种形式，一是np.array，而是np.matrix
# ----------------------------------
#  绘制分帧加窗后的图像（接上）
# 因为分帧加窗后的信号为587*512的矩阵信号，为了绘图，将其转换为一维信号
t=my.flatten()  
t=t.T
print(t.shape)
time = np.arange(0, len(t)) * (1.0 / framerate)   # 调整时间轴
plt.figure()
plt.plot(time,t,c="g")
plt.grid()
plt.show()

6.语音的频谱分析

6.1 频谱图

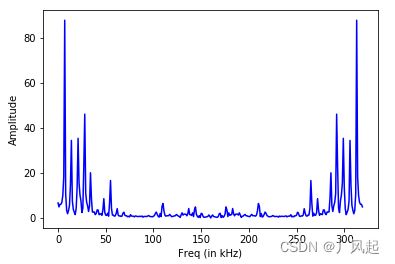
通过FFT对时域语音信号进行处理，得到频谱图

import numpy as np
from scipy.io import wavfile
import matplotlib.pyplot as plt

%matplotlib inline
sampling_freq, audio = wavfile.read(r"C:\Users\zyf\Desktop\Jupyter\1.wav")   # 读取文件

audio = audio / np.max(audio)   # 归一化，标准化

# 应用傅里叶变换
fft_signal = np.fft.fft(audio)
print(fft_signal)

fft_signal = abs(fft_signal)
print(fft_signal)

# 建立时间轴
Freq = np.arange(0, len(fft_signal))

# 绘制语音信号的
plt.figure()
plt.plot(Freq, fft_signal, color='blue')
plt.xlabel('Freq (in kHz)')
plt.ylabel('Amplitude')
plt.show()

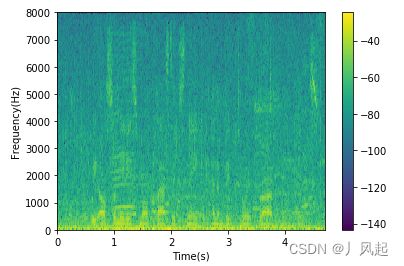
6.2 语谱图

语谱图综合了时域和频域的特点，明显的显示出来了语音频率随时间的变化情况**，语谱图的横轴为时间，纵轴为频率任意给定频率成分在给定时刻的强弱用颜色深浅表示。**颜色深表示频谱值大，颜色浅表示频谱值小，谱图上不同的黑白程度形成不同的纹路，称为声纹，不用讲话者的声纹是不一样的，可以用做声纹识别。

import wave
import matplotlib.pyplot as plt
import numpy as np

f = wave.open(r"C:\Users\zyf\Desktop\Jupyter\1.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
strData = f.readframes(nframes)#读取音频，字符串格式
waveData = np.fromstring(strData,dtype=np.int16)#将字符串转化为int
waveData = waveData*1.0/(max(abs(waveData)))#wave幅值归一化
waveData = np.reshape(waveData,[nframes,nchannels]).T
f.close()

plt.specgram(waveData[0],Fs = framerate, scale_by_freq = True, sides = 'default')
plt.ylabel('Frequency(Hz)')
plt.xlabel('Time(s)')
plt.colorbar()
plt.show()

参考博客：
https://www.cnblogs.com/zhenmeili/p/14830176.html
https://blog.csdn.net/sinat_18131557/article/details/105340416
https://blog.csdn.net/weixin_38346042/article/details/119906391
https://www.jb51.net/article/126984.htm