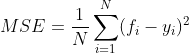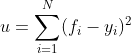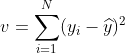【机器学习笔记】【随机森林】【回归器】【填充缺失值】
目录
一、随机森林回归器简介
1.重要的参数、属性、接口
①criterion
2.查看sklearn中所有的打分接口
二、随机森林回归的初次使用
1.导入相关的数据包
2.导入并查看数据集
3.实例化模型并打分
三、实例用随机森林填补缺失值
1.导入所需要的库
2.查看相关的数据信息
3.制造缺失数据
①计算缺失的数量
②创建随机的缺失位置
③生成缺失值
四、不同的数据填补方式
1.使用均值进行填补
①证明缺失值全部填补
2.使用0进行填补
①证明缺失值全部被填补
3.使用随机森林进行缺失值填补
①前置处理
②对特征矩阵的缺失值的多少按列排序
③构建我们新的特征矩阵
④构建训练集和测试集
⑤用随机森林填补缺失值
⑥循环填充
五、比较四种不同的预测效果
1.建模
2.绘图
一、随机森林回归器简介
class sklearn.ensemble.RandomForestRegressor (n_estimators=’warn’
, criterion=’mse’
, max_depth=None
,min_samples_split=2
, min_samples_leaf=1
, min_weight_fraction_leaf=0.0
, max_features=’auto’
,max_leaf_nodes=None
, min_impurity_decrease=0.0
, min_impurity_split=None
, bootstrap=True
, oob_score=False
,n_jobs=None
, random_state=None
, verbose=0
, warm_start=False)
所有的参数,属性与接口,全部和随机森林分类器一致。
仅有的不同就是回归树与分类树的不同,不纯度的指标,参数Criterion不一致。
predict_proba接口返回每个样本点对应每个类别的概率
对于随机森林回归来说没有这个predict_proba接口,为什么?
因为它并不存在说每一个样本被分到某一类标签的概率问题,所以没有这个接口
1.重要的参数、属性、接口
①criterion
回归树衡量分枝质量的指标,支持的标准有三种:
1)输入"mse"使用均方误差mean squared error(MSE),父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准,这种方法通过使用叶子节点的均值来最小化L2损失
2)输入“friedman_mse”使用费尔德曼均方误差,这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
3)输入"mae"使用绝对平均误差MAE(mean absolute error),这种指标使用叶节点的中值来最小化L1损失
其中N是样本数量,i是每一个数据样本,fi是模型回归出的数值,yi是样本点i实际的数值标签。所以MSE的本质,其实是样本真实数据与回归结果的差异。在回归树中,MSE不只是我们的分枝质量衡量指标,也是我们最常用的衡量回归树回归质量的指标,当我们在使用交叉验证,或者其他方式获取回归树的结果时,我们往往选择均方误差作为我们的评估(在分类树中这个指标是score代表的预测准确率)。
在回归中,我们追求的是,MSE越小越好。
然而,回归树的接口score返回的是R平方,并不是MSE。R平方被定义如下:
![]()
其中u是残差平方和(MSE * N),v是总平方和,N是样本数量,i是每一个数据样本,fi是模型回归出的数值,yi是样本点i实际的数值标签。y帽是真实数值标签的平均数。R平方可以为正为负(如果模型的残差平方和远远大于模型的总平方和,模型非常糟糕,R平方就会为负),而均方误差永远为正。值得一提的是,虽然均方误差永远为正,但是sklearn当中使用均方误差作为评判标准时,却是计算”负均方误差“(neg_mean_squared_error)。
这是因为sklearn在计算模型评估指标的时候,会考虑指标本身的性质,均方误差本身是一种误差,所以被sklearn划分为模型的一种损失(loss),因此在sklearn当中,都以负数表示。真正的均方误差MSE的数值,其实就是neg_mean_squared_error去掉负号的数字。
R^2的取值范围是(-∞,1),越接近1的结果越好
MSE本身应该是正的,但是sklearn当中使用均方误差作为评判标准时,却是计算”负均方误
差“(neg_mean_squared_error)真正的均方误差MSE的数值,其实就是neg_mean_squared_error去掉负号的数字。
mse越小越好(正的)
2.查看sklearn中所有的打分接口
import sklearn
#sklearn当中的所有的模型评估指标(打分)列表
sorted(sklearn.metrics.SCORERS.keys())二、随机森林回归的初次使用
1.导入相关的数据包
#随机森林回归的用法
#和决策树完全一致,除了多了参数n_estimators
from sklearn.datasets import load_boston #标签是连续性变量的数据集
#导入交叉验证
from sklearn.model_selection import cross_val_score
#导入随机森林的回归器
from sklearn.ensemble import RandomForestRegressor2.导入并查看数据集
boston = load_boston()
boston3.实例化模型并打分
#实例化随机森林的回归器,构建树的个数为100,随机参数为0
regressor = RandomForestRegressor(n_estimators=100,random_state=0)
#交叉验证
#第一个参数:我们的实例化好的模型
#第二个参数:分训练集和测试集之前的完整的特征矩阵
#第三个参数,完整的标签
#第四个参数:交叉验证的次数
#第五个参数:打分的标准neg_mean_squared_error,如果不写的话默认的打分标准是R^2
cross_val_score(regressor, boston.data, boston.target, cv=10
,scoring = "neg_mean_squared_error")三、实例用随机森林填补缺失值
实例:用随机森林回归填补缺失值
我们从现实中收集的数据,几乎不可能是完美无缺的,往往都会有一些缺失值。面对缺失值,很多人选择的方式是直接将含有缺失值的样本删除,这是一种有效的方法,但是有时候填补缺失值会比直接丢弃样本效果更好,即便我们其实并不知道缺失值的真实样貌。在sklearn中,我们可以使用sklearn.impute.SimpleImputer来轻松地将均值,中值,或者其他最常用的数值填补到数据中,在这个案例中,我们将使用均值,0,和随机森林回归来填补缺失值,并验证四种状况下的拟合状况,找出对使用的数据集来说最佳的缺失值填补方法。
1.导入所需要的库
#1.导入需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#导入波士顿数据集
from sklearn.datasets import load_boston
#用来填补缺失值的类
from sklearn.impute import SimpleImputer
#导入随机森林回归器
from sklearn.ensemble import RandomForestRegressor2.查看相关的数据信息
#2.查看数据的相关信息
dataset = load_boston()
datasetdataset.data.shape
#总共506*13=6578个数据#查看标签
#我们注意到标签已经不再是分类了,这里都是连续性变量的数据
#对于连续性变量的标签,我们需要做回归
dataset.target#查看特征矩阵
dataset.data3.制造缺失数据
#为了验证填补缺失值的准确性
#我们需要在完整的数据集中制造缺失的数据
#X_full和y_full就代表完整的数据集
X_full, y_full = dataset.data, dataset.target#将样本的数量和标签的数量保存出来
n_samples = X_full.shape[0]
n_features = X_full.shape[1]n_samplesn_features①计算缺失的数量
#首先确定我们希望放入的缺失数据的比例,在这里我们假设是50%,那总共就要有3289个数据缺失
#确定一个随机的模式,之后要用到随机的地方全部都可以用rng代替
rng = np.random.RandomState(0)
missing_rate = 0.5
#样本总数 乘上 标签总数 乘上 丢失率,就得到了我们缺失的样本数
#np.floor向下取整,返回.0格式的浮点数
#再用int取整
#n_missing_samples就是丢失的样本的个数
n_missing_samples = int(np.floor(n_samples * n_features * missing_rate))
n_missing_samples②创建随机的缺失位置
#所有数据要随机遍布在数据集的各行各列当中,而一个缺失的数据会需要一个行索引和一个列索引
#如果能够创造一个数组,包含3289个分布在0~506中间的行索引,和3289个分布在0~13之间的列索引,那我们就可以利用索引来为数据中的任意3289个位置赋空值
#然后我们用0,均值和随机森林来填写这些缺失值,然后查看回归的结果如何
#randint(下限,上限,n)请在下限和上限之前取出n个整数
#下面的代码就是从0到13之间,取出3289个整数
#b_feature是我们特征的数目,n_missing_sample是需要求实的样本的个数
missing_features = rng.randint(0,n_features,n_missing_samples)
missing_features#下面的代码是从0到506之间取3289个数据
missing_samples = rng.randint(0,n_samples,n_missing_samples)
missing_samples③生成缺失值
#默认开头是0,请在0到最大值n_samples之间取出n_missing_samples个数值,rapalce=FALSE表示请不要重复
#missing_samples = rng.randint(n_samples,n_missing_samples,replace=False)
#missing_samples = rng.choice(dataset.data.shape[0],n_missing_samples,replace=False)
#我们现在采样了3289个数据,远远超过我们的样本量506,所以我们使用随机抽取的函数randint。但如果我们需要的数据量小于我们的样本量506,
#那我们可以采用np.random.choice来抽样,choice会随机抽取不重复的随机数,因此可以帮助我们让数据更加分散,确保数据不会集中在一些行中
#创造缺失的数据集
#将完整的数据集中的数据拷贝到我们的缺失的数据集中
X_missing = X_full.copy()
y_missing = y_full.copy()
#将我们之前生成的指定位置的数据变成np.nan,也就是缺失值
#也就是missing_samples和missing_features一一对应的位置设置成缺失值
X_missing[missing_samples,missing_features] = np.nan
X_missing#转换成DataFrame是为了后续方便各种操作,numpy对矩阵的运算速度快到拯救人生,但是在索引等功能上却不如pandas来得好用
X_missing = pd.DataFrame(X_missing)
X_missing
#那我们需不需要将y_missing也填充空值呢?
#不可以,特征值可以空,但是我们的标签不能空,空的话,就变成无监督学习了,就变成没有导向的学习了
#但是我们的随机森林还是有监督的学习,是填充我们特征矩阵中的随机值
#所以我们不对y_full做任何操作四、不同的数据填补方式
1.使用均值进行填补
#使用均值进行填补
#SimpleImputer这个类可以用来实现均值填补
from sklearn.impute import SimpleImputer
#第一步,实例化
#第一个参数需要告诉我们的SimpleImputer,我们的缺失值是长什么样子的
#第二个餐胡strategy是策略,也就是我们可以传入mean,也就是均值参数,让其填充均值
imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
#第二部:训练+导出fit+predict,特殊的接口fit_stansform
#将X_missing中所有的值导入到模型里面去计算,计算完毕后填补完均值之后返回回来
X_missing_mean = imp_mean.fit_transform(X_missing)
X_missing_mean①证明缺失值全部填补
#先将array转换为dataframe,不然没办法使用isnull
X_missing_mean=pd.DataFrame(X_missing_mean)
#布尔值为FALSE的话就是0,所以我们可以通过布尔值相加求和,看结果是不是0来知道是不是所有的空值都已经被填充了
X_missing_mean.isnull().sum()2.使用0进行填补
#使用0进行填补
#相比于上面用均值填充,我们这里只需要将strategy也就是策略修改为constant也就是常数,然后后面的fill_value传入我们的常数的数值就可以了
imp_0 = SimpleImputer(missing_values=np.nan, strategy="constant",fill_value=0)
X_missing_0 = imp_0.fit_transform(X_missing)
X_missing_0①证明缺失值全部被填补
X_missing_0=pd.DataFrame(X_missing_mean)
X_missing_0.isnull().sum()3.使用随机森林进行缺失值填补
(有时候你会觉得某种情况下使用均值去填充或者0去填充都不合适,这时候我们就可以使用算法去填充了)
任何回归都是从特征矩阵中学习,然后求解连续型标签y的过程,之所以能够实现这个过程,是因为回归算法认为,特征矩阵和标签之前存在着某种联系。实际上,标签和特征是可以相互转换的,比如说,在一个“用地区,环境,附近学校数量”预测“房价”的问题中,我们既可以用“地区”,“环境”,“附近学校数量”的数据来预测“房价”,也可以反过来,用“环境”,“附近学校数量”和“房价”来预测“地区”。而回归填补缺失值,正是利用了这种思想。
对于一个有n个特征的数据来说,其中特征T有缺失值,我们就把特征T当作标签,其他的n-1个特征和原本的标签组成新的特征矩阵。那对于T来说,它没有缺失的部分,就是我们的Y_test,这部分数据既有标签也有特征,而它缺失的部分,只有特征没有标签,就是我们需要预测的部分。
特征T不缺失的值对应的其他n-1个特征 + 本来的标签:X_train
特征T不缺失的值:Y_train
特征T缺失的值对应的其他n-1个特征 + 本来的标签:X_test
特征T缺失的值:未知,我们需要预测的Y_test
这种做法,对于某一个特征大量缺失,其他特征却很完整的情况,非常适用。
那如果数据中除了特征T之外,其他特征也有缺失值怎么办?
答案是遍历所有的特征,从缺失最少的开始进行填补(因为填补缺失最少的特征所需要的准确信息最少)。填补一个特征时,先将其他特征的缺失值用0代替,每完成一次回归预测,就将预测值放到原本的特征矩阵中,再继续填补下一个特征。每一次填补完毕,有缺失值的特征会减少一个,所以每次循环后,需要用0来填补的特征就越来越少。当进行到最后一个特征时(这个特征应该是所有特征中缺失值最多的),已经没有任何的其他特征需要用0来进行填补了,而我们已经使用回归为其他特征填补了大量有效信息,可以用来填补缺失最多的特征。遍历所有的特征后,数据就完整,不再有缺失值了。
①前置处理
#先生成一份缺失值的拷贝
#reg就代表着regressor也就是用回归填补缺失值
X_missing_reg = X_missing.copy()
X_missing_reg②对特征矩阵的缺失值的多少按列排序
#想要从缺失值最少的那一列开始填补缺失值,首先我们需要知道那一列的缺失值是最少的,需要有一个排序
#找出数据集中,缺失值从小到大排列的特征们的顺序
#axis=0按列进行加和,也就是返回每一列中空值的数量
#(因为我们前面isnull判断是不是缺失值,如果是TRUE的话就是1,所以能够通过sum计算出缺失值的数量)
#所以我们接下来排这些缺失值的顺序就可以了
X_missing_reg.isnull().sum(axis=0)#如果只是简单地使用np.sort,因为这样我们只会得到排序的结果,反而丢失了原来的索引
np.sort(X_missing_reg.isnull().sum(axis=0))#argsort会返回从小到大排序的顺序所对应的索引
#再使用.values将其中的数据取出来
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values
sortindexX_missing_reg.head()③构建我们新的特征矩阵
(这里最后的结果是用循环遍历的形式的,我们这里为了解释,所以拆开了,只去了遍历中的第一次进行解释)
#构建我们的新特征矩阵(没有被选中去填充的特征们+原始的标签)和新标签(被选中去填充的特征)
df = X_missing_reg
#df就是X_missing_reg的拷贝
#因为我们下面需要将非当前要填充空值数据的列的其他的列全部都填充0,
#但是不能对我们原来的矩阵进行填充,因为这样全部填充为0的话,在下一次填充的时候,我们的随机森林根本分辨不出哪些原本是空值
df#构建新标签,这里我们不妨取第6列,因为按照我们之前的排序,第六列是缺失最少的那一列
#利用标签提取,所有的行和第六列的交集
fillc = df.iloc[:,6]
#也就是生成了一个一维数组
fillc#新特征矩阵(也就是原来的特征中没有被选中的特征再加上原有的标签)
#也就是请帮我取出所有的列,除了第六列
#使用df.columns查看dataframe的列索引
[*df.columns] ![]()
#返回一个布尔值构成的数组,就只有索引为6的那一列为FALSE,其它列都是TRUE
df.columns !=6#新特征矩阵
#所有的行,然后对应的索引不是6的数据提取出来
df.iloc[:,df.columns !=6]#我们原始的标签是y_full
y_full#只有dataframe才能和dataframe拼接
#所以我们需要将上面的y_full转换成dataframe
y_full=pd.DataFrame(y_full)#将我们上面的原始的标签y_full和没有被选中去填充的特征矩阵拼接到一起
#第一个参数需要包含你想要连起来的所有的东西,然后用列表[]将其包括起来,axis=1,按照行进行匹配和连接
#也就是会将我们的y_full拼接在我们没有被选中去填充的特征矩阵的右边
df = pd.concat([df.iloc[:,df.columns != 6],pd.DataFrame(y_full)],axis=1)
df#在新特征矩阵中,对含有缺失值的列,进行0的填补
#实例化之后直接训练
#第一个参数missing_values传入的是缺失值是长什么样子的,也就是np.nan
#第二个参数是传入的模式是填充常数
#第三个参数是填充的值fill_value为0
#然后直接fit_transform,填补缺失值
df_0 =SimpleImputer(missing_values=np.nan,strategy='constant',fill_value=0).fit_transform(df)
df_0![]()
#验证有没有缺失值
pd.DataFrame(df_0).isnull().sum()④构建训练集和测试集
#找出我们的训练集和测试集
#Ytrain是被选中要填充的特征中(现在是我们的标签),存在的那些值,非空值
#也就是将我们为空值的那些数据全部都去除掉
Ytrain = fillc[fillc.notnull()]
Ytrain#是被选中的要填充的特征中(现在是我们的标签),不存在的那些值,是空值
#我们需要的不是Ytest本身,需要的是Ytest的索引
#我们需要知道在我们选出来要填充的特征中,那些为空,那些不为空
Ytest = fillc[fillc.isnull()]
Ytest#在新特征矩阵上,被选出来的要填充的特征的非空值所对应的记录
#也就是我们要根据Ytest中的索引将我们在新特征矩阵上对应的那些特征给取出来
#也就是我们的训练集
Xtrain = df_0[Ytrain.index,:]
Xtrain#新特征矩阵上,被选出来的要填充的那个特征的空值所对应的记录
Xtest = df_0[Ytest.index,:]
Xtest⑤用随机森林填补缺失值
#用随机森林回归来填补缺失值
#将随机森林进行实例化,其中生成的树为100棵
rfc = RandomForestRegressor(n_estimators=100)
#导入训练集去进行训练
rfc = rfc.fit(Xtrain, Ytrain)
#用predict接口将Xtest导入,得到我们的预测结果(回归结果),就是我们要用来填补空值的这些值
Ypredict = rfc.predict(Xtest)#返回了一串标签,这些标签都是我们用随机森林预测出来的
Ypredict#将填补好的特征返回到我们的原始的特征矩阵中
X_missing_regpd.DataFrame(df_0)X_missing_reg.iloc[:,6].isnull()#所引出初始的那个表的第六列中要填补缺失值的每一行
X_missing_reg.loc[X_missing_reg.iloc[:,6].isnull(),6]#将预测出来的结果赋给空值
X_missing_reg.loc[X_missing_reg.iloc[:,6].isnull(),6] = Ypredict#观察到索引为6的这一列全部没有空值了
X_missing_regX_missing_reg.isnull().sum()
#这样我们就完成了对于第六列的填补⑥循环填充
⑤仅仅是循环中的一次,这里我们还是需要循环填充缺失值
X_missing_reg = X_missing.copy()
sortindex = np.argsort(X_missing_reg.isnull().sum(axis=0)).values
#按照缺失值从少到多的顺序,全部遍历,也就是将上面的方法不断循环填补不同的列
for i in sortindex:
#构建我们的新特征矩阵和新标签
#更新df
df = X_missing_reg
fillc = df.iloc[:,i]
df = pd.concat([df.iloc[:,df.columns != i],pd.DataFrame(y_full)],axis=1)
#在新特征矩阵中,对含有缺失值的列,进行0的填补
#要填充0的列在越来越少
#填充出来之后都是在用回归出来的结果进行拟合
df_0 =SimpleImputer(missing_values=np.nan,
strategy='constant',fill_value=0).fit_transform(df)
#找出我们的训练集和测试集
Ytrain = fillc[fillc.notnull()]
Ytest = fillc[fillc.isnull()]
Xtrain = df_0[Ytrain.index,:]
Xtest = df_0[Ytest.index,:]
#用随机森林回归来填补缺失值
rfc = RandomForestRegressor(n_estimators=100)
rfc = rfc.fit(Xtrain, Ytrain)
Ypredict = rfc.predict(Xtest)
#将填补好的特征返回到我们的原始的特征矩阵中
X_missing_reg.loc[X_missing_reg.iloc[:,i].isnull(),i] = YpredictX_missing_reg#查看是否还有缺失值
X_missing_reg.isnull().sum()五、比较四种不同的预测效果
1.建模
#对填充好的数据进行建模
#对所有数据进行建模,取得MSE结果
#将这个列表命名为X,其中有四个特征
X = [X_full,X_missing_mean,X_missing_0,X_missing_reg]
mse = []
std = []
#让x在X中进行循环
for x in X:
#实例化回归森林
estimator = RandomForestRegressor(random_state=0, n_estimators=100)
#采用交叉验证的方式进行打分
#参数分别为评估器,标签,特征,打分的模式,交叉验证的次数
#将这五次的交叉打分的分数取平均值
scores = cross_val_score(estimator,x,y_full,scoring='neg_mean_squared_error',cv=5).mean()
mse.append(scores * -1)#mse越小越好
mse
#将不同的方法和其MSE的预测结果拼接起来
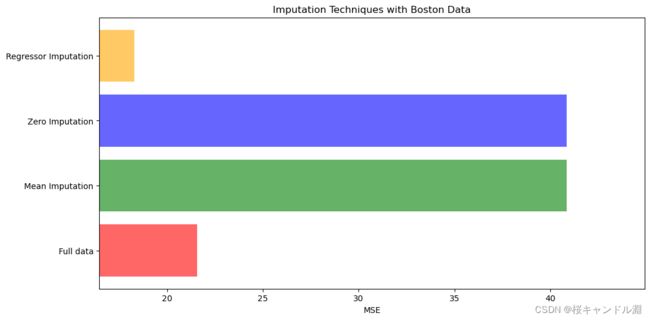
[*zip(["X_full","X_missing_mean","X_missing_0","X_missing_reg"],mse)]
#可以看出回归的成绩还是比较不错的2.绘图
#用所得的结果画出图形
#定义这四张图的名字
x_labels = ['Full data',
'Mean Imputation',
'Zero Imputation',
'Regressor Imputation']
#定义填充的颜色
colors = ['r', 'g', 'b', 'orange']
#画出画布
plt.figure(figsize=(12, 6))
#添加子图plt.subplot
#第一行,第一列,第一个表
ax = plt.subplot(111)
for i in np.arange(len(mse)):
#绘制一张条形图
#barh是bar horizontal的意思,就是将条形图横过来的意思
#第一个参数是0-3,取四个,也就是有四个数
#第二个参数就是我们mse中的分别对应的数据
#第三个参数,也就是传入每一条的颜色
#第四个参数,也就是传入每一条的粗细程度
#第五个参数align='center'也就是将条放在中心的位置上
ax.barh(i, mse[i],color=colors[i], alpha=0.6, align='center')
#填写标题:波士顿数据集在不同的填充标准下的表现
ax.set_title('Imputation Techniques with Boston Data')
#设置x轴的区间,最左边是mse的最小值取到0.9的地方,最右边是mse的最大值取到1.1倍的地方
#也就是说我们并不希望我们的横坐标从0刻度开始显示
ax.set_xlim(left=np.min(mse) * 0.9,right=np.max(mse) * 1.1)
#设置我们的y轴刻度
ax.set_yticks(np.arange(len(mse)))
#设置x轴的名称
ax.set_xlabel('MSE')
#请用x_labels中的这些东西作为y的命名
ax.set_yticklabels(x_labels)
#将图展示出来
plt.show()可以看出随机森林的预测效果还是非常不错的(mse分数越小越好!!)