视频超分算法EDVR：Video Restoration with Enhanced Deformable Convolutional Network超分辨率重建

这篇文章结合了TDAN中时间可变形网络的优势和Robust-VSR中融合注意力机制的优势，在此基础上注入了金字塔结构，提出了一种新的VSR方法EDVR（Enhanced Deformable Video Restoration），主要分为两个具体部分：金字塔级联可变形对齐网络（PCD) 和 时空注意力融合超分网络（TSA）。是适用于多种视频恢复任务的通用体系结构，包括超分辨率、去模糊、去噪、去块等。

原文链接：EDVR: Video Restoration with Enhanced Deformable Convolutional Networks[CVPR 2019]
参考目录：超分之EDVR
TDAN：Temporally-Deformable Alignment Network for Video Super-Resolution
DCN：Deformable Convolution Network
Robust-VSR：Robust Video Super-Resolution With Learned Temporal Dynamics

Abstract

EDVR整体结构上还是和往常的视频超分架构一样分为四部分：特征提取、对齐、融合和重建。只是深入研究了对齐和融合部分，使视频在包含大运动、遮挡和严重模糊时，仍能保持优异的性能。

2019年NTIRE视频超分挑战赛上发布了一个新的数据集，REalistic and Diverse Scenes dataset (REDS)。与现有数据集相比，REDS视频包含更大、更复杂的运动，使视频重建任务更真实、更具挑战性。之前的很多视频重建方法在该数据集上性能下降了很多。这也正推动了视频超分辨率重建任务的进步。

提出了金字塔级联可变形卷积对齐网络(PCD)和时空注意力融合SR网络(TSA)。

1. 金字塔级联可变形卷积对齐网络(PCD)，PCD基于可变形卷积DCN这种feature-wise、one-stage、flow-free的对齐方法，使用金字塔结构令DCN基于不同层级的feature map做对齐（不同层级代表不同频率的特征信息），并向更高分辨率的feature map层级传递和融合不同层级对齐后的feature map(offset)，产生一种从粗略到精确的隐式运动补偿结构。
2. 时空注意力融合SR网络(TSA)，TSA基于注意力机制，因不同帧和不同feature point包含的信息对图像重建的重要程度不同，通过分配不同的权重来关注重要信息，忽略无用或者错误的信息。在该网络中不仅使用了类似RCAN的空间注意力（SA），还使用了时间注意力（TA）。

1 Introduction

通常视频超分任务的pipeline由四个部分组成，即特征提取、对齐、融合和重建。当视频包含遮挡、大运动和严重模糊时，挑战在于对齐和融合模块的设计。为了获得高质量的输出，必须抓住两个关键：

1. 如何在多个帧之间对齐并建立精确的对应关系，大而复杂的运动很容易使得重建后的视频帧出现artifacts。
2. 如何有效地融合没法精确对齐的特征以进行重建。

而REDS数据集就是专门针对之前算法的上述缺陷而存在的。

大运动为什么会导致表现力下降？

1. 大运动导致对齐的难度增加。我们需要利用时间上的冗余信息来补充单帧的细节，前提是在前后图像对齐的情况下，否则两帧之间相差太多内容上完全不相关，肯定没法利用信息。大运动的存在导致运动轨迹很难捕捉，中间过程只能是随机推测，对齐的精确性肯定受到很大的影响，很可能会出现artifacts。对齐不准确在下个阶段融合的时候，会出现重叠或者模糊等等，影响SR的性能。
2. 在平滑、小幅度运动上也会因为对齐网络能力受限而影响融合SR网络表现力。原因：不管是基于Flow-based的对齐网络(如STN系列的VESPCN、Robust-LTD)还是基于Flow-free的对齐网络(如DCN系列的TDAN)都会存在一个粗略估计或者说无法做到精确对齐的问题。
3. 而flow-based对齐方法还有个严重的缺陷就是其严重依赖于运动估计的准确性，一旦估计出现问题就会使对齐出现artifacts，且后期很难修正。相对的基于DCN的flow-free对齐方法，是在特征级进行对齐，offset的粗略计算也可能会使得对齐的feature map出现artifacts，但feature-wise好在还有校正的空间，在后面接一层卷积可以减少artifacts的出现（TDAN中）。

如何进行有效融合来提升超分重建性能？
当对齐使得输入SR网络的对齐帧中出现了模糊、重影等artifacts或者当视频中存在多运动的情况下，在融合部分引入注意力机制，让网络更加关注能提高重建质量的特征信息，而忽略模糊、重影等特征信息，利用注意力机制来按重要性分配权重。

对近年来融合和对齐的发展进行简要回顾：
对齐：
  对齐主要分为2种方式：

1. 基于光流的方法（flow-based），使用STN作为基础，直接在Image-wise上对支持帧进行warp：典型的VSR结构有VESPCN、Robust-LTD等
2. 不依赖光流的方法（flow-free），使用DCN作为基础，在feature-wise上对支持帧的feature map进行对齐，隐式的运动补偿：典型的VSR结构有DUF、TDAN等。

问题：

1. 以往的方法都只是在单一分辨率尺度下进行对齐，所以不管是flow-based还是flow-free都无法在大运动视频中进行有效对齐。
2. 还有个对齐精确度的问题，上述的算法中除了VESPCN采用了2级的由粗到细的对齐之外，其余都只用了1级的对齐，故无法保证运动补偿的准确性。但VESPCN这种flow-based方法一来高度依赖于运动估计的准确性，二来其属于two-stage方法，故如果需要完成多级的对齐就需要花费更多的时间资源，相对flow-free这种one-stage方式来说更慢！

融合：

1. 在VESPCN中提出了Early fusion、Slow fusion、3D卷积三种融合方式；
2. Frame-Recurrent Video Super-Resolution和Recurrent Back-Projection Network for Video Super-Resolution采用循环神经网络进行特征融合；
3. Robust-LTD采用时间自适应网络来设计一个基于注意力机制来自动选择时间尺度的融合方式。

问题：

1. 不同的帧中包含不同程度重要性的信息，但是上述的这些融合方式对待不同的帧都是相同的方式，
2. 不同的feature point具有对于超分来说不同的价值，有的特征信息被不精确的对齐给弄模糊了或者出现重影等artifacts。

因此在EDVR中引入注意力机制，学习对特征中不同重要程度的信息分配不同的权重值。对那些不益于超分网络的训练的信息，分配微小的权重，而对有价值的信息分配较高的注意力权重。

针对以上问题，作者提出了EDVR方法，分别在对齐和融合两方面进行改进，提出了金字塔级联可变形卷积对齐网络(PCD)和时空注意力融合SR网络(TSA)。

对齐部分：
针对大运动问题，EDVR引出了金字塔级联可变形卷积对齐网络(PCD)，PCD基于可变形卷积DCN这种feature-wise、one-stage、flow-free的对齐方法，使用金字塔结构令DCN基于不同层级的feature map做对齐（不同层级代表不同频率的特征信息），并向更高分辨率的feature map层级传递和融合不同层级对齐后的feature map(offset)，产生一种从粗略到精确的隐式运动补偿结构；此外在金字塔外PCD额外设置一个TDAN来进一步提升对齐网络的鲁棒性。

融合部分：

针对多运动和模糊的融合，EDVR引出了时空注意力融合SR网络(TSA)，TSA基于注意力机制，因不同帧和不同feature point包含的信息对图像重建的重要程度不同，通过分配不同的权重来关注重要信息，忽略无用或者错误的信息。在该网络中不仅使用了类似RCAN的空间注意力（SA），还使用了时间注意力（TA）。时间注意力是计算支持帧与参考帧之间的相似度来获取权重，利用的是支持帧和参考帧之间的时间依赖。

---

2 Method

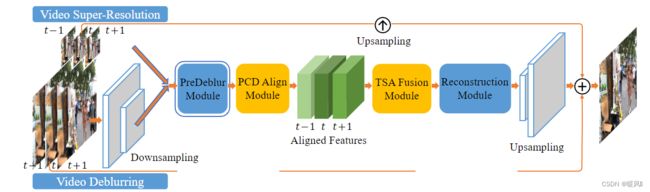
EDVR是个多功能视频重建网络，其包括超分、去模糊、去噪声、去块功能。
去模糊任务不在我们讨论的范围内，所以不详细讲。红色虚线圈住的灰色部分就是预模糊功能。

视频超分部分结构： 和其他VSR方法一样，输入是2N+1帧连续视频流$I_{[t-N:t+N]}^{LR}$，其中中间帧$I_t^{LR}$为参考帧。经过PCD对齐网络在特征级将每个相邻帧与参考帧对齐，得到对齐后的2N帧支持帧和一帧参考帧。再经过TSA融合模块融合不同帧的图像信息并提取特征后重建出SR’，重建模块是多个残差块的级联（可以用SR任务中其他高级模块替换），在网络的末端执行上采样操作以增大图像分辨率，再使用LR参考帧上采样后的图像作为正则化项进行修正，最后得到高分辨率SR。（去模糊模块对于超分也是有用的，它放在对齐模块之前可以有效减少输入端带来的模糊问题，从而提升对齐质量。）

对于具有高分辨率输入的其他任务（例如视频去模糊）：输入帧首先使用卷积下采样，使整个过程在低分辨率空间中进行计算（节省计算成本）。在对齐模块之前使用预模糊模块来预处理模糊输入并提高对齐精度。中间是超分的部分。最后的上采样层会将特征调整回原始输入分辨率。

note：作者使用了两份阶段策略，级联了两个EDVR网络，但第二个网络深度较浅，主要是为了细化第一阶段的输出帧。级联网络可以进一步消除先前模型无法处理的严重运动模糊。

---

2.1 Alignment with PCD

PCD（Pyramid, Cascading and Deformable Convolution）金字塔级联可变形卷积，是基于可变形卷积DCN（Deformable Convolution Net）的一种方法，类似于TDAN中包含时间信息的变体。但是TDAN中的对齐是比较粗糙的，只对齐了一次，而在PCD中作者引入了金字塔结构，分级逐步提取并融合特征，是一种由粗到细、feature-wise的方法。

先简单的了解下这个结构的概况：每次输入两帧图像$I_t$和$I_{t+i}$，第一步顺着倒金字塔的左边黄线方向做拼接和获取偏移量，第二步顺着紫线方向从最高层特征开始利用偏移做可变形卷积并往上一层合并（上采样，融合）。第三步是右上角浅紫色背景色的部分，将多层融合后的支持帧特征再和参考帧拼接单纯做一次TDAN，得到最终的对齐版特征图Aligned Features。

这一节需要用到TDAN的知识，实际上是一个加入时间信息的DCN的变体结构。

简单说一下为什么说是由粗到精的方法，这个粗略和精确针对的是位置特征的精确度。我们要做的工作是对齐，对齐最重要的是位置信息。在金字塔底层，图像特征分辨率最高（图像大小最大），位置信息更加精确。黄线部分的特征提取只是可变形卷积的一个预处理工作。PCD先对分辨率最小的feature map 进行可变形卷积进行粗略的对齐，然后将offset和feature map向更高分辨率的特征图像传递，每次对齐都将变得更加精确。

PCD对齐模块基于DCN(可变形卷积)，它和TDAN中对于DCN的用法几乎完全一样，唯一不同的是，TDAN中只用了一个DCN网络；而PCD使用了多个DCN网络和卷积网络进行级联形成金字塔结构，并且每个DCN都是基于不同层级的feature map进行对齐，故PCD的对齐是一种从粗到细、自顶向下的过程。

首先介绍一下PCD中可变形卷积是怎么做的：
不同于经典的DCN，VSR中的DCN由于需要结合时间信息，输入为两帧图像，因此需要先将参考帧和支持帧简单融合，一般是使用Early fusion进行直接concat后接一个卷积层减少通道维度。再通过一个卷积层学习得到offset，使用算子$f(\cdot )$表示学习offset的网络。$F_{t+i},i\in [-N,N]$表示$2N+1$帧图像(每个样本包含2N+1帧图像)，其中$F_t$为参考帧，其余为支持帧，则偏移矩阵$\Delta P$表达式为：
$$\Delta P_{t+i}=f([F_{t+i},F_t]),i\in \{-N,\cdots ,1,\cdots ,N\}.\text{\hspace{1em}(1)}$$
其中$\Delta P=\{\Delta p\}$，$[\cdot ,\cdot ]$ 表示concat操作。

$\Delta P_{t+i}$的分辨率和$F_{t+i}$是一样的（得到的是整个patch中每个位置的偏移量），深度为2K或者K均可（2K表示x、y两个方向）。
有了offset，接下来将offset用于支持帧$F_{t+i},i\in \{-N,\cdots ,-1,1,\cdots ,N\}$，得到位置变换后的特征图像，一般得到的新位置都是亚像素坐标，故会通过双线性插值去获取对应像素值，并对位置变换之后的支持帧进行卷积，输出对齐之后的支持特征图$F_{t+i}^a$，具体表达式为：
$$F_{t+i}^a=\sum _{k=1}^{K}w(p_k)\cdot F_{t+i}(\underset{p}{p_0+p_k+\Delta p_k})+b(p_k),\text{\hspace{1em}(2)}$$

其中$w(p_k)、b(p_k)$表示可变形卷积的参数，$p_k$表示卷积核中的某一个位置，假设3 × 3卷积，则$p_k\in \{(-1,-1),(-1,0),\cdots ,(1,1)\}$且K表示一个卷积核的参数个数。

接下来介绍金字塔级联结构是怎么样的：(PCD整体过程）

第一步：（黄色指向线①）
首先将同一时间窗口下的2帧图像(参考帧和支持帧)通过卷积输出各自的feature map，作为第一层的特征信息$F_{t+i}^1$；接着使用跨步卷积产生下采样为2的特征信息$F_{t+i}^l$ ，其中某一层$l\in [1,L]$，上图中$L=3$，即产生了3个层级的特征信息，每层的分辨率依次以$\times 2$进行衰减。
第二步：（紫色线②）
从顶层$L3$开始，对该层参考帧和支持帧的特征进行融合(concat+卷积减少维度)，通过卷积求得该层的offset，利用offset和该层的支持feature map输出该层对齐之后的参考特征图$(F_{t+i}^a{)}^3$(上标中的“3”表示金字塔的第3层)。

接着将第3层学习到的offset和该层对齐之后的参考特征图$(F_{t+i}^a{)}^3$输送给下一层，即第二层。第二层的offset由该层的两个feature map 经过融合求得的offset再和上一层得到的offset上采样后共同组。该层输出的对齐feature map不仅来源于该层可变形卷积的输出，还取决于上一层的对齐feature map（和offset类似的操作）。具体表达式为：
$$\Delta P_{t+i}^l=h([f([F_{t+i},F_t]),(\Delta P_{t+i}^{l+1}{)}^{\uparrow 2}]),\text{\hspace{1em}(3)}$$
$$(F_{t+i}^a{)}^l=g([DConv(F_{t+i},\Delta P_{t+i}^l),((F_{t+i}^a{)}^{l+1}{)}^{\uparrow 2}]).\text{\hspace{1em}(4)}$$
其中$(\cdot {)}^{\uparrow 2}$表示使用双线性插值进行2倍上采样；$DCon(\cdot )$表示可变形卷积；$g(\cdot ),h(\cdot )$表示一般的卷积过程；$[\cdot ,\cdot ]$表示concat。

一直传递向分辨率高的层传递直到最后一层，第1层（也就是金字塔的底层），得到对齐的支持帧feature map。

第三步：（浅紫色背景框③）
在金字塔结构之外，单纯做一个TDAN。将第1层的参考帧feature map和得到的对齐支持帧feature map$(F_{t+i}^a{)}^1$进行融合得到一个offset，然后利用这个offset和$(F_{t+i}^a{)}^1$进行可变形卷积输出最终对齐的支持特征图。这样可以进一步调整校正对齐feature map。提高网络的鲁棒性。

PCD金字塔结构的优点：

1. 使用DCN作为基础块，相比于二阶段的STN，DCN是one-stage的，速度上更加有优势。再者DCN基于feature-wise，是一种隐式运动补偿，能减少artifacts的影响，并且不依赖于光流估计的精确度。
2. 多个DCN级联，且每个DCN基于不同层级的feature map，针对不同分辨率的特征，由粗到细的进行运动补偿来完成支持帧和参考帧特征的对齐，多级的DCN结构有助于提升对齐的准确性。基于不同的特征图进行可变形卷积能产生更多复杂的变换，从而让PCD对齐学习到大运动或者复杂运动下如何对齐支持帧到参考帧。

---

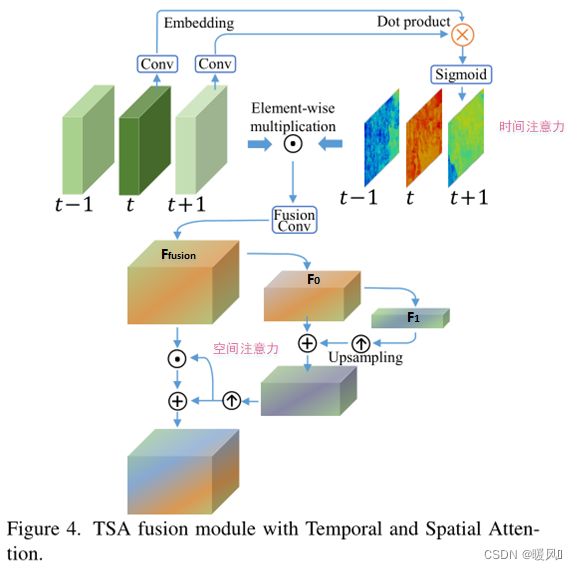
2.2 Fusion with TSA

充分利用帧间的时间关系和帧内的空间关系在融合中至关重要，但

1. 不同的相邻帧包含信息的重要程度不同，因为一些atrifacts的存在（重影、模糊、遮挡等）
2. 前一阶段的对齐如果出现精度较低或者对齐不准的问题，会导致融合的时候前后帧内容不一致，影响重建的效果。

为了解决上述问题，在时间和空间上引入注意力机制，忽略不好的特征信息，关注重要的特征信息。提出了TSA融合模块来为每一帧分配像素级的聚合权重，提高融合的有效性和高效性。

概述：

1. 时间注意力：输入为2N+1帧，先卷积再求出每帧和参考帧之间的相似度：通过和参考帧点乘再经过Sigmoid（参考帧和自己做点乘）得到每帧的时间注意力权重（像素级）。再与2N+1帧输入做元素乘法、卷积，得到时间融合后的结果$F_{fusion}$。
2. 空间注意力：时间融合后的特征$F_{fusion}$经过两次卷积下采样，经过一次{上采样和上一层特征相加}，再一次上采样获得空间注意力权重值（size和$F_{fusion}$相同）。获得的注意力权重加上本身和$F_{fusion}$元素相乘后的值得到最终的支持帧估计值。

时间注意力:
时间注意力的目标是计算不同帧与参考帧之间的相似度，也就是说与参考帧相似的相邻帧的重要性高，应该分配更多的权重（特征元素级）。

时间注意力网络的设计是先进行卷积，再求出每帧和参考帧之间的相似度，然后通过element-wise将输入和注意力权重相结合。用$\theta (\cdot )、\varphi (\cdot )$分别表示对支持feature map和参考feature map的卷积，故求时间注意力权值的公式为：
$$h(F_{t+i}^a,F_t^a)=sigmoid(\theta (F_{t+i}^a{)}^T\varphi (F_t^a)).\text{\hspace{1em}(5)}$$
$sigmoid(\cdot )$在注意力设计中是结合门机制来将权重缩进在0~1之间，有助于增加训练的稳定性。在RCAN中通道注意力CA可以看成是residual scaling的一种方式。

获取注意力权值之后，就可以进行时间融合输出$F_{fusion}$，公式如下：
$${\tilde{F}}_{t+i}^a=F_{t+i}^a\odot h(F_{t+i}^a,F_t^a),\text{\hspace{1em}(6)}$$
$$F_{fusion}=Conv([{\tilde{F}}_{t-N}^a,\cdots ,{\tilde{F}}_t^a,\cdots ,{\tilde{F}}_{t+N}^a]).\text{\hspace{1em}(7)}$$

其中$[\cdot ,\cdot ]$表示concat，式(7)本质就是个Early fusion。

空间注意力:
通过时间融合后的结果可以看成是个不含时间维度的feature map。
时间融合后输出$F_{fusion}$先使用2次卷积下采样，然后通过上采样、相加等操作获取和$F_{fusion}$相同size的空间注意力，最后通过element-wise的相乘来输出结合空间注意力融合的feature map，最后传送进重建网络输出高分辨率版本的支持帧。空间注意力的具体表达式如下：
$$\begin{gathered} F_0=Conv(F_{fusion}), \\ {F}_1=Conv(F_0), \\ {F}_2=F_0+F_1^{\uparrow }, \\ F=F_2^{\uparrow }+F_{fusion}\odot F_2^{\uparrow }. \end{gathered}$$
其中$(\cdot {)}^{\uparrow }、\odot$分别表示上采样和element-wise相乘。

---

两阶段策略：
级联了两个EDVR网络，但第二个网络深度较浅，主要是为了细化第一阶段的输出帧。级联网络可以进一步消除先前模型无法处理的严重运动模糊。

1. 有效地消除了单一EDVR块无法处理的模糊问题，提高了恢复质量；
2. 缓解了单一EDVR块输出帧之间的不连续性。

3 Experiments

训练：
REDS数据集，这个数据集分辨率为720p，训练集一共240个视频，测试集和验证集各有30个视频，但是测试集不公开，所以作者抽取了4个视频作为测试集(REDS4)，其余的266个视频作为训练和验证来用。
Vimeo-90K训练数据集。这个数据集分辨率较低，但是数量多。

测试：
在Vid4和Vimeo-90K-T上测试。Vid4中的4个视频相对运动较慢；Vimeo-90K-T相对较大，有很多运动和场景；REDS4是一个高清且有更大更复杂的运动视频。

setting：
PCD中特征提取阶段使用5个残差块提取特征。
$(EDVR{)}_1$ 中的SR重建部分使用40个残差块；$(EDVR{)}_2$中的SR重建部分使用20个残差块。残差块的通道都设置为128。
超分训练patch为64 × 64，对于去模糊任务的patch256×256。
batch=32。
1个样本包含连续5帧。
训练时候采用水平翻转和旋转90°两种自增强。
训练损失函数为$\mathcal{L}=\sqrt{||{\hat{O}}_t-O_t|{|}^2+{ϵ}^2},ϵ=10^{-3}$
Adam优化，初始学习率设置为$4\times 10^{-4}$
先训练浅层的$(EDVR{)}_2$，然后将它的参数作为深层$(EDVR{)}_1$的初始化参数来加快收敛。

实验对比了不同SOTA方法之间的结果；研究了PCD和TSA各自的作用和效果;研究了数据集偏差；
具体实验对比参看超分之EDVR

结论：

1. 在Vid4这种慢性运动视频上，EDVR和DUF取得了最佳的重建性能，但是EDVR没有拉开差距。
2. 在REDS4测试上，EDVR展示了其适应于大而复杂运动下的超分能力，和DUF拉开了差距。
3. PCD可以对齐较大运动下的支持帧和参考帧，TSA模块会给对齐的越好的帧分配越高的权值，提高重建性能。
4. 在不同数据集上训练在相同测试集上结果会有较大的偏差。
5. 自集成对于VSR性能提升效果很小，而two-stage策略对于性能提升较大。

4 Conclutions

这篇文章主要针对VSR任务中的对齐部分和融合部分进行了改进，汲取了TDAN中时间可变形网络和Robust-VSR中融合注意力机制的优点，用金字塔结构作为框架。主要分为两个具体部分：金字塔级联可变形对齐网络（PCD) 和 时空注意力融合超分网络（TSA）。

1. PCD中多个DCN级联，且每个DCN基于不同层级的feature map，由粗到细的进行运动补偿来完成支持帧和参考帧特征的对齐，多级的DCN结构有助于提升对齐的准确性。基于不同的特征图进行可变形卷积能产生更多复杂的变换，从而让PCD对齐学习到大运动或者复杂运动下如何对齐支持帧到参考帧。
2. TSA中利用了时间和空间注意力，与参考帧更相似的相邻帧会分配更高的权重值，对于在对齐模块没有精确对齐的帧或者位置都会分配较小的权重值。（element-wise）
3. 新的视频数据集REDS包含更大、更复杂的运动，使视频重建任务更真实、更具挑战性，而EDVR能够轻松的应对。
4. EDVR是适用于多种视频恢复任务的通用体系结构，包括超分辨率、去模糊、去噪、去块等

---

记录一个背景色用法：
$超分算法EDVR$

	$\colorbox{blue}{超分算法EDVR}$            ##蓝底白字

---

最后祝各位科研顺利，身体健康，万事胜意~