机器学习笔记-数据预处理（标准化、归一化）（未完）

机器学习笔记-数据预处理（标准化、归一化）

数据预处理（使用Scikit-Learn）

sklearn.preprocessing 包

sklearn.preprocessing 包提供了几个常用的效用函数和变换类，可以将原始特征向量转化为更适合其后的估计函数所需的形式。

也就是对数据进行标准化处理。比如说，假如集合中存在异常值，使用robust scalers或者transformers就更合适一些。

数据标准化Z-score（0-1标准化：移除平均值，将方差化为1）

经过这种方法处理的数据符合标准正态分布，即均值为0，标准差为1。标准化并不会改变数据的分布。之所以会说标准化之后数据变成标准正态分布，是因为原始的数据就是符合正态分布的，只不过并不是标准正态分布。

标准化是对特征（feature）进行操作的，也就是对列进行操作。对于同一列的所有特征我们对其进行标准化处理就是对该列执行以下操作：
$$X=(X-\mu )/\delta$$
其中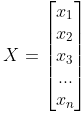为某一列feature，μ是平均值mean(X)，而δ是X的均方差（也叫标准差 )std(X)。

P.S.均方差：
$$\sum (x-xi{)}^2/n$$
*对于个别特征，以及不同于标准正态分布数据（均值为0和单位化方差的高斯分布）的数据表现不好。

用法示例：

>>> from sklearn import preprocessing
>>> import numpy as np
>>> X_train = np.array([[ 1., -1.,  2.], # 训练数据集
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
>>> scaler = preprocessing.StandardScaler().fit(X_train) # 创建用于标准化的scaler对象
>>> scaler
StandardScaler()

>>> scaler.mean_ # 每一列的均值
array([1. ..., 0. ..., 0.33...]) 

>>> scaler.scale_ # 缩放比例
array([0.81..., 0.81..., 1.24...])

>>> X_scaled = scaler.transform(X_train) # 得到标准化后的矩阵
>>> X_scaled
array([[ 0.  ..., -1.22...,  1.33...],
       [ 1.22...,  0.  ..., -0.26...],
       [-1.22...,  1.22..., -1.06...]])

# 也可以直接fit后用接口导出
>>> scaler = StandardScaler()
>>> X_scaled = scaler.fit_transform(X_train)

数据归一化

可以将数据按最小值中心化后，再按极差（最大值-最小值）缩放，收敛到一个给定的最大值和最小值区间，一般为0到1之间；或者将最大值的绝对值限定为单位制。使用MinMaxScaler或者MaxAbsScaler来分别实现。

用法示例：

>>> X_train = np.array([[ 1., -1.,  2.],
...                     [ 2.,  0.,  0.],
...                     [ 0.,  1., -1.]])
...
>>> min_max_scaler = preprocessing.MinMaxScaler()
# fit，在这里本质是生成min(x)和max(x)，再通过transform接口导出结果。
>>> X_train_minmax = min_max_scaler.fit_transform(X_train) 
>>> X_train_minmax
array([[0.5       , 0.        , 1.        ],
       [1.        , 0.5       , 0.33333333],
       [0.        , 1.        , 0.        ]])

如果MinMaxScaler被显式设置了最大最小值，公式是：

X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

X_scaled = X_std * (max - min) + min

归一化 Normalization/Min-Max Scaler会严格的限定数据变化后的范围，默认的是将数据控制在 [0,1] 之间。而标准化 Standardization 之后的数据没有严格的区间，变化之后的数据没有范围，只是数据整体的均值为0，标准差为1。

另外，归一化缩放的比例仅仅和极值有关，而标准化缩放的比例和整体数据集有关。所以对于存在异常数据的样本来说，用归一化并不是一个聪明的决定。

直接使用numpy来进行预处理

归一化：

# 归一化
X_nor = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))

# 逆转归一化
X_returned = X_nor * (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)
0) - X.min(axis=0))

# 逆转归一化
X_returned = X_nor * (X.max(axis=0) - X.min(axis=0)) + X.min(axis=0)