【PyTorch】深度学习实践之CNN高级篇——实现复杂网络
本文目录
- 1. 串行的网络结构
- 2. GoogLeNet
- 2.1 结构分析
- 2.2 代码实现
- 2.3 结果
- 3. ResNet
- 3.1 网络分析
- 3.2 代码实现
- 3.3 结果
- 课后练习1:阅读并实现Identity Mappings in Deep Residual Networks
- 实现图左的Residual Block:
- 实现图右的Residual Block:
- 课后练习2:阅读和实现 Densely Connected Convolutional Networks(DenseNet)
- 代码
- 结果:
- 学习资料
- 系列文章索引
1. 串行的网络结构
之前的网络结构,不管是全连接神经网络还是卷积神经网络,都是一种串行的结构。
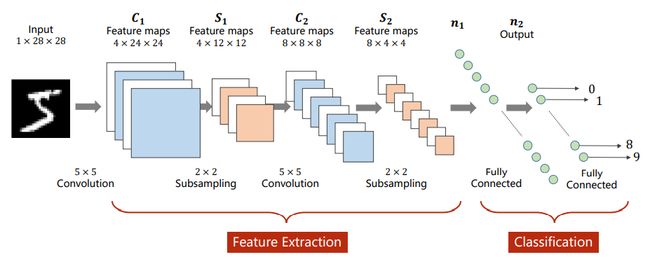
2. GoogLeNet
2.1 结构分析
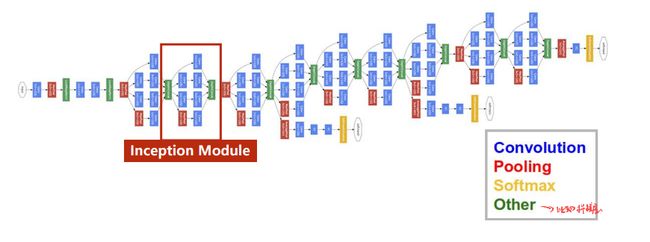
如上图所示,网络结构其实有很多重复的地方,因此为了减少代码冗余,会使用函数/类。
GooleNet的网络结构,里面的模块称为inception,如下所示:
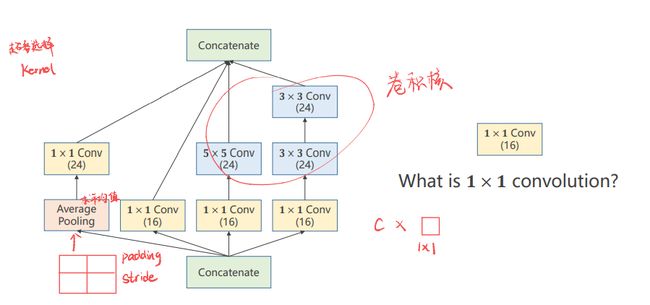
inception模块 的构成方式其实有很多种,这只是其中的一种。首先需要知道inception为什么这样构建?
因为构建的时候有一些超参数是比较难选的,比如卷积核的大小,是使用3x3,还是5x5还是使用其他的方式。
GooleNet的出发点就是不知道哪个卷积核好用,那么就在一个块里面把卷积核都使用一下,然后把他们结果挪到一起,之后如果3x3的好用,自然3x3的权重就会变得比较大,其他路线的权重相对就会变得更小,所以这是提供了几种后续的神经网络的配置,然后通过训练自动的找到最优的卷积的组合。
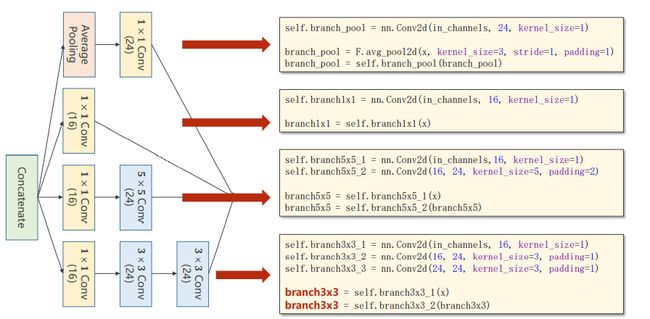
Concatenate: 把张量拼接到一块。4条路径算出来4个张量,所以肯定要做一个拼接。
Average Pooling: 均值池化,4条分支后续要进行拼接,所以必须要保持他们的宽度和高度是一致的,输出的图像格式为(B,C,W,H),唯一可以不同的就是C(channel),不同的卷积核为了使得输出的W和H一致,可以通过padding来实现。
之前使用的是2x2的最大池化,导致图像变成了原来的一半,所以解决方案是做池化的时候认为的指定stride=1,padding= 多少。例如使用3x3的大小去做均值,可以使用padding=1,有点类似卷积的操作,但是没有卷积核,使用的可以称为均值卷积核,卷积核中的数都一样,所以均值池化可以通过设置stride和padding使得输入输出图像的大小是一致的。
1x1的卷积: 代表卷积核大小就是1x1的,1x1卷积的个数取决于输出张量的通道数。

- 1x1的卷积完成了一个信息融合,其主要工作就是改变通道数,减小复杂度。
- 神经网络里面的问题就是运算量太大,所以我们需要思考怎么解决运算量大的问题。在原来的基础上添加了一层1x1的卷积层之后,运算量变为了原来的1/10。

ps:上图最后一行少了branch = self.branch3x3_3(branch3x3)
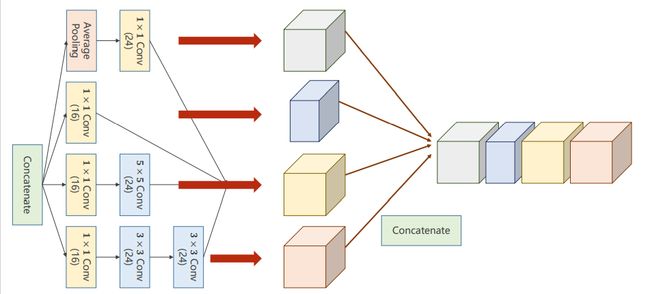
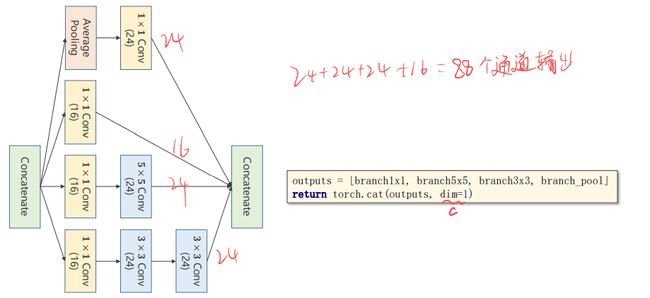
在各个计算完成之后还需要拼接,按照各个通道进行拼接,如图所示:
2.2 代码实现
# inception模块
class Inception(nn.Module):
def __init__(self,in_channels):
super(Inception, self).__init__()
self.branch1x1 = nn.Conv2d(in_channels,16,kernel_size=1)
self.branch5x1 = nn.Conv2d(in_channels,16,kernel_size=1)
self.branch5x2 = nn.Conv2d(16,24,kernel_size=5,padding=2)
self.branch3x1 = nn.Conv2d(in_channels,16,kernel_size=1)
self.branch3x2 = nn.Conv2d(16,24,kernel_size=3,padding=1)
self.branch3x3 = nn.Conv2d(24,24,kernel_size=3,padding=1)
self.branch_pool = nn.Conv2d(in_channels,24,kernel_size=1)
def forward(self,x):
branch1x1 = self.branch1x1(x)
branch5x5 = self.branch5x1(x)
branch5x5 = self.branch5x2(branch5x5)
branch3x3 = self.branch3x1(x)
branch3x3 = self.branch3x2(branch3x3)
branch3x3 = self.branch3x3(branch3x3)
branch_pool = f.avg_pool2d(x,kernel_size = 3,stride = 1,padding = 1)
branch_pool = self.branch_pool(branch_pool)
outputs = [branch1x1,branch5x5,branch3x3,branch_pool]
return torch.cat(outputs,dim=1) # 按通道进行拼接
注意:初始的输入通道没有写死,而是作为in_channels入参设置。
# 网络模块
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.conv1 = nn.Conv2d(1,10,kernel_size=5)
self.conv2 = nn.Conv2d(88,20,kernel_size=5)
self.incep1 = Inception(in_channels=10)
self.incep2 = Inception(in_channels=20)
self.mp = nn.MaxPool2d(2)
self.fc = nn.Linear(1408,10)
def forward(self,x):
in_size = x.size(0)
x = f.relu(self.mp(self.conv1(x))) # 10通道
x = self.incep1(x) # 10通道变88通道
x = f.relu(self.mp(self.conv2(x))) # 88通道变20通道
x = self.incep2(x) # 20通道变88通道
x = x.view(in_size,-1) # 这里可以计算出拉成一维以后的大小
x = self.fc(x)
return x
2.3 结果
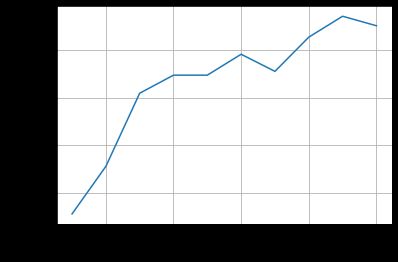
使用MNIST数据集测试Inception网络模型,结果如下:
性能略微提升,说明改变卷积层的结构还是有效果。此外,观察结果图可以发现,准确率上升到最高点后出现了下降。
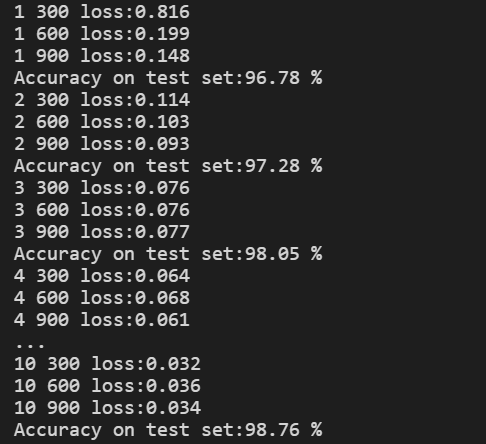
注意:一般我们在训练的过程中,我们会保存我们每个epoch训练的结果,最后我们会在测试集上选用准确率高的训练模型。我们需要注意的是不是说训练的次数越多,网络的性能越好,训练的多了可能出现过拟合,导致模型的泛化能力变差。
3. ResNet
3.1 网络分析
叠加卷积层,效果会更好吗?把3x3的网络一直堆下去,实验发现层数越多,反而错误率越高。
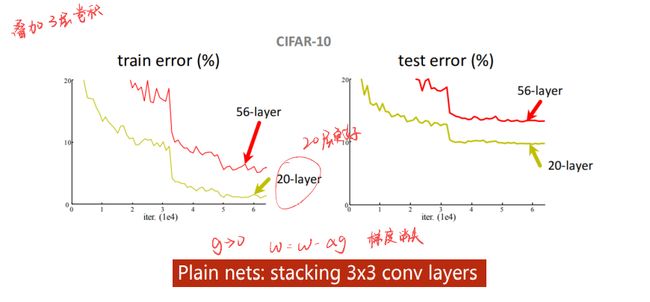
思考可能是梯度消失,因为我们的网络会进行反向传播,而反向传播的本质是链式法则。假如一连串的梯度是小于1的,这样乘起来就会越来越小,最终趋近于0。
而我们的权重更新是:w = w - 学习率*梯度,如果梯度接近0了,那么他们的权重w就基本得不到什么更新。
解决梯度消失的思路:
假如有一个512的隐藏层,然后后面直接接一个512x10的层进行训练,训练完成以后,把512层进行冻结;
然后再添加一个256的层,后面接256x10进行训练,训练完成以后,还是对256层进行加锁,逐层的进行训练。
通过以上这种训练方式来解决梯度消失的问题。但是在深度学习里面,这样做的话其实是一件很困难的事情,因为深度学习的层数是非常多的。
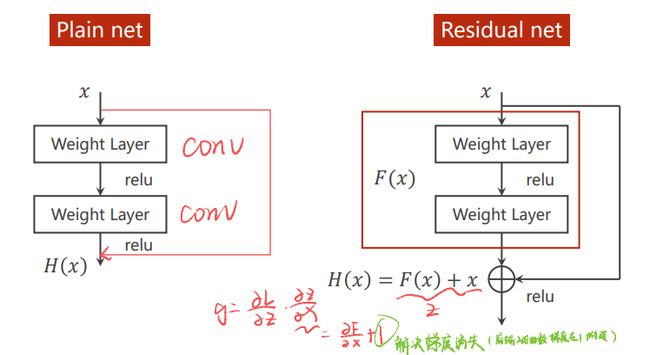
ResNet引入残差结构以解决网路层数加深时导致的梯度消失问题。 通过短路连接,可以实现在计算梯度的时候不至于接近0,而是梯度小的时候,计算的梯度值在1附近,这就是Resnet网络的智慧所在。
3.2 代码实现
# ResidualBlock模块
class ResidualBlock(nn.Module):
def __init__(self,channels):
super(ResidualBlock, self).__init__()
self.channels = channels
self.conv1 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
self.conv2 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
def forward(self,x):
y = f.relu(self.conv1(x))
y = self.conv2(y)
return f.relu(x+y)
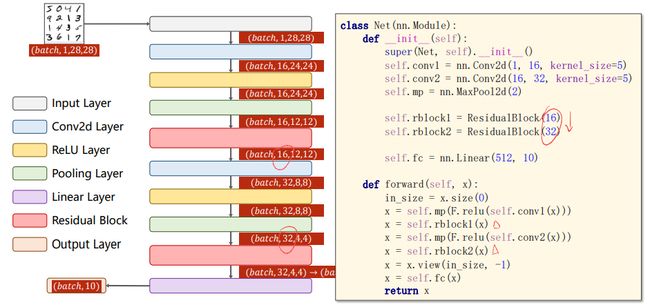
# 网络模块
class Model(nn.Module):
def __init__(self):
super(Model, self).__init__()
self.conv1 = nn.Conv2d(1,16,kernel_size=5)
self.conv2 = nn.Conv2d(16,32,kernel_size=5)
self.mp = nn.MaxPool2d(2)
self.rblock1 = ResidualBlock(16)
self.rblock2 = ResidualBlock(32)
self.fc = nn.Linear(512,10)
def forward(self,x):
in_size = x.size(0)
x = self.mp(f.relu(self.conv1(x)))
x = self.rblock1(x)
x = self.mp(f.relu(self.conv2(x)))
x = self.rblock2(x)
x = x.view(in_size,-1)
x = self.fc(x)
return x
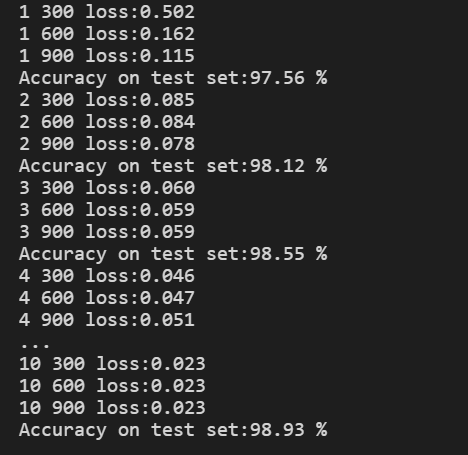
3.3 结果
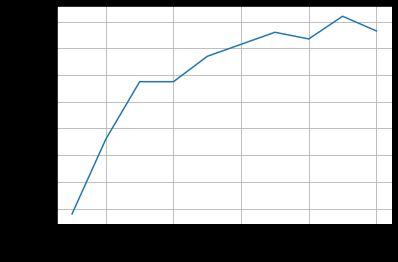
依然是在MNIST数据集上测试,结果如下:
比GoogleNet准确率更高,到了99%
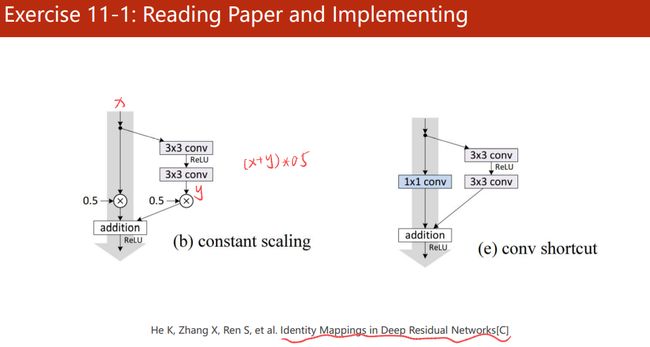
课后练习1:阅读并实现Identity Mappings in Deep Residual Networks
实现图左的Residual Block:
class ResidualBlock(nn.Module):
def __init__(self,channels):
super(ResidualBlock,self).__init__()
self.channels = channels #实现异步
self.conv1 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
self.conv2 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
def forward(self,x):
y = f.relu(self.conv1(x))
y = self.conv2(y)
return f.relu((x+y)*0.5)
实现图右的Residual Block:
class ResidualBlock(nn.Module):
def __init__(self,channels):
super(ResidualBlock,self).__init__()
self.channels = channels #实现异步
self.conv1 = nn.Conv2d(channels,channels,kernel_size=3,padding=1) #padding=1 保证图像输入输出前后的尺寸大小不变
self.conv2 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
self.conv11 = nn.Conv2d(channels,channels,kernel_size=1) #实现1x1卷积
def forward(self,x):
y = f.relu(self.conv1(x))
y = self.conv2(y)
x = self.conv11(x)
return f.relu(x+y)
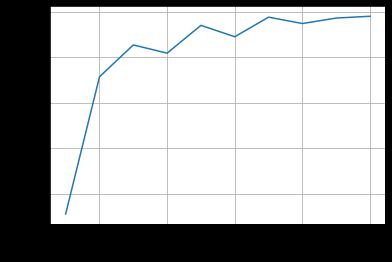
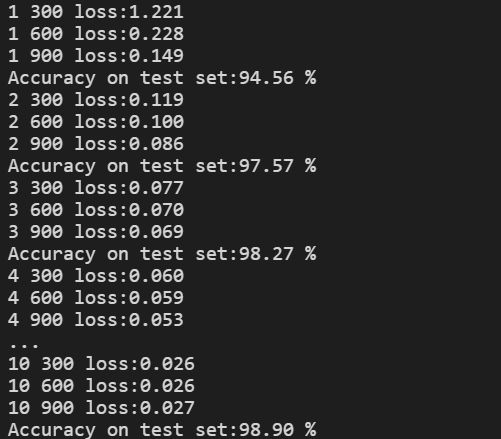
结果:
比左图ResidualBlock准确率更好,但是震荡比较多。
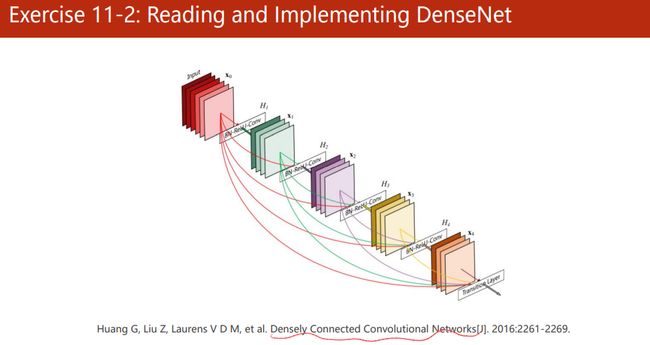
课后练习2:阅读和实现 Densely Connected Convolutional Networks(DenseNet)
https://www.codeleading.com/article/89321102194/
代码
from __future__ import print_function
import torch
import time
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
from torch import optim
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision.transforms import ToPILImage
show=ToPILImage()
import numpy as np
import matplotlib.pyplot as plt
batchSize=32
##load data
# transform = transforms.Compose([transforms.Resize(96),transforms.ToTensor(),transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# transform = transforms.Compose([transforms.Resize(96),transforms.ToTensor(),transforms.Lambda(lambda x: x.repeat(3,1,1)),transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
transform = transforms.Compose([
transforms.Resize(96),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=False, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batchSize, shuffle=True, num_workers=0)
testset = torchvision.datasets.MNIST(root='./data', train=False, download=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=batchSize, shuffle=False, num_workers=0)
def imshow(img):
img = img / 2 + 0.5
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
####network
class conv_blk(nn.Module):
def __init__(self,in_channel,num_channel):
super(conv_blk, self).__init__()
self.blk=nn.Sequential(nn.BatchNorm2d(in_channel,eps=1e-3),
nn.ReLU(),
nn.Conv2d(in_channels=in_channel,out_channels=num_channel,kernel_size=3,padding=1))
def forward(self, x):
return self.blk(x)
class DenseBlock(nn.Module):
def __init__(self,in_channel,num_convs,num_channels):
super(DenseBlock,self).__init__()
layers=[]
for i in range(num_convs):
layers+=[conv_blk(in_channel,num_channels)]
in_channel=in_channel+num_channels
self.net=nn.Sequential(*layers)
def forward(self,x):
for blk in self.net:
y=blk(x)
x=torch.cat((x,y),dim=1)
return x
def transition_blk(in_channel,num_channels):
blk=nn.Sequential(nn.BatchNorm2d(in_channel,eps=1e-3),
nn.ReLU(),
nn.Conv2d(in_channels=in_channel,out_channels=num_channels,kernel_size=1),
nn.AvgPool2d(kernel_size=2,stride=2))
return blk
class DenseNet(nn.Module):
def __init__(self,in_channel,num_classes):
super(DenseNet,self).__init__()
self.block1=nn.Sequential(nn.Conv2d(in_channels=in_channel,out_channels=64,kernel_size=7,stride=2,padding=3),
nn.BatchNorm2d(64,eps=1e-3),
nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2,padding=1))
num_channels, growth_rate = 64, 32 # num_channels:当前的通道数。
num_convs_in_dense_blocks = [4, 4, 4, 4]
layers=[]
for i ,num_convs in enumerate(num_convs_in_dense_blocks):
layers+=[DenseBlock(num_channels,num_convs,growth_rate)]
num_channels+=num_convs*growth_rate
if i!=len(num_convs_in_dense_blocks)-1:
layers+=[transition_blk(num_channels,num_channels//2)]
num_channels=num_channels//2
layers+=[nn.BatchNorm2d(num_channels),nn.ReLU(),nn.AvgPool2d(kernel_size=3)]
self.block2=nn.Sequential(*layers)
self.dense=nn.Linear(248,10)
def forward(self,x):
y=self.block1(x)
y=self.block2(y)
y=y.view(-1,248)
y=self.dense(y)
return y
net=DenseNet(1,10).cuda()
print (net)
criterion=nn.CrossEntropyLoss()
optimizer=optim.SGD(net.parameters(),lr=0.1,momentum=0.9)
#train
print ("training begin")
for epoch in range(1):
start = time.time()
running_loss=0
for i,data in enumerate(trainloader,0):
# print (inputs,labels)
image,label=data
image=image.cuda()
label=label.cuda()
image=Variable(image)
label=Variable(label)
# imshow(torchvision.utils.make_grid(image))
# plt.show()
# print (label)
optimizer.zero_grad()
outputs=net(image)
# print (outputs)
loss=criterion(outputs,label)
loss.backward()
optimizer.step()
running_loss+=loss.data
if i%100==99:
end=time.time()
print ('[epoch %d,imgs %5d] loss: %.7f time: %0.3f s'%(epoch+1,(i+1)*batchSize,running_loss/100,(end-start)))
start=time.time()
running_loss=0
print ("finish training")
#test
net.eval()
correct=0
total=0
for data in testloader:
images,labels=data
images=images.cuda()
labels=labels.cuda()
outputs=net(Variable(images))
_,predicted=torch.max(outputs,1)
total+=labels.size(0)
correct+=(predicted==labels).sum()
print('Accuracy of the network on the %d test images: %d %%' % (total , 100 * correct / total))
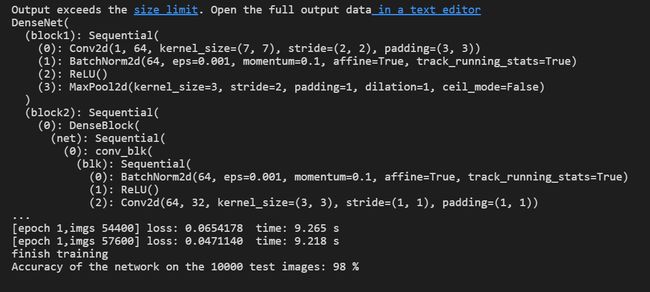
结果:
学习资料
- https://blog.csdn.net/lizhuangabby/article/details/125837409
系列文章索引
教程指路:【《PyTorch深度学习实践》完结合集】 https://www.bilibili.com/video/BV1Y7411d7Ys?share_source=copy_web&vd_source=3d4224b4fa4af57813fe954f52f8fbe7
- 线性模型 Linear Model
- 梯度下降 Gradient Descent
- 反向传播 Back Propagation
- 用PyTorch实现线性回归 Linear Regression with Pytorch
- 逻辑斯蒂回归 Logistic Regression
- 多维度输入 Multiple Dimension Input
- 加载数据集Dataset and Dataloader
- 用Softmax和CrossEntroyLoss解决多分类问题(Minst数据集)
- CNN基础篇——卷积神经网络跑Minst数据集
- CNN高级篇——实现复杂网络
- RNN基础篇——实现RNN
- RNN高级篇—实现分类