【Matlab 六自由度机器人】定义标准型及改进型D-H参数建立机器人模型（附MATLAB建模代码）

近期更新

【汇总】

$\boxed{【Matlab六自由度机器人】系列文章汇总}$

【主线】

$运动学$

1. 定义标准型及改进型D-H参数，建立机器人模型。
2. 运动学正解
3. 基于蒙特卡罗方法(Monte Carlo Method)构建机器人工作空间

$动力学$
（待补充）

【补充说明】

1. 关于灵活工作空间与可达工作空间的理解
2. 关于改进型D-H参数(modified Denavit-Hartenberg)的详细建立步骤
3. 关于旋转的参数化（欧拉角、姿态角、四元数）的相关问题
4. 关于双变量函数atan2(x,y)的解释
5. 关于机器人运动学反解的有关问题

本文主要讲述Matlab中如何理解和设计六轴机器人的D-H参数、如何建立六自由度机器人模型，后续会对机器人进行正逆解的求解。

---

前言

1.Matlab机器人工具箱

由于我们需要接触Matlab上的机器人工具箱，因此首先先放上下载工具箱的官网，不需要积分，直接从官网上下载，不用担心会出问题。https://petercorke.com/resources/downloads/
相关资源： 若发现无法正常登录该网址，可通过该资源进行下载机器人工具箱压缩包：Matlab机器人工具箱-robot-10.3.1及相关实例.
具体的安装方法已经有朋友说得很清楚了：Matlab机器人工具箱

2.研究对象—六自由度机器人

调出机器人的各连杆参数，根据各连杆的长度和结构可以得出机器人的D-H参数。

随着人工智能的发展，机器人也不断变换着形态出现在人们的眼里，有的表现为餐厅的服务型机器人、有的表现为智能汽车。无一不在昭示着机器人的多用途以及它的多功能，而最典型最基础的的莫过于工业机器人。

---

正文

一、D-H参数(Denavit–Hartenberg parameters)

机械臂的一个重要特征参数就是DH参数。

坐标系建立步骤：

1. 确定Z轴 如果关节是旋转的，Z轴按右手定则大拇指指向为正方向，关节转角θ为关节变量。如果关节是移动的，Z轴定在沿直线运动方向的正方向，连杆偏移d为关节变量。
2. 确定X轴 情况一：两关节Z轴既不平行也不相交，即呈异面直线时。则取两Z轴公垂线方向作为X轴方向。 情况二：两关节Z轴平行。此时，两Z轴之间有无数条公垂线，可挑选与前一关节的公垂线共线的一条公垂线。
   情况三：两关节Z轴相交。则取两条Z轴的叉积方向作为X轴（叉积：向量积）
3. 确定Y轴 通过右手定则确定Y轴的方向。大拇指指向Z轴的方向，以x轴为准，逆时针旋转90°的方向为y轴的方向。

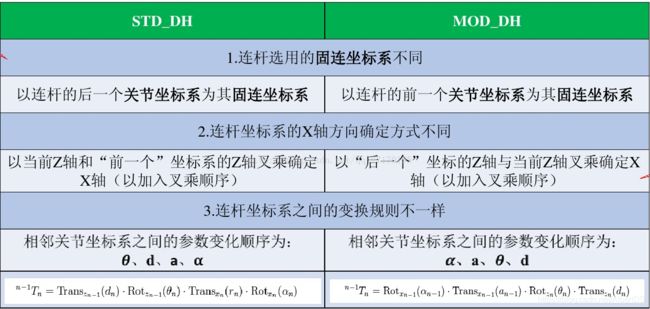
对于标准型和改进型，区别在于固连坐标系不同以及执行变换的的顺序不同。

1.标准型D-H参数(STD)

1. 对于标准型来说，X轴的方向以当前的Z轴和前一个关节的Z轴（也就是Z_i-1轴）的叉乘方向，右手定则：由Z_i-1轴转向Z轴，大拇指方向即为X轴方向。也可以使用简便的方法，由Z_i-1轴指向Z轴，公垂线方向即是X轴的方向。附上更加直观的视频：机器人学DH参数的最直观讲解机器人入门必备
   
2. 建模步骤：
   $（1）绕z_{i-1}轴旋转{\theta }_i，使得x_{i-1}和x_i平行；$
   $（2）沿z_{i-1}轴平移d_i，使得x_{i-1}和x_i重合；$
   $（3）沿x_i轴平移a_i，使得z_{i-1}和z_i重合；$
   $（4）绕x_i轴旋转{\alpha }_i，使得z_{i-1}和z_i共线；$
3. STD-DH方法变换时四个参数相乘的顺序依次为$\theta$→$d$→$a$→$\alpha$
4. 通过每个旋转和平移的步骤得到旋转矩阵
   $Rot(z_{i-1},{\theta }_i)$ = $\left[\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_i& 0& 0\\ sin{\theta }_i& cos{\theta }_i& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$

$Trans(z_{i-1}，d_i)=$ $\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& d_i\\ 0& 0& 0& 1\end{array}\right]$

$Trans(x_i，a_i)=$ $\left[\begin{array}{cccc}1& 0& 0& a_i\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$

$Rot(x_i，{\alpha }_i)=$ $\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cos{\alpha }_i& -sin{\alpha }_i& 0\\ 0& sin{\alpha }_i& cos{\alpha }_i& 0\\ 0& 0& 0& 1\end{array}\right]$

$可以得到变换矩{阵}^{i-1}{T}_i=Rot(z_{i-1},{\theta }_i)\times Trans(z_{i-1}，d_i)\times Trans(x_i，a_i)\times Rot(x_i，{\alpha }_i)$

${}^{i-1}{T}_i=$$\left[\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_{i}cos{\alpha }_i& sin{\theta }_{i}sin{\alpha }_i& a_{i}cos{\theta }_i\\ sin{\theta }_i& cos{\theta }_{i}cos{\alpha }_i& -cos{\theta }_{i}sin{\alpha }_i& a_{i}sin{\theta }_i\\ 0& sin{\alpha }_i& cos{\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right]$

2.改进型D-H参数(MOD)

1. 对于改进型来说，$X$轴的方向以当前的Z轴和后一个关节的$Z$轴（也就是$Z_{i+1}$轴）的叉乘方向，使用右手定则：由Z轴转向$Z_{i+1}$轴，大拇指方向即为$X$轴方向。具体如何建立查看上述的建立步骤，关于$X$轴确定的三种情况。
2. 建模步骤：
   $（1）绕x_i轴旋转{\alpha }_i，使得z_i和z_{i+1}共线；$
   $（2）沿x_i轴平移a_i，使得z_i和z_{i+1}重合$
   $（3）绕z_i轴旋转{\theta }_i，使得x_{i-1}和x_i共线；$
   $（4）沿z_i轴平移d_i，使得x_{i-1}和x_i重合；$
3. MOD-DH方法变换时四个参数相乘的顺序依次为$\alpha$→$a$→$\theta$→$d$
4. 参考正文1.4可得到变换矩阵
   ${}^{i-1}{T}_i=Rot(x_i，{\alpha }_{i-1})\times Trans(x_i，a_{i-1})\times Rot(z_i,{\theta }_i)\times Trans(z_i，d_i)$

${}^{i-1}{T}_i=$$\left[\begin{array}{cccc}cos{\theta }_i& -sin{\theta }_i& 0& a_{i-1}\\ sin{\theta }_{i}cos{\alpha }_{i-1}& cos{\theta }_{i}cos{\alpha }_{i-1}& -sin{\alpha }_{i-1}& -sin{\alpha }_{i-1}{d}_i\\ sin{\theta }_{i}sin{\alpha }_{i-1}& cos{\theta }_{i}sin{\alpha }_{i-1}& cos{\alpha }_{i-1}& cos{\alpha }_{i-1}{d}_i\\ 0& 0& 0& 1\end{array}\right]$

D-H参数是研究各类型机器人的必经之路，只有熟悉构建机器人的DH参数才能更好得对机器人进行正逆解的求解。

二、Link函数与SerialLink函数

Link函数包含与机器人关节和链接相关的所有信息，例如运动学参数，刚体惯性参数，电机和传输参数。
Link函数的各类参数如下：

运动学参数	含义
theta	joint angle 关节转角
d	link offset 连杆偏移
a	link length 连杆长度
alpha	link twist 连杆扭角
jointtype	‘R’ if revolute, ‘P’ if prismatic 旋转关节为R，移动关节为P
mdh	0 if standard D&H, else 1 标准型为0，改进型为1
offset	joint variable offset 关节变量偏移
qlim	joint variable limits [min max] 关节变量极限[min max]

动力学参数	含义
m	link mass 连杆质量
r	link COG wrt link coordinate frame 3x1 连杆相对于坐标系的质心位置 3x1位置矩阵
I	link inertia matrix, symmetric 3x3, about link COG.连杆重心相对于坐标系的惯性矩阵 3x3旋转矩阵
B	link viscous friction (motor referred) 连杆粘性摩擦力(以电机为基准)
Tc	link Coulomb friction 连杆库仑摩擦力
G	gear ratio 齿轮比(传动比)
Jm	motor inertia (motor referred)电机惯量(以电机为基准)

对于只需要把机器人模型建立出来，不考虑机器人的动力学参数的情况，那么只需要用到theta、d、a、alpha和offset等几个参数即可。

---

接下来使用Link函数对D-H参数表进行模型的建立，并通过使用SerialLink函数来将L1 L2 L3 L4 L5 L6连杆连接起来。
对于Link函数来说，无论是标准型还是改进型，参数的顺序都为：关节转角、连杆偏移、连杆长度、连杆扭角。

1.使用标准型D-H参数建立机器人模型

%% STD-DH参数
%定义连杆的D-H参数
%连杆偏移
d1 = 398;
d2 = -0.299;
d3 = 0;
d4 = 556.925;
d5 = 0;
d6 = 165;
%连杆长度
a1 = 168.3;
a2 = 650.979;
a3 = 156.240;
a4 = 0;
a5 = 0;
a6 = 0;
%连杆扭角
alpha1 = pi/2;
alpha2 = 0;
alpha3 = pi/2;
alpha4 = -pi/2;
alpha5 = pi/2;
alpha6 = 0;
%建立机器人模型
%       theta  d        a        alpha    
L1=Link([0     d1       a1       alpha1]);
L2=Link([0     d2       a2       alpha2]);L2.offset = pi/2;
L3=Link([0     d3       a3       alpha3]);
L4=Link([0     d4       a4       alpha4]);
L5=Link([0     d5       a5       alpha5]);
L6=Link([0     d6       a6       alpha6]);
%限制机器人的关节空间
L1.qlim = [(-165/180)*pi,(165/180)*pi];
L2.qlim = [(-95/180)*pi, (70/180)*pi];
L3.qlim = [(-85/180)*pi, (95/180)*pi];
L4.qlim = [(-180/180)*pi,(180/180)*pi];
L5.qlim = [(-115/180)*pi,(115/180)*pi];
L6.qlim = [(-360/180)*pi,(360/180)*pi];
%连接连杆，机器人取名为myrobot
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','myrobot');
robot.plot([0,0,0,0,0,0]);%输出机器人模型，后面的六个角为输出时的theta姿态
robot.display();%打印出机器人D-H参数表
robot.teach;%展示机器人模型
hold on;

2.使用改进型D-H参数建立机器人模型

其中‘modified’的意思是该机器人使用改进型D-H参数表来建立模型。

%% MOD-DH参数
%定义连杆的D-H参数
%连杆偏移
d1 = 398;
d2 = -0.299;
d3 = 0;
d4 = 556.925;
d5 = 0;
d6 = 165;
%连杆长度
a1 = 0;
a2 = 168.3;
a3 = 650.979;
a4 = 156.240;
a5 = 0;
a6 = 0;
%连杆扭角
alpha1 = 0;
alpha2 = pi/2;
alpha3 = 0;
alpha4 = pi/2;
alpha5 = -pi/2;
alpha6 = pi/2;
%建立机器人模型
%       theta  d        a        alpha     
L1=Link([0     d1       a1       alpha1     ],'modified');
L2=Link([0     d2       a2       alpha2     ],'modified');L2.offset = pi/2;
L3=Link([0     d3       a3       alpha3     ],'modified');
L4=Link([0     d4       a4       alpha4     ],'modified');
L5=Link([0     d5       a5       alpha5     ],'modified');
L6=Link([0     d6       a6       alpha6     ],'modified');
%限制机器人的关节空间
L1.qlim = [(-165/180)*pi,(165/180)*pi];
L2.qlim = [(-95/180)*pi, (70/180)*pi];
L3.qlim = [(-85/180)*pi, (95/180)*pi];
L4.qlim = [(-180/180)*pi,(180/180)*pi];
L5.qlim = [(-115/180)*pi,(115/180)*pi];
L6.qlim = [(-360/180)*pi,(360/180)*pi];
%连接连杆，机器人取名为myrobot
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','myrobot');
robot.plot([0,0,0,0,0,0]);%输出机器人模型，后面的六个角为输出时的theta姿态
robot.display();%打印出机器人D-H参数表
robot.teach;%展示机器人模型
hold on;

注解：L2.offset = pi/2的意思为第二根轴相对于第一根轴有90度的关节偏移量，也就是初始状态下连杆2对于连杆1来说有一个关节的偏置。

接下来看添加关节偏移量与不添加的区别：
添加入关节偏移量
不添加关节偏移量

可以看出关节偏置的添加与否对于机器人末端位置来说差别还是蛮大的

---

参考资料

1. Matlab机器人工具箱（1）——机器人的建立、绘制与正逆运动学
2. Matlab机器人工具箱
   
3. 标准DH和改进DH的区别
4. 标准DH建模与改进DH建模
   
5. 浅谈标准DH（SDH）和改进DH（MDH）
   
6. Denavit–Hartenberg参数