【Matlab 六自由度机器人】基于蒙特卡罗方法(Monte Carlo Method)构建机器人工作空间(附MATLAB建模仿真完整代码)
【Matlab 六自由度机器人】基于蒙特卡洛法构建工作空间
- 往期回顾
- 前言
- 正文
-
- 一、蒙特卡洛方法及机器人工作空间的概述
-
- 1. 蒙特卡洛法
- 2. 机器人工作空间
- 二、rand函数的应用
-
- 1. rand函数
- 2. 随机画点
- 三、基于蒙特卡洛法采用运动学正解构建工作空间
-
- 1. 运动学正解
- 2. 构建工作空间
- 3. 代码运行结果
- 总结
- 参考资料
往期回顾
【Matlab 六自由度机器人】
1. 建立机器人模型
2. 运动学正解
前言
本文主要介绍如何在MATLAB中实现蒙特卡洛随机采样的方法,对每个关节在其角度范围内随机选取大量的采样点,并进行正运动学求解计算得到相应的末端位置,并绘制末端位置点,进行机器人工作空间的可视化。
本篇文章分为两个部分的内容,第一个部分阐述蒙特卡洛方法Monte Carlo Method和机器人工作空间的基本特点,第二部分解析代码的实现。
正文
一、蒙特卡洛方法及机器人工作空间的概述
机器人的工作空间是评估机械臂工作性能的优劣的重要指标,分析机械臂工作空间的方法有以下三种:几何构建法、解析法和数值计算法。
蒙特卡洛法就是数值计算法的其中一种,该方法是随机选取大量的采样点,来尽可能构建出机器人完整的工作空间。
1. 蒙特卡洛法
机械臂工作空间的求解方法主要有图解法、解析法和数值法。而图解法和解析法都受关节数目的限制,对于有些机械臂无法准确描述,数值法计算量太大,对于有些边界曲面可靠性得不到保证。因此采用从数值法衍生发展出来的基于随机概率的算法:蒙特卡洛法。
蒙特卡洛法( Monte Carlo method) ,又称统计模拟法,是借助于随机抽样( 伪随机数)来解决数学问题的数值方法,在工程上被广泛应用于描述某些随机的物理现象。该方法易实现图形显示功能,计算速度快、简单,省却了繁复的数学推导和演算过程,适合于任何关节型机械臂工作空间的求解,对关节变量的变化范围没有限制,其误差也与维数无关。
蒙特卡洛法应用于机械臂工作空间求解的基本思想
- 机械臂的各关节是在其相应取值范围内工作;
- 所有关节在相应取值范围内随机遍历取值;
- 末端点的所有随机值的集合就构成了机械臂的工作空间。
2. 机器人工作空间
机器人的工作空间(workspace)是指当机器人执行所有可能动作时,其末端执行器扫过的总体空间体积。工作空间受限于机器人的几何结构以及各关节上的机械限位。例如六自由度机器人的每个关节都受不同的角度的限制,如往期文章:建立机器人模型中的 qlim 函数,对6R型机器人的不同的关节都进行了不同程度上的限位。
L1.qlim = [(-165/180)*pi,(165/180)*pi];
L2.qlim = [( -95/180)*pi, (70/180)*pi];
L3.qlim = [( -85/180)*pi, (95/180)*pi];
L4.qlim = [(-180/180)*pi,(180/180)*pi];
L5.qlim = [(-115/180)*pi,(115/180)*pi];
L6.qlim = [(-360/180)*pi,(360/180)*pi];
工作空间一般可以分为可达工作空间和灵活工作空间。
可达工作空间指机器人可以抵达的所有点的集合,灵活工作空间指机器人可以任意姿态抵达的所有点的集合。显然,灵活工作空间是可达空间的一个子集。因此,本篇文章的主要内容及编程重点在可达工作空间。
二、rand函数的应用
1. rand函数
对于蒙特卡洛法的随机性,我们采用 rand()函数来进行表示。以下是对 rand()函数的转述。如需更详细的解释,请前往MATLAB官网的均匀分布的随机数
rand()函数的语法有如下几种:
| 语法 | 说明 |
|---|---|
| X = rand | 返回一个在区间 (0,1) 内均匀分布的随机数 |
| X = rand(n) | 返回一个 n×n 的随机数矩阵 |
| X = rand(sz1,…,szN) | 返回由随机数组成的 sz1×…×szN 数组,其中 sz1,…,szN 指示每个维度的大小。例如:rand(3,4) 返回一个 3×4 的矩阵 |
| X = rand(sz) | 返回由随机数组成的数组,其中大小向量 sz 指定 size(X)。例如:rand([3 4]) 返回一个 3×4 的矩阵 |
| X = rand(___,typename) | 返回由 typename 数据类型的随机数组成的数组。typename 输入可以是 ‘single’ 或 ‘double’。您可以使用上述语法中的任何输入参数 |
| X = rand(___,‘like’,p) | 返回由 p 等随机数组成的数组;也就是与 p 同一对象类型。您可以指定 typename 或 ‘like’,但不能同时指定两者 |
| X = rand(s,___) | 从随机数流 s 而不是默认全局流生成数字。要创建一个流,请使用 RandStream。指定 s,后跟上述语法中的任意参数组合,但涉及 ‘like’ 的组合除外。此语法不支持 ‘like’ 输入 |
注意!
不建议对 rand 函数使用 ‘seed’、‘state’ 和 ‘twister’ 输入。
2. 随机画点
了解了上述的 rand()函数,下面进行机器人在其角度范围内的关节角度的随机数选取,其通用代码如下:
thetamin*(pi/180) + (thetamax-thetamin)*(pi/180)*rand;
该代码的含义是:以角度范围的最小值为基础,加上角度范围内的随机数,就得到当前该轴的关节随机角度值。
三、基于蒙特卡洛法采用运动学正解构建工作空间
1. 运动学正解
在这里就直接贴代码脚本了,若有兴趣了解运动学正解,请前往往期文章【Matlab 六自由度机器人】运动学正解
脚本如下:
function [T06] = MODtransmatrix(theta1,theta2,theta3,theta4,theta5,theta6)
%%
%连杆偏移
d1 = 398;
d2 = -0.299;
d3 = 0;
d4 = 556.925;
d5 = 0;
d6 = 165;
%连杆长度
a1 = 0;
a2 = 168.3;
a3 = 650.979;
a4 = 156.240;
a5 = 0;
a6 = 0;
%连杆扭角
alpha1 = 0;
alpha2 = pi/2;
alpha3 = 0;
alpha4 = pi/2;
alpha5 = -pi/2;
alpha6 = pi/2;
MDH = [theta1 d1 a1 alpha1;
theta2+pi/2 d2 a2 alpha2;
theta3 d3 a3 alpha3;
theta4 d4 a4 alpha4;
theta5 d5 a5 alpha5;
theta6 d6 a6 alpha6];
T01=[cos(MDH(1,1)) -sin(MDH(1,1)) 0 MDH(1,3);
sin(MDH(1,1))*cos(MDH(1,4)) cos(MDH(1,1))*cos(MDH(1,4)) -sin(MDH(1,4)) -sin(MDH(1,4))*MDH(1,2);
sin(MDH(1,1))*sin(MDH(1,4)) cos(MDH(1,1))*sin(MDH(1,4)) cos(MDH(1,4)) cos(MDH(1,4))*MDH(1,2);
0 0 0 1];
T12=[cos(MDH(2,1)) -sin(MDH(2,1)) 0 MDH(2,3);
sin(MDH(2,1))*cos(MDH(2,4)) cos(MDH(2,1))*cos(MDH(2,4)) -sin(MDH(2,4)) -sin(MDH(2,4))*MDH(2,2);
sin(MDH(2,1))*sin(MDH(2,4)) cos(MDH(2,1))*sin(MDH(2,4)) cos(MDH(2,4)) cos(MDH(2,4))*MDH(2,2);
0 0 0 1];
T23=[cos(MDH(3,1)) -sin(MDH(3,1)) 0 MDH(3,3);
sin(MDH(3,1))*cos(MDH(3,4)) cos(MDH(3,1))*cos(MDH(3,4)) -sin(MDH(3,4)) -sin(MDH(3,4))*MDH(3,2);
sin(MDH(3,1))*sin(MDH(3,4)) cos(MDH(3,1))*sin(MDH(3,4)) cos(MDH(3,4)) cos(MDH(3,4))*MDH(3,2);
0 0 0 1];
T34=[cos(MDH(4,1)) -sin(MDH(4,1)) 0 MDH(4,3);
sin(MDH(4,1))*cos(MDH(4,4)) cos(MDH(4,1))*cos(MDH(4,4)) -sin(MDH(4,4)) -sin(MDH(4,4))*MDH(4,2);
sin(MDH(4,1))*sin(MDH(4,4)) cos(MDH(4,1))*sin(MDH(4,4)) cos(MDH(4,4)) cos(MDH(4,4))*MDH(4,2);
0 0 0 1];
T45=[cos(MDH(5,1)) -sin(MDH(5,1)) 0 MDH(5,3);
sin(MDH(5,1))*cos(MDH(5,4)) cos(MDH(5,1))*cos(MDH(5,4)) -sin(MDH(5,4)) -sin(MDH(5,4))*MDH(5,2);
sin(MDH(5,1))*sin(MDH(5,4)) cos(MDH(5,1))*sin(MDH(5,4)) cos(MDH(5,4)) cos(MDH(5,4))*MDH(5,2);
0 0 0 1];
T56=[cos(MDH(6,1)) -sin(MDH(6,1)) 0 MDH(6,3);
sin(MDH(6,1))*cos(MDH(6,4)) cos(MDH(6,1))*cos(MDH(6,4)) -sin(MDH(6,4)) -sin(MDH(6,4))*MDH(6,2);
sin(MDH(6,1))*sin(MDH(6,4)) cos(MDH(6,1))*sin(MDH(6,4)) cos(MDH(6,4)) cos(MDH(6,4))*MDH(6,2);
0 0 0 1];
T06 = T01*T12*T23*T34*T45*T56;
end
注意!!!
这里的theta2+pi/2是由于机器人在第二个关节有90°的关节偏移量,因此需要在theta2上加上pi/2。
2. 构建工作空间
对各关节进行一个角度值的限位,再通过第三章第1节的运动学正解中的MODtransmatrix脚本,得到机器人的末端位置,最后通过plot3()函数进行图像的绘制,最终的到机器人近似的工作空间。
代码如下:
theta1min = -165;theta1max = 165;
theta2min = -95 ;theta2max = 70 ;
theta3min = -85 ;theta3max = 95 ;
theta4min = -180;theta4max = 180;
theta5min = -115;theta5max = 115;
theta6min = -360;theta6max = 360;
%
n = 30000;
x = zeros;y = zeros;z = zeros;
for i = 1:n
theta1 = theta1min*(pi/180) + (theta1max-theta1min)*(pi/180)*rand;
theta2 = theta2min*(pi/180) + (theta2max-theta2min)*(pi/180)*rand;
theta3 = theta3min*(pi/180) + (theta3max-theta3min)*(pi/180)*rand;
theta4 = theta4min*(pi/180) + (theta4max-theta4min)*(pi/180)*rand;
theta5 = theta5min*(pi/180) + (theta5max-theta5min)*(pi/180)*rand;
theta6 = theta6min*(pi/180) + (theta6max-theta6min)*(pi/180)*rand;
Tws = MODtransmatrix(theta1,theta2,theta3,theta4,theta5,theta6);
x(i) = Tws(1,4);
y(i) = Tws(2,4);
z(i) = Tws(3,4);
end
figure('color',[1 1 1]);
plot3(x,y,z,'b.','MarkerSize',0.5)
hold on
xlabel('x轴(millimeter)','color','k','fontsize',15);
ylabel('y轴(millimeter)','color','k','fontsize',15);
zlabel('z轴(millimeter)','color','k','fontsize',15);
grid on
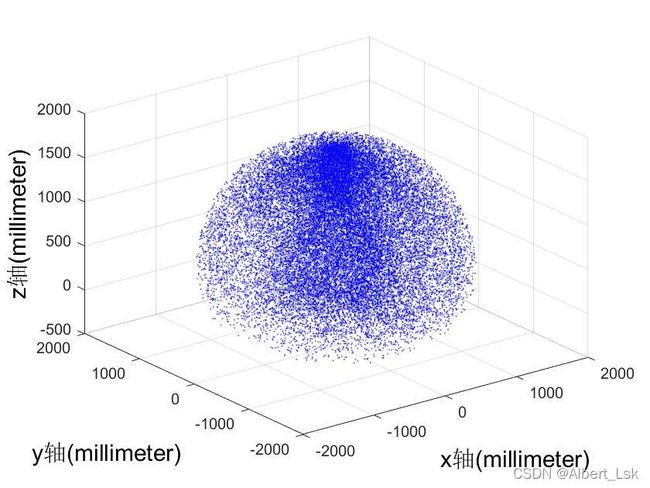
3. 代码运行结果
总结
本文主要介绍了如何在MATLAB中实现蒙特卡洛随机采样的方法,对每个关节在其角度范围内随机选取大量的采样点,并进行正运动学求解计算得到相应的末端位置,并根据末端位置点的绘制,构建了机器人工作空间。
参考资料
1. 蒙特卡洛法之MATLAB实现
2. 蒙特卡罗法
3. 蒙特卡罗算法是什么?
4. 机械臂——六轴机械臂操作空间运动分析
5. 机器人工作空间可视化(蒙特卡罗法)
6. 基于蒙特卡洛法的七自由度拟人机械臂工作空间分析