层次分析法
层次分析法
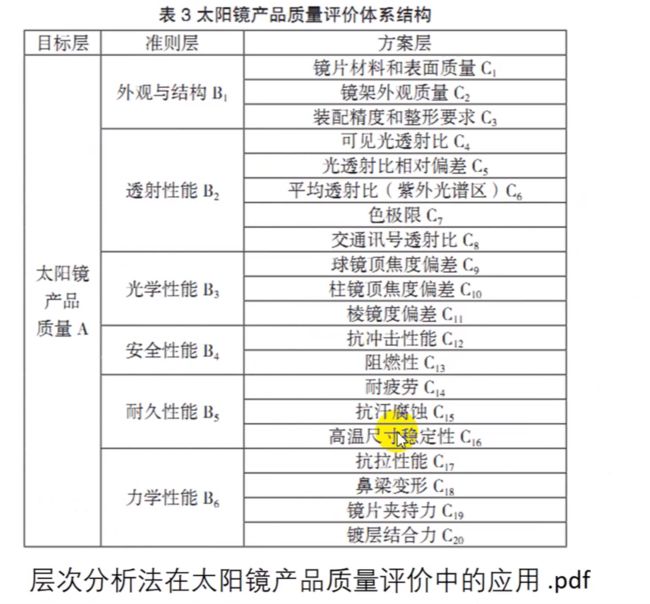
2012a 国赛论文也可以使用了层次分析法来计算权重。
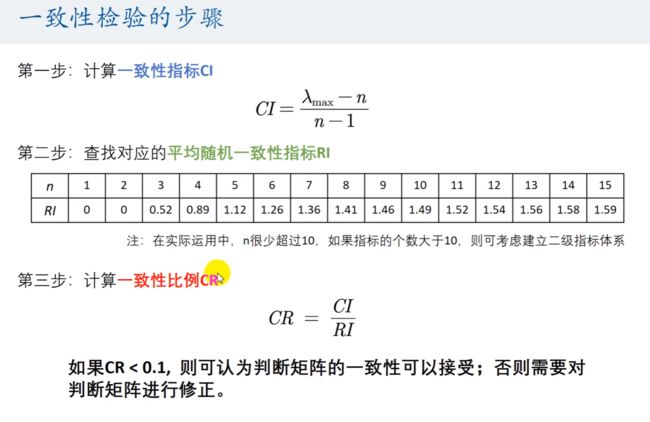
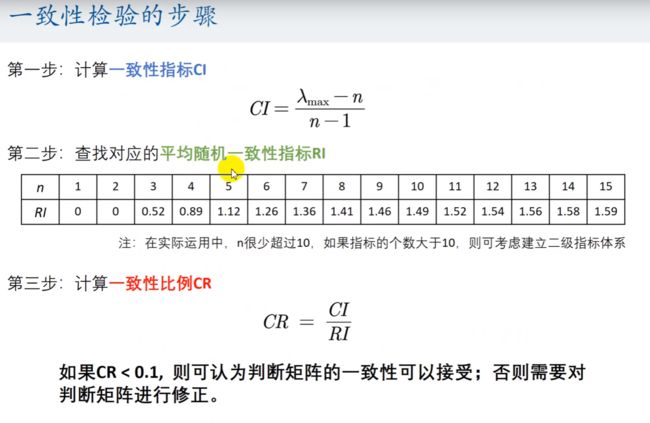
平均随机一致性指标
RI = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 0.49, 0.52, 1.54, 1.56, 1.58, 1.59];
一共 15 个。
层次分析法（The analytic hierarchy process，AHP）是建模比赛最基础的模型之一，其主要用于解决评价类问题（例如：选择哪种方案最好、哪位运动员或者员工表现的更优秀）。
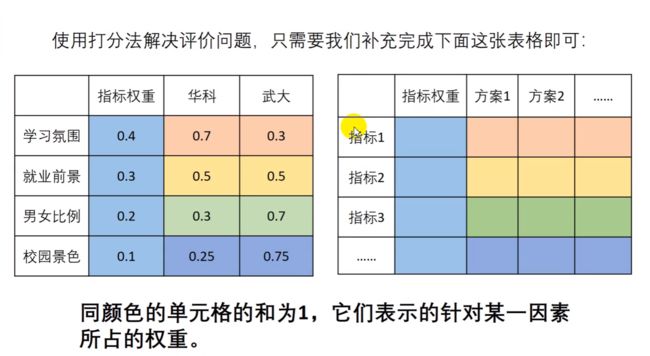
权重 即重要性程度
权重表如下：
引出层次分析法
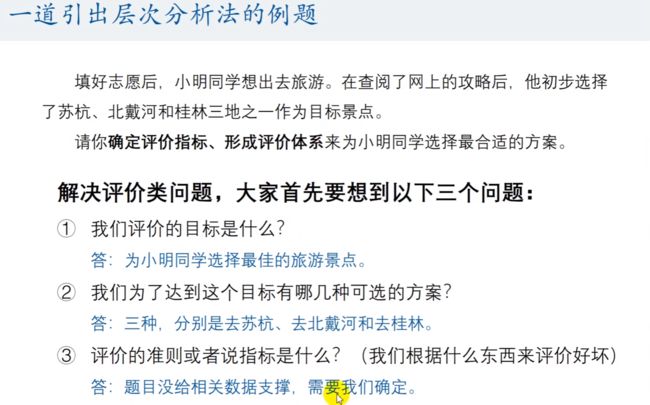
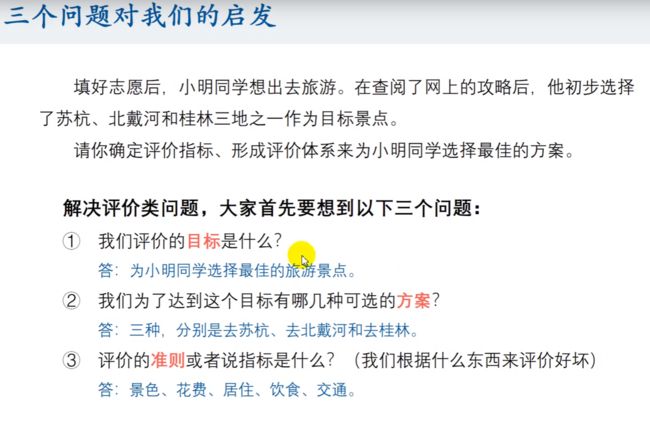
当题目让你 确定评价指标、形成评价体系 时，那么这就是一个评价类问题，一定要首先想到 3 个问题：
- 我们评价的目标是什么？
- 我们为了达到这个目标有哪几种可选的方案？
- 评价的准则或者说指标是什么？（我们根据什么东西来评价好坏）（一般题目中不会告诉你准则或指标）
例题：
一般而言，前两个问题的答案是显而易见的，第三个问题的答案需要我们根据题目中的背景材料、常识以及 网上搜集到的参考资料 进行结合，从中筛选出最合适的指标。
怎么在网上搜索参考资料？
优先选择知网（或者万方、百度学术、谷歌学术等平台）搜索相关文献。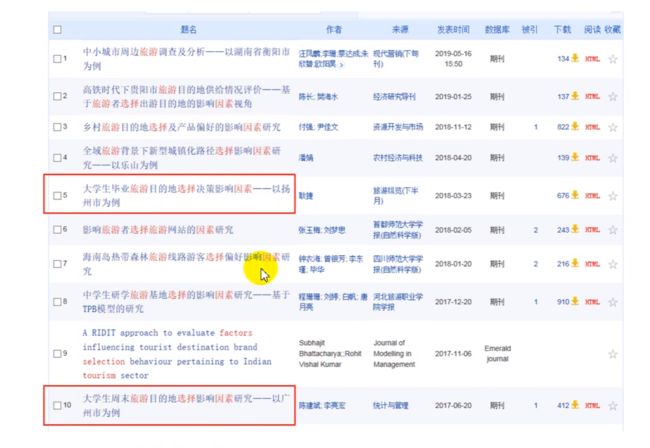
因为引用别人的论文 会显得很专业 ，另外别人的研究方法也可以借鉴，因为你们的研究方向差不多。
没有相关文献怎么办？
**强烈推荐一个很腻害的网站：**虫部落快搜
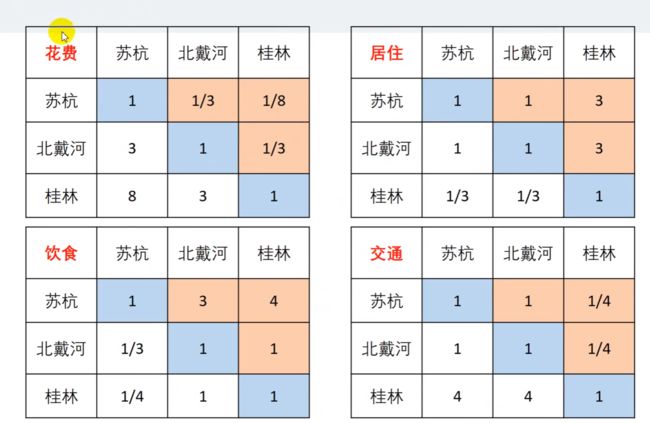
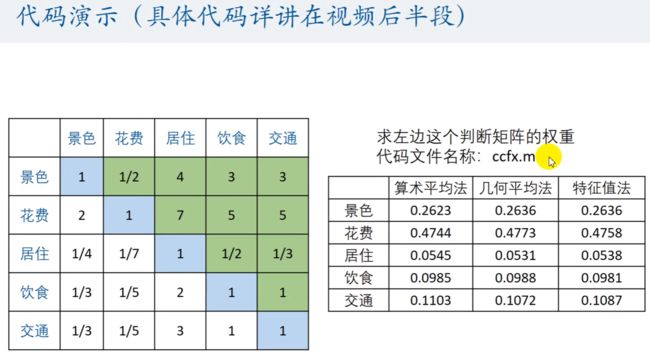
假设之前的例题中，我们已经搜索到了要从 景色、花费、居住、饮食 和 交通来进行评价，所以我们可以使用 权重表。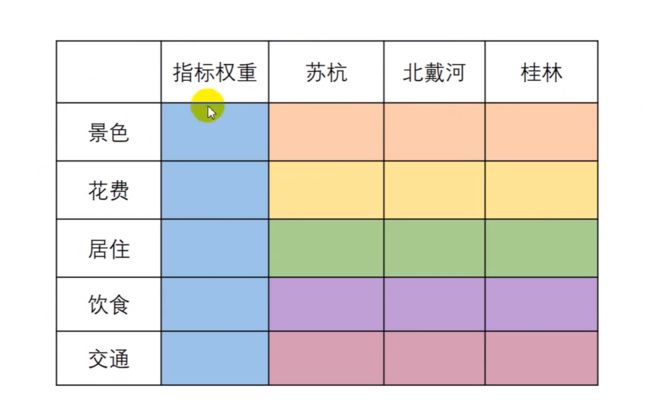
怎么获得每个单元格（因子）的权重？
当然，不能直接问小明，因为这样往往比较片面和不周全（说不定，隔一天问他答案可能就变了）
采用分而治之的思想
分而治之：我们先来确定权重图中指标的权重。
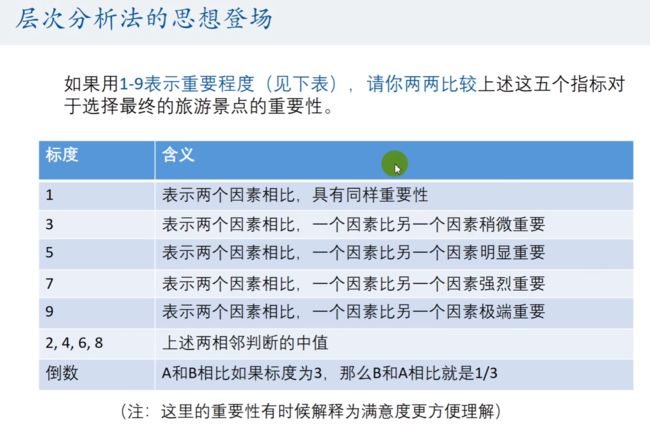
但是，一次性考虑景色、花费、居住、饮食 和 交通这五个指标之间的关系，往往考虑不周。因此，**我们两个两个指标进行比较，最终根据两两比较的结果来推算出权重（这就是层次分析法的思想）。**在本次例题中，一共需要比较的次数为： 组合数 ==》C52 ，即 5! / (2! * 3!) = 10。
层次分析法设置权重时的规则：
首先，你要知道，小明对于一个景点，认为哪几个因素最重要。
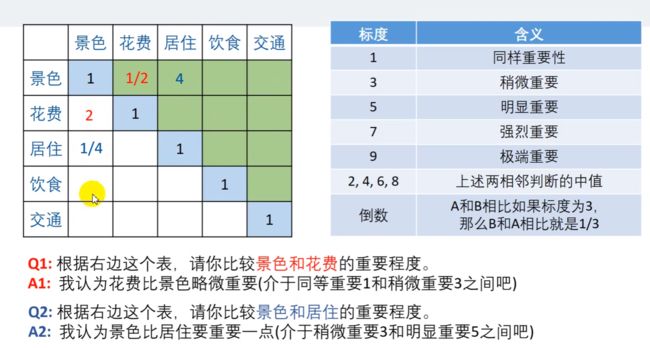
比如此例题，我们要绘制一个方阵（行和列数相等的矩阵），此矩阵的主对角线元素全部为 1，这是因为 比较两个一模一样的元素是，比值当然是 1，都一样重要。
我们只需要算矩阵中一半的元素，另外一半完全可以取倒数。在线性代数中，这个方阵叫做 正 互反矩阵。而实际上，用层次分析法的角度来看，上述矩阵就被称为 判断矩阵。（要记住这些矩阵的特点）
得到了判断矩阵，就可以计算出权重了。
我们刚才填写的是指标的判断矩阵，用于获得指标的权重。但是我们还没有获得关于任意一个指标（比如 景色），对于不同的旅游景点的判断矩阵。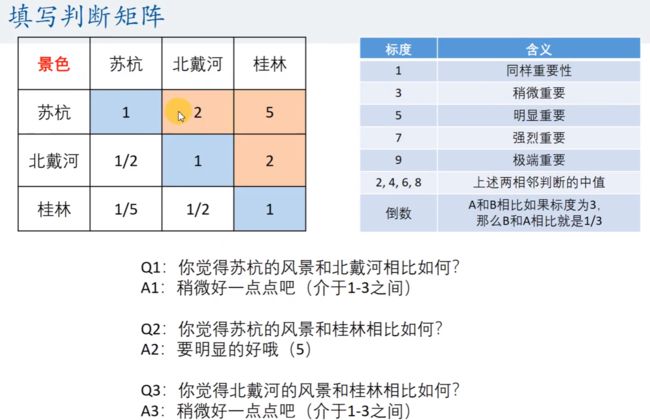
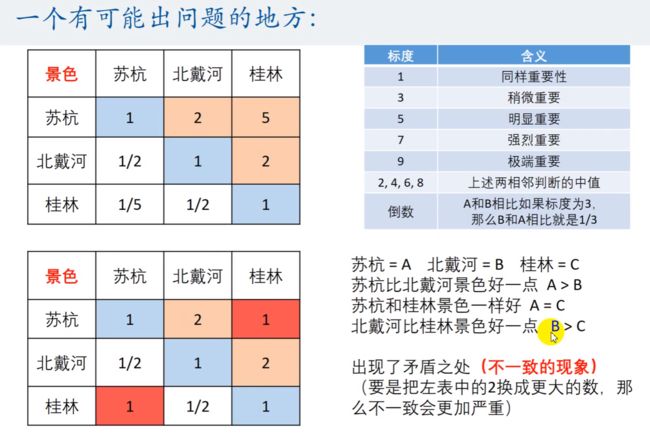
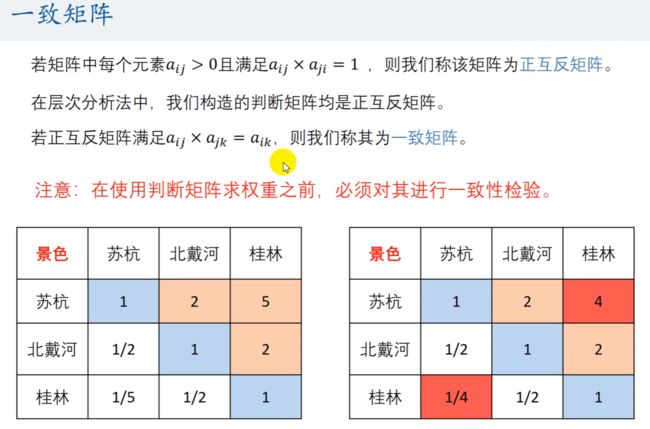
其他比较因素的判断矩阵。
但是，获得表之后，我们会发现，很有可能有 bug。比如上表：
A > B，A = C，但是 B > C。这显然自相矛盾。因此，我们介绍 一致矩阵来解决 bug 问题。
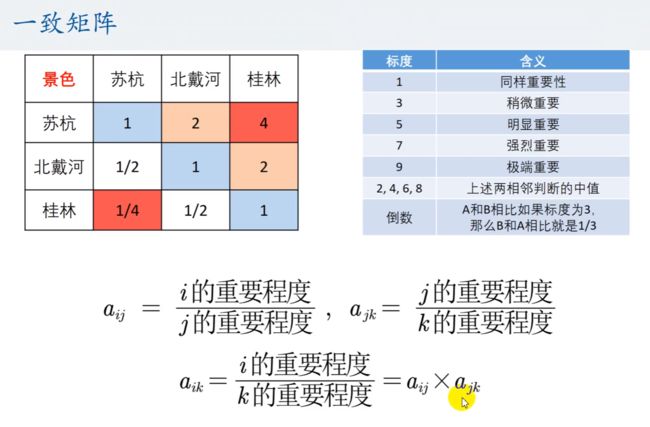
一致性矩阵解决 bug
比如说， a(1, 3)。
a(1, 3) 应当等于 a(1, x) * a(x, 3)。
但是，在出 bug 的矩阵中，a(1, 3) != a(1, 2) * a(2, 3)，a(1,3) = 5而 a(1, 2) * a(2, 3) = 4。
一致矩阵，各行和各列之间，一定是成倍数关系的。
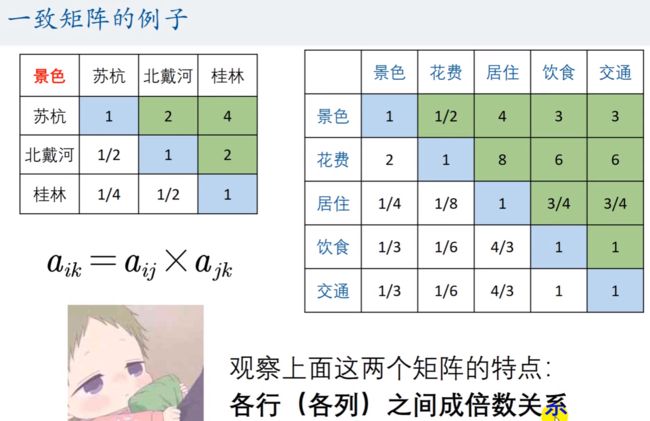
一致矩阵的定义
实际上，可以直接通过判断各行或者各列之间是否成倍数关系即可判断是否为一致矩阵。
绝对的一致，往往是不现实的。我们需要将不一致控制在一个程度之内。
一致性检验
原理：检验我们构造的判断矩阵和一致矩阵是否有太大的差别。
λ 为判断矩阵的特征值。
一致性检验的步骤
平均随机一致性指标 RI 如何计算？
为什么要这样构造 CI，为什么要以 0.1 为划分依据？
结论：
一致性矩阵如何计算权重？
假设我们的判断矩阵已经通过了一致性检验，那么怎么通过判断矩阵获得权重？
看一致性矩阵的每一列（或 每一行）来计算不同旅游景点的权重。权重一定要进行归一化处理：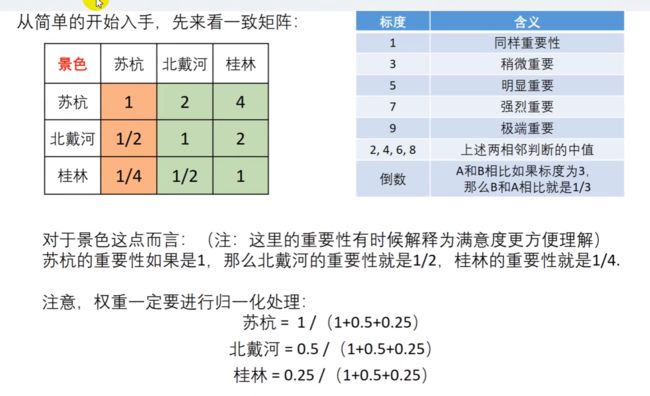
因为一致性矩阵的不同列成倍数关系，所以权重的总和，一定为 1 ，我们也只需要计算其中的一列信息即可。
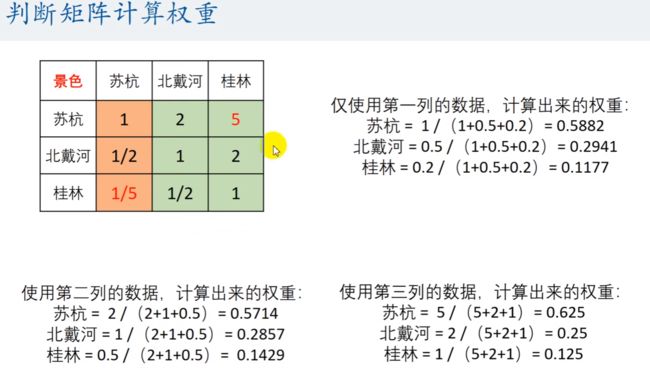
但是 判断矩阵 又该如何计算权重呢？
因为 判断矩阵 不同行、列之间往往不成倍数关系，所以我们需要用到所有的信息。
-
首先计算所有列（或行）的权重。
-
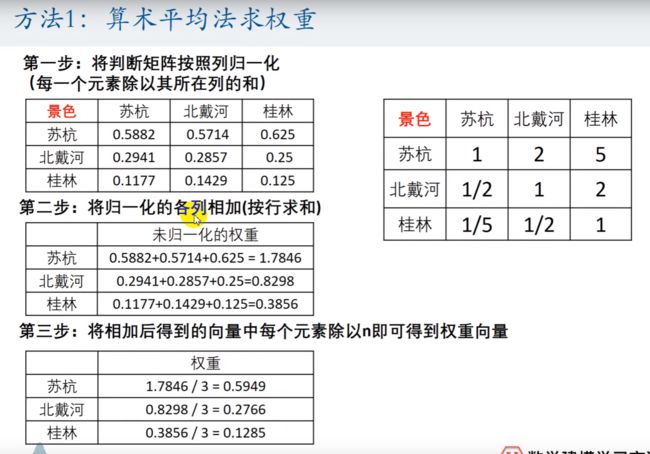
方法1 ：算术平均法求权重
以上步骤，可以写入论文中，但是要将文字叙述，转化为数学描述。
-
方法2：几何平均法求权重（与算术平均法没有太大的区别）
-
方法3：特征值法求权重（最常用，国赛一般都使用这种方法）
如果判断矩阵的一致性可以接收，那么就可以使用第一列的向量即最大特征值对应的特征向量就可以代表它的权重。
-
将计算结果填入权重表中
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-yN9j2Jc2-1600182789478)(C:\Users\Sun and Snow\AppData\Roaming\Typora\typora-user-images\image-20200706104958573.png)]
使用 matlab 计算权重
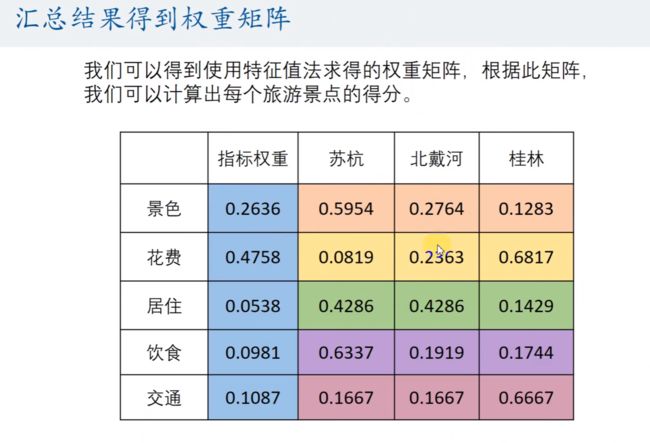
汇总结果得到权重矩阵
计算各方案的得分
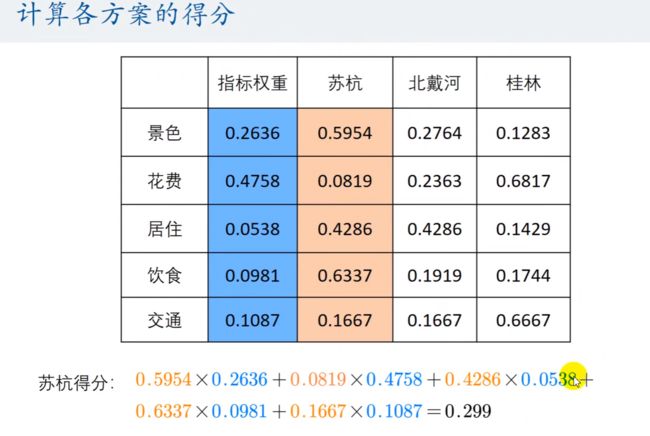
如何快速计算最终得分？
- 可以使用 C++ 二维数组，将元素录入，然后逐个计算；
- 可以使用 matlab 关于矩阵元素的计算方法；
- 可以使用 excell 表（啊，不会~）。
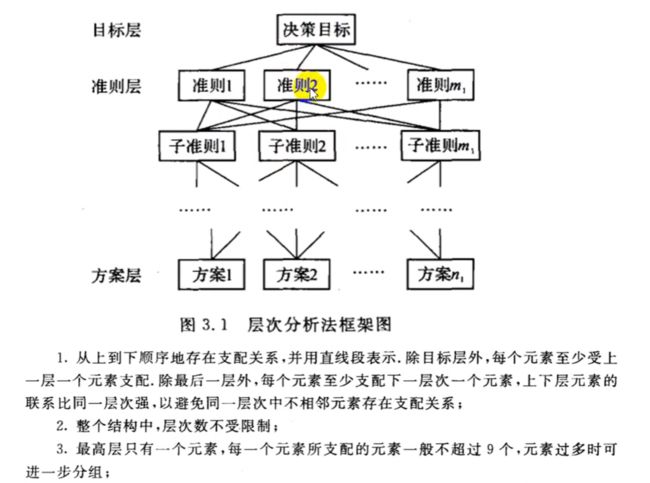
层次分析法步骤
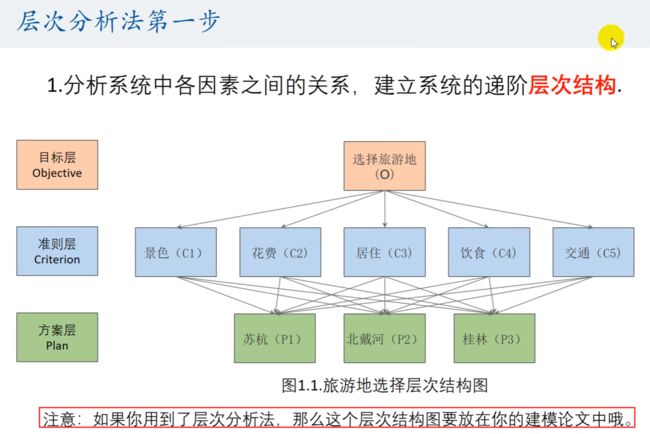
层次分析法第一步
如果使用了层次分析法，一定要在论文中画层次结构图。
准则层其实可以有多个：
更特殊的，一个准则可以对应多个方案，比如：
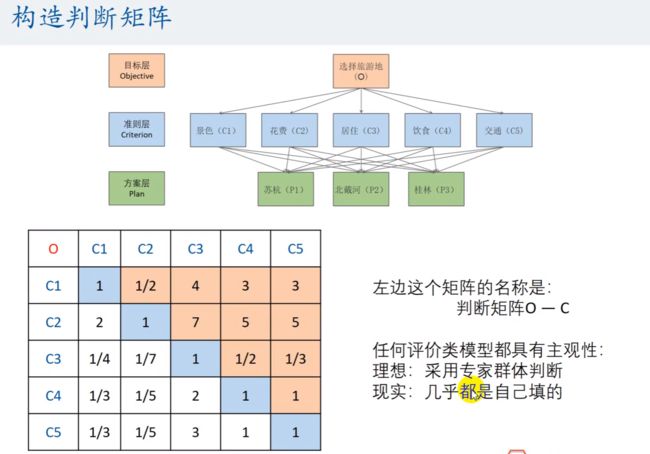
构造判断矩阵
判断矩阵中的数值如果能找到现实数据，那当然最好。要是找不到只能自己填写合理数值，论文中不说明数据怎么来的即可混一下。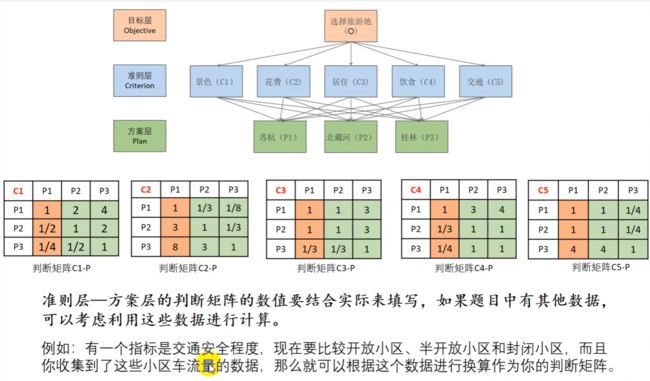
第三步，计算权重
计算各层元素对系统目标的合成权重，并进行排序
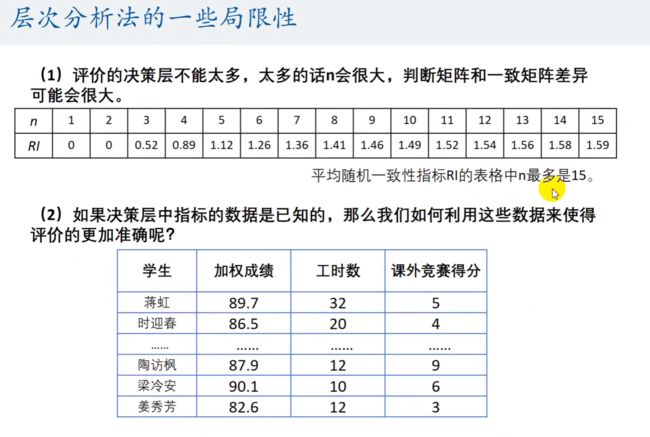
层次分析法的局限性
评价的决策层不能太多，n 最多为 15
如果决策层中的指标数据已知，也不能用层次分析法，因为我们的判断矩阵是自己填写的。
别人论文的可取之处
为了减少查重，还是得用自己的语言来写的。
参考视频