拓扑排序详解

提示：古人学问无遗力 少壮功夫老始成，纸上得来终觉浅 觉知此事须躬行

---

一、AOV网的特点

1、若是从i到j有有一条有向路径，则i是j的前驱，j是i的后继
2、若 是网中有向边，则i是j的直接前驱，j是i的直接后继
3、AOV网中不允许有回路，因为如果有回路存在，则表明某项活动以自己为先决条件，显然不可能

二、问题

我们要解决如下两个问题
1、如何进行拓扑排序
2、如何判别AOV网中是否存在回路

三、拓扑排序

在AOV网没有回路的前提下，我们将全部活动排列成一个线性序列，使得AOV网中有弧存在 则在这个序列中，i 一定排在j的前面 具有这种线性序列称为拓扑有序序列，相应的拓扑有序排序的算法称为拓扑排序

四、拓扑排序的方法

1、在有向图中选一个没有前驱的顶点且输出
2、从图中删除该顶点和所有以他为尾的弧
3、重复上述步骤，直到所有的顶点均已输出，或者当图中不存在无前驱的顶点为止

比如我们要对上述图进行拓扑排序 第一次寻找的是A这一个结点 因为A没有前驱 接下来就是删除A以及以A为弧尾的弧，此时就是如下图

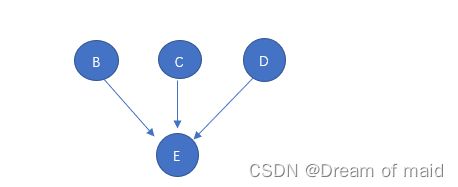
在从中选择一个没有前驱的结点，这里BCD 都可以，这里我们就选择B 同样的道理 删除B以及以B为弧尾的弧此时就是如下图

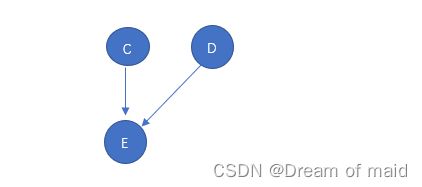
同样的道理 再选一个C删除以C为弧尾的弧

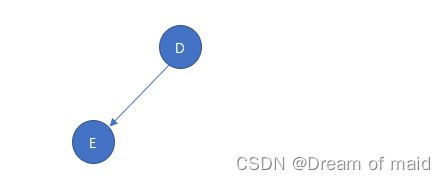
再删除 D

再删除E
所有总的拓扑排序是 当然排序可能不止一种 因为可能不止一个结点在某一步骤中是无前驱的
ABCDE 有人可能会说了这个图太简单了，能不能难一点的图来拓扑
如下

拓扑排序可以如下
AEBDC
EABDC
AEDBC
EADBC

五、检查AOV网中是否存在一个环

对有向图构造其顶点的拓扑有序序列，若是网中所有顶点都在它的拓扑有序序列中，则该AOV 网必定不存在环 若是最后还剩下几个顶点必然是存在环，如下图

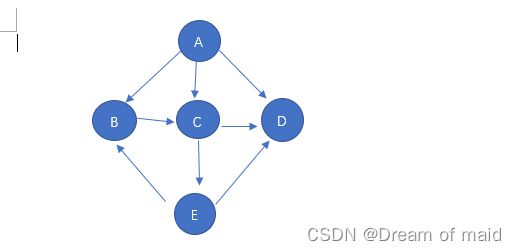
第一次我们删除的是A 第二次我们就找不到没有前驱的节点了 所以就可以判断是存在回路的

六、两种思路

6.1、思路一

1、需要知道那些结点没有前驱 也就是入度为零 怎么找到呢？
本来想着可以使用逆邻接表来实现 不过也确实可以 但是这里依然使用邻接矩阵的方式
我们知道存储有向图的时候 邻接矩阵中行表示的是每一个结点的出度，那么列其实自然就是每一个结点的入度了 这样我们使用一个for就可以知道哪一个结点的入度为零了 但是这样其实你也可以感觉到没有逆邻接表高效， 所以使用另外一种方式就是使用一个count数组来记录每一个结点当前的入度 这样在遍历的过程中一直修改count[]数组 并查看count数组中为零的可以输出 并将其中的值设置为一个标记 比如说-1 表示结点已经被删除 当count数组中的所有的count都为-1时也就可以跳出循环
2、如何删除顶点对应的出度
通过查看邻接矩阵，可以知道与待删除结点关联的结点，此时将对应的结点的count[]中的值减一即可

6.1.1、思路一代码实现

这里我使用了许多的日志 方便进行代码的调试 当时同样的很影响运行的时间

void TopologicalSort(AMGraph &G){
	int count[G.vexnum]={0};
	//初始状每一个结点的入度 也就是计算出count数组
	//通过计算邻接矩阵中每一列 来统计入度 
	for(int i=0;i<G.vexnum;i++){
		for(int j=0;j<G.vexnum;j++){
			if(G.arcs[j][i])count[i]++;
		} 
	} 
	//从中选择一个入度为零的 
	int i=0; vector<char> V;
	for(int x=0;x<G.vexnum;x++){//表示要循环的次数 
	 	int i=0; 
		while(count[i++]!=0);
		if(i>G.vexnum){//说明没有找到的 此时就要退出了  但是还需要判断是因为环才退出的 还是遍历完成 
			cout<<"存在环"<<endl; 
			return;
		} 
		else{//找到待删除的点  将其count置为-1 并将其关联的count数目减一 
			count[i-1]=-1;//-1是作为一种标记
			cout<<"将"<<G.vexs[i-1]<<"加入到容器中"<<endl; 
			V.push_back(G.vexs[i-1]); 
			for(int j=0;j<G.vexnum;j++){
				if(G.arcs[i-1][j]){//若是存在边，则将边删除 并处理count数组 
					//G.arcs[i-1][j]=0;
					count[j]-=1; 
				}
			} 
		} 
		cout<<"此时的count数组是"<<endl; 
		for(int H=0;H<G.vexnum;H++){
			cout<<count[H]<<" "; 
		}
		cout<<endl;
	}
		for(int i=0;i<G.vexnum;i++){
			cout<<V[i]<<" ";
		}
		cout<<endl;
}

6.1.2、思路一运行截图

使用用图就是上述的两个图
输入方式

第一个图的运行结果

第二个有环图的运行结果

6.2、思路二

使用栈（或者队列）的结构：首先计算所有顶点的初始入度，然后将count初值为零的顶点全部入栈，再将栈中的顶点依次出栈（出栈的同时修改其所有邻接顶点的入度，若为零则邻接顶点也入栈）。由于有n个顶点，因此出栈的操作应该循环n次；若在少于n次时栈已经空了，说明图中存在回路。这种方式较上种优化的地方是 不需要每一次都查找哪一个count==0 了

6.2.1、思路二代码

void TopologicalSort(AMGraph &G){
	int count[G.vexnum]={0};
	vector<char> result;//用来存放结果 
	stack<int> S;//定义一个栈 其中存放count值为零的角标 
	//初始状每一个结点的入度 也就是计算出count数组
	//通过计算邻接矩阵中每一列 来统计入度 
	for(int i=0;i<G.vexnum;i++){
		for(int j=0;j<G.vexnum;j++){
			if(G.arcs[j][i])count[i]++;
		} 
	} 
	//将可以此时count==0的结点 也就是可以遍历的放入栈中 
	for(int i=0;i<G.vexnum;i++){
		if(0==count[i]){
			cout<<"将"<<G.vexs[i]<<"放入栈中"<<endl; 
			S.push(i);
		}
	} 
	for(int h=0;h<G.vexnum;h++){//n个结点需要执行n次 
		if(S.empty()){
			//要么有环 要么处理完毕 
			break; 
		} 
		int cur=S.top();
		S.pop();
		cout<<"将"<<G.vexs[cur]<<"放入结果集中"<<endl; 
		result.push_back(G.vexs[cur]);
		//同时需要将count处理的，下面处理count数组
		count[cur]=-1; 
		for(int j=0;j<G.vexnum;j++){
			if(G.arcs[cur][j]){
				count[j]-=1;
				G.arcs[cur][j]=0;
			}
			if(count[j]==0){
				cout<<"将"<<G.vexs[j]<<"放入栈集中"<<endl;
				S.push(j);
			}
		} 	
	}
	if(result.size()==G.vexnum){
		for(int i=0;i<G.vexnum;i++){
			cout<<result[i]<<" ";
		}
		cout<<endl;
	}
	else cout<<"此时存在环"<<endl;
}

6.2.2、运行结果

用的测试图是上文中的三个测试图
第一个的输入方式

第二个的输入的方式与第一个一样 这里太长 就直接放结果吧

第三个测试图

七、可执行代码汇总

#include
using namespace std;
#define MaxInt 32767  //表示极大值∞  其实就是一种无穷标志
#define MVNum  100    //表示最大顶点数 
typedef char VerTexType;//假设顶点的数据结构类型为char 
typedef int  ArcType;//假设权值类型为整形
//下面的是邻接矩阵的 
typedef struct{
	 VerTexType vexs[MVNum];//顶点表 
	 ArcType  arcs[MVNum][MVNum];//邻接矩阵 
	 int vexnum;//图的当前顶点数
	 int arcnum;//图的当前边数
}AMGraph;
//创建一个无向图 ，其实就是填充两个数组 
void CreateAdjoin(AMGraph &G){
	cout<<"请输入顶点数和边数"<<endl;
	cin>>G.vexnum>>G.arcnum; 
	cout<<"请输入各个顶点名称"<<endl; 
	for(int i=0;i<G.vexnum;i++){
		cin>>G.vexs[i]; 
	}
	for(int h=0;h<G.arcnum;h++){
		char vex1;char vex2;
		cout<<"请输入弧的两个顶点(类如从A指向B则输入AB)"<<endl;
		cin>>vex1>>vex2;
		//首先来看是否存在这两个顶点  若是存在则找到这两个点对应的下标
		// 当然创建的时候一种更加简单的方式就是遍历二维数组 一个一个输入
		int i=0;while(G.vexs[i++]!=vex1);
		int j=0;while(G.vexs[j++]!=vex2);
		if(i>G.vexnum||j>G.vexnum){//没有找到 
			cout<<"你输入的结点值不正确"<<endl; 
		}
		else{
			cout<<"请输入此边对应的权重"<<endl; 
			cin>>G.arcs[i-1][j-1];
			//G.arcs[j-1][i-1]=G.arcs[i-1][j-1];
		}
	}
} 
void TopologicalSort1(AMGraph &G){
	int count[G.vexnum]={0};
	//初始状每一个结点的入度 也就是计算出count数组
	//通过计算邻接矩阵中每一列 来统计入度 
	for(int i=0;i<G.vexnum;i++){
		for(int j=0;j<G.vexnum;j++){
			if(G.arcs[j][i])count[i]++;
		} 
	} 
	//从中选择一个入度为零的 
	int i=0; vector<char> V;
	for(int x=0;x<G.vexnum;x++){//表示要循环的次数 
	 	int i=0; 
		while(count[i++]!=0);
		if(i>G.vexnum){//说明没有找到的 此时就要退出了  但是还需要判断是因为环才退出的 还是遍历完成 
			cout<<"存在环"<<endl; 
			return;
		} 
		else{//找到待删除的点  将其count置为-1 并将其关联的count数目减一 
			count[i-1]=-1;//-1是作为一种标记
			cout<<"将"<<G.vexs[i-1]<<"加入到容器中"<<endl; 
			V.push_back(G.vexs[i-1]); 
			for(int j=0;j<G.vexnum;j++){
				if(G.arcs[i-1][j]){//若是存在边，则将边删除 并处理count数组 
					//G.arcs[i-1][j]=0;
					count[j]-=1; 
				}
			} 
		} 
		cout<<"此时的count数组是"<<endl; 
		for(int H=0;H<G.vexnum;H++){
			cout<<count[H]<<" "; 
		}
		cout<<endl;
	}
		for(int i=0;i<G.vexnum;i++){
			cout<<V[i]<<" ";
		}
		cout<<endl;
}
void TopologicalSort2(AMGraph &G){
	int count[G.vexnum]={0};
	vector<char> result;//用来存放结果 
	stack<int> S;//定义一个栈 其中存放count值为零的角标 
	//初始状每一个结点的入度 也就是计算出count数组
	//通过计算邻接矩阵中每一列 来统计入度 
	for(int i=0;i<G.vexnum;i++){
		for(int j=0;j<G.vexnum;j++){
			if(G.arcs[j][i])count[i]++;
		} 
	} 
	//将可以此时count==0的结点 也就是可以遍历的放入栈中 
	for(int i=0;i<G.vexnum;i++){
		if(0==count[i]){
			cout<<"将"<<G.vexs[i]<<"放入栈中"<<endl; 
			S.push(i);
		}
	} 
	for(int h=0;h<G.vexnum;h++){//n个结点需要执行n次 
		if(S.empty()){
			//要么有环 要么处理完毕 
			break; 
		} 
		int cur=S.top();
		S.pop();
		cout<<"将"<<G.vexs[cur]<<"放入结果集中"<<endl; 
		result.push_back(G.vexs[cur]);
		//同时需要将count处理的，下面处理count数组
		count[cur]=-1; 
		for(int j=0;j<G.vexnum;j++){
			if(G.arcs[cur][j]){
				count[j]-=1;
				G.arcs[cur][j]=0;
			}
			if(count[j]==0){
				cout<<"将"<<G.vexs[j]<<"放入栈集中"<<endl;
				S.push(j);
			}
		} 	
	}
	if(result.size()==G.vexnum){
		for(int i=0;i<G.vexnum;i++){
			cout<<result[i]<<" ";
		}
		cout<<endl;
	}
	else cout<<"此时存在环"<<endl;
}
int main(){
	int choice;
	AMGraph G;
	CreateAdjoin(G);
	cout<<"请选择方式1还是方式2"<<endl;
	cin>>choice;
	switch(choice){
		case 1:{
			TopologicalSort1(G);
			break;
		}
		case 2:{
			TopologicalSort2(G);
			break;
		}
		default:{
			cout<<"你输入的不正确"<<endl; 
			break;
		}
	} 
	
}

总结

其实代码也还好，不难有兴趣的可以尝试一下 反正我确实是一遍打出来了 感觉不错点个赞呗，你都点赞是对作者莫大的鼓舞