机器学习之主成分分析PCA原理及python实现
参考链接:PCA的数学原理
参考链接: 使用numpy来理解PCA和SVD
文章目录
- 前言
- 一、PCA的原理及优化目标
-
- 1.什么是投影?
- 2.如何进行投影?
- 3. 如何刻画投影值尽可能分散?
- 二、[PCA的数学原理](http://blog.codinglabs.org/articles/pca-tutorial.html)中的PCA实例python实现
- 三、调用sklean中的PCA验证PCA,鸢尾花数据集进行验证
- 总结
-
- 纸上得来终觉浅,绝知此事要躬行。
前言
众所周知,很多机器学习算法的复杂度和数据的维数有着密切关系,甚至与维数呈指数级关联。实际机器学习中处理成千上万甚至几十万维的情况也并不罕见,在这种情况下,机器学习的资源消耗是不可接受的,因此我们必须对数据进行降维。降维技术分为有监督和无监督的方式,今天分享下我对无监督降维PCA的理解,如有不妥,请为之指正。
一、PCA的原理及优化目标
PCA是主成分分析的缩写,目的是找到数据中的一些主要成分,而舍弃掉一部分无用的信息?那是怎么才能知道哪些是无用的信息?先来看一下PCA是怎么做的:PCA的基本思想是将原始的特征数据投影到某些方向上,使得投影值尽可能的分散,就可以保留保留了最大的信息。用二维数据降到一维来说就是将二维数据投影到一维度上,其投影值尽可能的分散,这样一维的数据就可能最大的表示二维数据。因此就需要取刻画这些问题:
- 什么是投影?
- 如何进行投影?
- 如何刻画投影值尽可能分散?
因此,先进行解释下上面的问题。
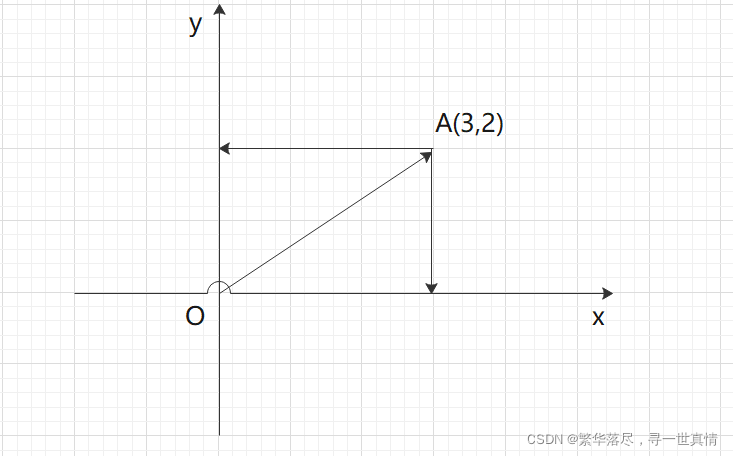
1.什么是投影?
如上图A这一点,(3,2)就表示OA向量在x轴上的投影为4,在y轴上的投影为2。
2.如何进行投影?
其中隐藏了一个隐含变量,就是基,默认笛卡尔坐标系的基为(1,0),(0,1),因此向量OA的线性形式可以表示为:

假如向量的的坐标系变为x1oy1,那么x1oy1的基就变成根号2分之1,在新基下A的坐标为:


一般的,如果我们有M个N维向量,想将其变换为由R个N维向量表示的新空间中,那么首先将R个基按行组成矩阵A,然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果,其中AB的第m列为A中第m列变换后的结果。

最后,上述分析同时给矩阵相乘找到了一种物理解释:
两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中每一行行向量为基所表示的空间中去。
3. 如何刻画投影值尽可能分散?
采用PCA的数学原理中的例子进行刻画,参照:协方差矩阵及优化目标→方差→协方差→协方差矩阵→协方差矩阵对角化阅读,PCA算法的流程为:
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X,即对原始进行转置
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵C=1/mXXT**(m为样本的个数,即n)**
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据,(注意X为0均值化,不是原始数据)
二、PCA的数学原理中的PCA实例python实现
PCA算法代码如下:
# -*- coding:utf-8 -*-
import numpy as np
"""
# 原文链接:http://blog.codinglabs.org/articles/pca-tutorial.html
PCA算法的计算流程:
设有m条n维得数据
1.将原始数据按列组成n行m列矩阵x,(即对原始进行转置)
2.将x的每一行进行零均值化
3.求出协方差均值C=1/mXXT(m为样本的属性,即n)
4.求协方差矩阵的特征值及对应的特征向量
5.将特征向量按对应的特征值大小从上到下排列成矩阵,取k行组成投影矩阵
6.Y=PX即为降维到k为的数据,(X为0均值化,不是原始数据)
"""
def mypca(x,n):
"""
函数的功能:传入原始数据矩阵x和最终维度的n,返回投影矩阵p
"""
# 2.将x的每一行进行零均值化
# 按列进行求均值
x = x.T
x_ = x.mean(axis=1)
# 按列均值后维度会降低,因此需要升维操作
x_ = np.expand_dims(x_, axis=1)
x = x - x_
#print(x)
#[[-1. -1. 0. 2. 0.]
# [-2. 0. 0. 1. 1.]]
# 3.求出协方差均值C=1/mXXT
c = 1/(x.shape[1])*np.dot(x,x.T)
#print(c)
#[[1.2 0.8]
# [0.8 1.2]]
# 4.求协方差矩阵的特征值及对应的特征向量
eig_values,eig_vocter = np.linalg.eig(c)
#print(eig_values)
#[2. 0.4]
#print(eig_vocter)
#[[ 0.70710678 -0.70710678]
# [ 0.70710678 0.70710678]]
# 5.将特征向量按对应的特征值大小从上到下排列成矩阵,取k行组成投影矩阵
sort_index = np.argsort(eig_values)[::-1]
p = eig_vocter[:,sort_index[0:n]]
#print(p)
#[0.70710678, 0.70710678]
return p.T,x
if __name__ == "__main__":
# 5条数据
x1 = [1,1]
x2 = [1,3]
x3 = [2,3]
x4 = [4,4]
x5 = [2,4]
# 1.将原始数据按列组成n行m列矩阵x
x = np.array([x1,x2,x3,x4,x5])
p,xxx = mypca(x,1)
x_new = np.dot(p,xxx)
# [[-2.12132034 -0.70710678 0. 2.12132034 0.70710678]]
# 为了迎合sklean处理数据的返回格式,需要进行转置
print(x_new.T)
#[[-2.12132034]
#[-0.70710678]
#[ 0. ]
#[ 2.12132034]
#[ 0.70710678]]
三、调用sklean中的PCA验证PCA,鸢尾花数据集进行验证
# -*- coding:utf-8 -*-
import numpy as np
from sklearn.decomposition import PCA
"""
# 原文链接:http://blog.codinglabs.org/articles/pca-tutorial.html
PCA算法的计算流程:
设有m条n维得数据
1.将原始数据按列组成n行m列矩阵x,(即对原始进行转置)
2.将x的每一行进行零均值化
3.求出协方差均值C=1/mXXT(m为样本的属性,即n)
4.求协方差矩阵的特征值及对应的特征向量
5.将特征向量按对应的特征值大小从上到下排列成矩阵,取k行组成投影矩阵
6.Y=PX即为降维到k为的数据,(X为0均值化,不是原始数据)
"""
def mypca(x,n):
"""
函数的功能:传入原始数据矩阵x和最终维度的n,返回投影矩阵p
"""
# 2.将x的每一行进行零均值化
# 按列进行求均值
x = x.T
x_ = x.mean(axis=1)
# 按列均值后维度会降低,因此需要升维操作
x_ = np.expand_dims(x_, axis=1)
x = x - x_
#print(x)
#[[-1. -1. 0. 2. 0.]
# [-2. 0. 0. 1. 1.]]
# 3.求出协方差均值C=1/mXXT
c = 1/(x.shape[1])*np.dot(x,x.T)
#print(c)
#[[1.2 0.8]
# [0.8 1.2]]
# 4.求协方差矩阵的特征值及对应的特征向量
eig_values,eig_vocter = np.linalg.eig(c)
#print(eig_values)
#[2. 0.4]
#print(eig_vocter)
#[[ 0.70710678 -0.70710678]
# [ 0.70710678 0.70710678]]
# 5.将特征向量按对应的特征值大小从上到下排列成矩阵,取k行组成投影矩阵
sort_index = np.argsort(eig_values)[::-1]
p = eig_vocter[:,sort_index[0:n]]
#print(p)
#[0.70710678, 0.70710678]
return p.T,x
if __name__ == "__main__":
# 5条数据
x1 = [1,1]
x2 = [1,3]
x3 = [2,3]
x4 = [4,4]
x5 = [2,4]
# 1.将原始数据按列组成n行m列矩阵x
x = np.array([x1,x2,x3,x4,x5])
p,xxx = mypca(x,1)
x_new = np.dot(p,xxx)
# [[-2.12132034 -0.70710678 0. 2.12132034 0.70710678]]
# 为了迎合sklean处理数据的返回格式,需要进行转置
print(x_new.T)
#[[-2.12132034]
#[-0.70710678]
#[ 0. ]
#[ 2.12132034]
#[ 0.70710678]]
# 调用sklean中的pca,验证结果
pca111 = PCA(n_components=1)
newx = pca111.fit_transform(x)
print(newx)
#[[ 2.12132034]
# [ 0.70710678]
# [-0. ]
# [-2.12132034]
# [-0.70710678]]
# 读取鸢尾花的数据,进行降维
import pandas as pd
pf = pd.read_csv("iris.csv")
x1 = pf[['150', '4', 'setosa', 'versicolor']].values
p,xxx1 = mypca(x1,2)
x1_new = np.dot(p,xxx1)
# 为了迎合sklean处理数据的返回格式, 需要进行转置
print(x1_new.T[:5,:])
print("----------------------")
pca111 = PCA(n_components=2)
newx = pca111.fit_transform(x1)
print(newx[:5,:])
[[-2.12132034]
[-0.70710678]
[ 0. ]
[ 2.12132034]
[ 0.70710678]]
[[ 2.12132034]
[ 0.70710678]
[-0. ]
[-2.12132034]
[-0.70710678]]
[[-2.68412563 -0.31939725]
[-2.71414169 0.17700123]
[-2.88899057 0.14494943]
[-2.74534286 0.31829898]
[-2.72871654 -0.32675451]]
----------------------
[[-2.68412563 0.31939725]
[-2.71414169 -0.17700123]
[-2.88899057 -0.14494943]
[-2.74534286 -0.31829898]
[-2.72871654 0.32675451]]
通过观察结果,只是有些结果的负号发生了变化,但是降维后的数值是一样的。这是为什么?这是因为sklean中采用的是奇异值分解SVD进行解PCA(目的是提升效率),但是奇异值分解的结果是唯一的,但是分解出来的U矩阵和V矩阵的正负可以不是唯一,只要保证它们乘起来是一致的就行。这就是出现负号不一致的的原因。详细参考:使用numpy来理解PCA和SVD
总结
PCA算法是一个非监督学习的降维方法,它只需要特征值分解,就可以对数据进行压缩,去噪。因此在实际场景应用很广泛。
PCA算法的主要优点有:
1)仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
2)各主成分之间正交,可消除原始数据成分间的相互影响的因素。
3)计算方法简单,主要运算是特征值分解,易于实现。
PCA算法的主要缺点有:
1)主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
2)方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
纸上得来终觉浅,绝知此事要躬行。
往期回归
机器学习之感知机算法原理及python实现