【目标检测】SPP-Net

概述

过往的基于CNN的网络都会通过裁剪的缩放将输入图片的尺寸固定，这样的话其实是会降低模型对于任意大小和任意比例图片的检测能力的，前者可能无法完全包含目标。

那么为什么网络会需要固定尺寸的输入呢？主要是由于全连接层的特性决定的。因为卷积可以看做是滑窗的形式，而池化可以看做是一种卷积的特例，对于他们而言任意的输入都可以得到对应的输出。全连接层就不一样了，输入和输出的神经元个数是固定的，那么它前一层输出的特征图就应该是固定尺寸的。

SPP-Net提出了一种Spatial Pyramid Pooling （SPP）的池化方式，代替了最后一次的池化操作，使得对于任意的输入都可以得到固定的输出，那也就满足了后面全连接层的要求了。

优势：：1、对于任意的输入，都可以得到固定的输出，这是以往的DCNN做不到的；2、SPP相当于是多尺度池化，让模型的鲁棒性更强；3、可以进行多尺度训练，提高模型的泛化能力，减低过拟合

细节

网络结构

其实spp这种思想很早就有，可以看做是词袋模型的泛化，过往很多模型都用过（DPM)、Overfeat），但是SPP-Net是第一个将这种思想用到DCNN中的。

他与传统的网络结构比较如下：因为全连接层的存在，给到全连接层的向量维度的固定的，传统的网络一开始就做好了准备（裁剪、缩放），而SPP-Net将最后的一个池化层转换成SPP模块，达到了要求。

SPP

前面说了，网络允许任意大小的输入，所以这个黑色部分表示的卷积层结果可以是任意大小的，假设他是$n\ast n\ast 256$的三维向量，接着我们将它划分为若干个网格，对于每一个网格进行池化（类似全局平均池化，只会得到一个特征），假设划分方式为$4\ast 4$、$2\ast 2$、$1\ast 1$，池化方式不论，我们就能分别得到$(4\ast 4+2\ast 2+1\ast 1)$个$1\ast 1\ast 256$的三维向量（因为池化只改变尺寸不改变通道数），接着把他们拼起来就可以得到一个$1\ast 21\ast 256$的三维向量，展平之后就是一个$1\ast 21\ast 256$的一维向量，给到全连接层。

网络训练

论文中将网络的训练分为两种：一种是single-size,一种是Multi-size。
single-size训练：理论上我们可以直接以多尺度的原始图片作为输入，来训练网络，但是实际上，为了计算的方便，GPU,CUDA等比较适合固定尺寸的输入，所以训练的时候输入是固定了尺度了的$224\ast 224$，这是通过裁剪、缩放得到的。

Multi-size训练：使用两个尺度进行训练：$224\ast 224和180\ast 180$，后者是前者缩放得到的。训练时采用迭代，即用224的图片训练一个epoch，之后180的图片训练一个epoch，交替地进行。

SPP进行目标检测

对于R-CNN，算法过程是：

1. 在原图上进行选择性搜索，获得2000个候选框
2. 将每个候选框进行缩放，通过网络进行特征提取
3. 每个候选框对应一个特征，借助这些特征，通过SVM进行分类，通过NMS剔除部分候选框，最后通过一个bbox回归器对比原始候选框进行微调

这个流程一个很大的问题就是每个候选框都需要进行特征提取，带来了很大的计算冗余。

而对于SPP-Net而言，主要的区别就在第二点上，其余的操作是一样的。
这边是直接对整张图像进行特征提取，然后在得到的特征图上找到候选框对应的区域，接着对每个区域进行空间金字塔池化，得到固定长度的向量，交给全连接层。

在得到的特征图上找到候选框对应的区域？首先候选框,经过多层卷积之后，位置还是相对于原图不变的，如下图所示；至于具体的映射关系，看论文吧。

这一步的前半部分，应该是不难想到，就相当于是把划候选框的操作往后挪了，特征提取只需要做一次，大大减小了计算量，但是后面一步SPP才是精髓，没有这一步的话，不同尺寸的特征图，即使展平，得到的维度也是不同的，无法通过统一的全连接层处理，那也就代表了无法处理。

SPPLayer实现

因为spp中需要多级池化，如文中池化到$4\ast 4$、$2\ast 2$、$1\ast 1$的尺寸，或者说将特征图划分为$4\ast 4$、$2\ast 2$、$1\ast 1$的块，每个块采用类似于全局平均池化的方式得到一个特征。总之就需要多个池化，每个池化的具体参数需要根据输入的尺寸而定，相关公式如下所示。

相关公式：这是池化过程中设计的参数，上面是核的高、步长的高和padding的高，下面都是宽，n指的是需要需要池化到的长度。

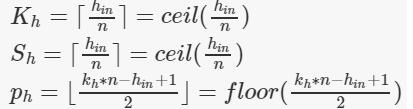
参考了网上的代码，但是和我理解的有点出入，我就稍微改了一点点

import paddle
import paddle.nn as nn
import math

# 构建SPP层(空间金字塔池化层)
# 核心就是对特征图进行多尺度池化（类似于全局平均池化），得到长度固定的一维向量
class SPPLayer(nn.Layer):
    # target_sizes就是希望池化到的尺寸，论文中是1x1 2x2 3x3
    def __init__(self, target_sizes, pool_type='max_pool'):
        super(SPPLayer, self).__init__()

        self.target_sizes = target_sizes
        self.pool_type = pool_type

    def forward(self, x):
        n, c, h, w = x.shape
        # 对特征图多次池化
        for idx,target_size in enumerate(self.target_sizes):
            # 计算池化的三个参数
            kernel_size = (math.ceil(h / target_size), math.ceil(w / target_size))
            stride = (math.ceil(h / target_size), math.ceil(w / target_size))
            padding = (math.floor((kernel_size[0]*target_size-h+1)/2), math.floor((kernel_size[1]*target_size-w+1)/2))

            # 声明池化方法
            max_pool = nn.MaxPool2D(kernel_size=kernel_size,stride=stride,padding=padding)
            print(max_pool(x).shape)
            if (idx == 0):
                # 池化、展平
                x_flatten = paddle.flatten(max_pool(x),1)
            else:
                # 池化、展平与拼接
                x_flatten = paddle.concat((x_flatten, paddle.flatten(max_pool(x),1)), 1)
        return x_flatten

def main():
    target_sizes=[1,2,4]
    x=paddle.randn((1,10,24,24))
    spp=SPPLayer(target_sizes)
    print(spp(x).shape)


if __name__ == '__main__':
    main()

结果：可以看到 池化后的shape是和我们设想的一样的，拼接的结果也没有问题