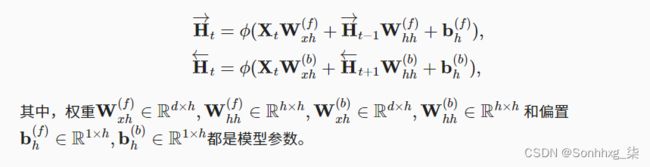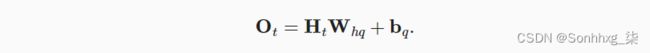【Pytorch深度学习实战】（8）双向循环神经网络（BiRNN）

 大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流

个人主页－Sonhhxg_柒的博客_CSDN博客 

欢迎各位→点赞 + 收藏⭐️ + 留言​

系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟

在序列学习中，我们以往假设的目标是： 在给定观测的情况下 （例如，在时间序列的上下文中或在语言模型的上下文中）， 对下一个输出进行建模。 虽然这是一个典型情景，但不是唯一的。 还可能发生什么其它的情况呢？ 我们考虑以下三个在文本序列中填空的任务：

• 我___。

• 我___饿了。

• 我___饿了，我可以吃半头猪。

根据可获得的信息量，我们可以用不同的词填空， 如“很高兴”（”happy”）、“不”（”not”）和“非常”（”very”）。 很明显，每个短语的“下文”传达了重要信息（如果有的话）， 而这些信息关乎到选择哪个词来填空， 所以无法利用这一点的序列模型将在相关任务上表现不佳。 例如，如果要做好命名实体识别 （例如，识别“Green”指的是“格林先生”还是绿色）， 不同长度的上下文范围重要性是相同的。 为了获得一些解决问题的灵感，让我们先迂回到概率图模型。

双向模型

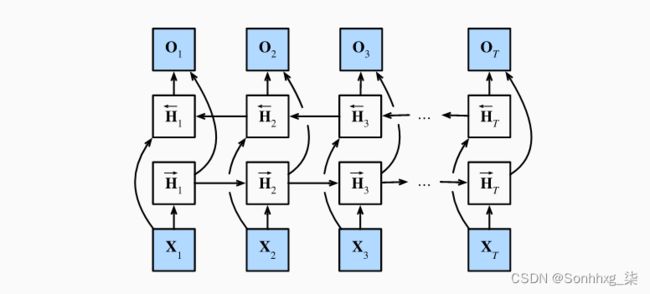
如果我们希望在循环神经网络中拥有一种机制， 使之能够提供与隐马尔可夫模型类似的前瞻能力， 我们就需要修改循环神经网络的设计。 幸运的是，这在概念上很容易， 只需要增加一个“从最后一个词元开始从后向前运行”的循环神经网络， 而不是只有一个在前向模式下“从第一个词元开始运行”的循环神经网络。 双向循环神经网络（bidirectional RNNs） 添加了反向传递信息的隐藏层，以便更灵活地处理此类信息。描述了具有单个隐藏层的双向循环神经网络的架构。

                                                  双向循环神经网络架构

事实上，这与隐马尔可夫模型中的动态规划的前向和后向递归没有太大区别。 其主要区别是，在隐马尔可夫模型中的方程具有特定的统计意义。 双向循环神经网络没有这样容易理解的解释， 我们只能把它们当作通用的、可学习的函数。 这种转变集中体现了现代深度网络的设计原则： 首先使用经典统计模型的函数依赖类型，然后将其参数化为通用形式。

1. 定义

双向循环神经网络是由 [Schuster & Paliwal, 1997]提出的， 关于各种架构的详细讨论请参阅 [Graves & Schmidhuber, 2005]。 让我们看看这样一个网络的细节。

对于任意时间步t，给定一个小批量的输入数据 Xt∈Rn×d （样本数：n，每个示例中的输入数：d）， 并且令隐藏层激活函数为ϕ。 在双向架构中，我们设该时间步的前向和反向隐状态分别为 H→t∈Rn×h和 H←t∈Rn×h， 其中h是隐藏单元的数目。 前向和反向隐状态的更新如下：

接下来，将前向隐状态H→t 和反向隐状态H←t连接起来， 获得需要送入输出层的隐状态Ht∈Rn×2h。 在具有多个隐藏层的深度双向循环神经网络中， 该信息作为输入传递到下一个双向层。 最后，输出层计算得到的输出为 Ot∈Rn×q（q是输出单元的数目）：

这里，权重矩阵Whq∈R2h×q 和偏置bq∈R1×q 是输出层的模型参数。 事实上，这两个方向可以拥有不同数量的隐藏单元。

2. 模型的计算代价及其应用

双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。 也就是说，我们使用来自过去和未来的观测信息来预测当前的观测。 但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的。 因为在预测下一个词元时，我们终究无法知道下一个词元的下文是什么， 所以将不会得到很好的精度。 具体地说，在训练期间，我们能够利用过去和未来的数据来估计现在空缺的词； 而在测试期间，我们只有过去的数据，因此精度将会很差。 下面的实验将说明这一点。

另一个严重问题是，双向循环神经网络的计算速度非常慢。 其主要原因是网络的前向传播需要在双向层中进行前向和后向递归， 并且网络的反向传播还依赖于前向传播的结果。 因此，梯度求解将有一个非常长的链。

双向层的使用在实践中非常少，并且仅仅应用于部分场合。 例如，填充缺失的单词、词元注释（例如，用于命名实体识别） 以及作为序列处理流水线中的一个步骤对序列进行编码（例如，用于机器翻译）。 

双向循环神经网络Pytorch的实现

import torch 
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms


# 设备配置
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

# 超参数
sequence_length = 28
input_size = 28
hidden_size = 128
num_layers = 2
num_classes = 10
batch_size = 100
num_epochs = 2
learning_rate = 0.003

# MNIST 数据集
train_dataset = torchvision.datasets.MNIST(root='../../data/',
                                           train=True, 
                                           transform=transforms.ToTensor(),
                                           download=True)

test_dataset = torchvision.datasets.MNIST(root='../../data/',
                                          train=False, 
                                          transform=transforms.ToTensor())

# 数据加载器
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                           batch_size=batch_size, 
                                           shuffle=True)

test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
                                          batch_size=batch_size, 
                                          shuffle=False)

# 双向循环神经网络（多对一）
class BiRNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, num_classes):
        super(BiRNN, self).__init__()
        self.hidden_size = hidden_size
        self.num_layers = num_layers
        self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True, bidirectional=True)
        self.fc = nn.Linear(hidden_size*2, num_classes)  # 2 for bidirection
    
    def forward(self, x):
        # 设置初始状态
        h0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device) # 2 for bidirection 
        c0 = torch.zeros(self.num_layers*2, x.size(0), self.hidden_size).to(device)
        
        # 前向传播 LSTM
        out, _ = self.lstm(x, (h0, c0))  # out: tensor of shape (batch_size, seq_length, hidden_size*2)
        
        # 解码上一个时间步的隐藏状态
        out = self.fc(out[:, -1, :])
        return out

model = BiRNN(input_size, hidden_size, num_layers, num_classes).to(device)


# 损失和优化器
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
    
# 训练模型
total_step = len(train_loader)
for epoch in range(num_epochs):
    for i, (images, labels) in enumerate(train_loader):
        images = images.reshape(-1, sequence_length, input_size).to(device)
        labels = labels.to(device)
        
        # 前向传播
        outputs = model(images)
        loss = criterion(outputs, labels)
        
        # 向后优化
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        if (i+1) % 100 == 0:
            print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}' 
                   .format(epoch+1, num_epochs, i+1, total_step, loss.item()))

# 测试模型
with torch.no_grad():
    correct = 0
    total = 0
    for images, labels in test_loader:
        images = images.reshape(-1, sequence_length, input_size).to(device)
        labels = labels.to(device)
        outputs = model(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

    print('Test Accuracy of the model on the 10000 test images: {} %'.format(100 * correct / total)) 

# 模型保存
torch.save(model.state_dict(), 'model.ckpt')