无人机群编队分析的定位问题 分析与思考-1(数学建模竞赛2022年B题)
2022年高教社杯全国大学生数学建模竞赛结束了,在此我们对 2022年 B题 进行一些分析与思考。
1. 初步印象
2022年 B题 (无人机遂行编队飞行中的纯方位无源定位)是一个有趣的题目。
随着无人机技术的快速发展,早已从高科技变做寻常物,成为同学科创选题,抖音街拍必备,少儿热门玩具,哦乌冲突达人。无人机集群的使用也越来越常见,频频现身于城市和高校庆典活动中,动辄数百架、数千架的编队都已屡见不鲜,只有表演失败失控炸机才能上头条。
严肃地说,无人机技术的军事用途潜力巨大,必将改变未来战争技术的形态和格局。本题的背景正是以军事用途的无人机编队定位问题为背景的:
(1)“遂行” 是什么意思?我望文生义以为是“随行”,某度搜索发现并没有这个意思,解释为“顺利通行”,请教专家说是军事术语。总是觉得有点别扭,所以我把题目简写为“无人机群编队飞行的定位问题”。
(2)“电磁静默”,这是典型的军事用途中的要求,民用无人机虽然有电磁干扰方面的要求,但跟“电磁静默”是两回事。
数模竞赛有多个题目,要从中选择一个完成。大家通常都会先把每个题目简单看一下,考虑选题后再仔细琢磨。当然很多同学在备赛时就会重点准备某类题型,奔着这类题目参赛的。但这次 B题似乎要别出心裁、打破常规了。
编队飞行,图 2 是圆形队形,图 3 是锥形队形。
首先想到的是规划问题,再看看却有点晕。线性规划,目标是什么?0-1规划,选择发射源?动态规划,选择路径?仔细看看都不像,套不上去。
拿到题目发现准备的题型算法套不上去,无从下手,怎么办?
方法一是果断放弃,方法二是多读几遍题目,仔细审题。
2. 仔细审题
题目只有一句话,你在选题时真的读懂了吗?
如果你还是选择 B题,那么我们还是一起再读读题目吧。
(1)“遂行编队”:什么意思,是一种特殊编队方式吗?没啥意思,就是编队飞行。
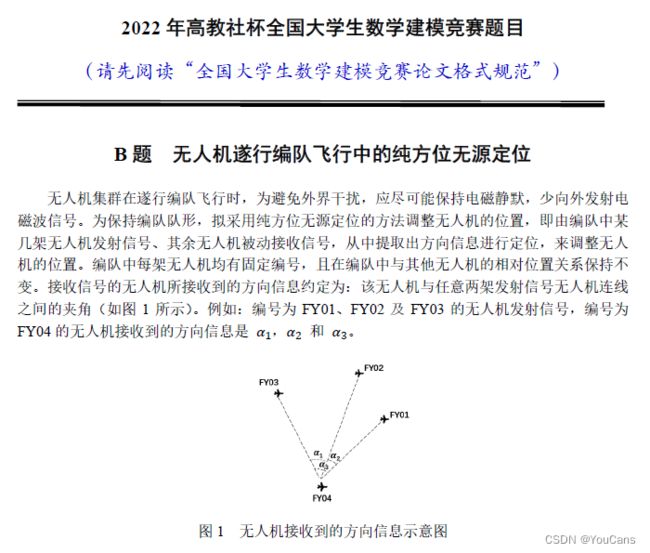
(2)“纯方位”:指只有方位数据,准确的说只有夹角方位,没有其它数据,特别是没有位置、距离、速度等空间数据可以使用。
(3)“无源定位”:
定位是明白的,无源呢?
某度百科说:无需能(电)源的器件就是无源器件;无源元件主要是电阻类、电感类和电容类元件,它的共同特点是在电路中无需加电源即可在有信号时工作。看懂了吗?
如果你再查查“无源信号”,会发现更加迷茫:无源信号是指没有电流输出的信号,比如开关信号。
看到这个题目,还很容易想到卫星定位,GPS/北斗系统,相关技术介绍和文献也很多。这个想法没有错,技术上也有很多关联性。但是如果你的思路和注意力聚焦于卫星定位,那么很遗憾,恐怕是误入歧途了。
要查的是“无源定位”!
- 无源定位技术由分开布置的几个侦察站共同完成,迅速确定雷达的位置。
- 无源雷达本身并不发射能量,而是被动地接收目标反射的非协同式辐射源的电磁信号,对目标进行跟踪和定位。所谓非协同式外部辐射源,是指辐射源和雷达“不搭界”,没有直接的协同作战关系。这样就使得探测设备和反辐射导弹不能利用电磁信号对无源雷达进行捕捉、跟踪和攻击。
- 因为无源侦察不能直接获得雷达所在的距离,所以无源定位要由分开布置的几个侦察站共同完成,或者由侦察站在运动过程中连续测量来实现。
- 多站定位主要有测向交叉定位、时差定位、多普勒差定位等几种。
成功密码是”测向交叉定位"!
如果你能查到“无源定位”这个词条,那么恭喜你,已经迈向成功的道路。如果你能进一步以”测向交叉定位"在某度和知网检索,那要更加恭喜你,已经成功了一半。当然,如果你愿意研究时差定位、多普勒差定位,也没有问题。
某度搜索结果:
-
测向交叉定位法(directional cosine intersection positioning method)是指利用测出3个方向图,即3个圆锥面,相交确定目标位置的方法。采用干涉仪测角原理,利用无线电波直线传播的特性,测量用户发射电磁波传播方向来测定用户相对于测站基线方向的夹角,基线两测站收到信号的相位差和基线的夹角成余弦关系,故称为方向余弦。
-
此方向余弦即代表测向。由两条基线测得测角的圆锥位置面而相交,即可得出和距离无关的目标在天球上的角位置,如有第三个基线测出第二个方向余弦,再定出第三个位置面,同前两个位置面相交于一点即可定出用户空间位置,即为测角交叉定位法。
-
无源定位方法分类:
(1)通过 2 个接收站测量目标信号的到达角,在二维或三维空间上经过射线交叉确定目标位置,这是测向交叉定位法。
(2)过多个接收站测量目标信号的到达时间,根据一个时间差确定一组双曲面,三组双曲面的公共点就是目标位置,这是时差定位法。(二维需要3个接收站,三维需要4个接收站)
(3)通过多个接收站测量目标信号的到达频率,一个多普勒频差可以确定一组椭球面,根据三组椭球面的公共点确定目标位置,这是差分多普勒定位法。(二维需要3个接收站,三维需要4个接收站) -
测向定位算法分类:
(1)利用包含目标坐标值的测量方程组来求解辐射源的位置信息,常用的是简化加权最小二乘定位算法;
(2)利用测量确定的定位线的空间几何关系确定辐射源的位置信息,例如以距离最短为准则的最小二乘-卡尔曼滤波算法、异面直线定位算法和垂线定位算法等 。
”测向交叉定位"知网检索结果有463篇文献,其中学术期刊330篇,学位论文121篇。例如:
- [1] 李鹏. 多目标测向定位跟踪技术研究[D].西安电子科技大学,2017.
- [2] 邹先雄. 无人机目标无源定位方法研究[D].电子科技大学,2018.
- [3] 何朝鑫. 对多运动辐射源的测向融合定位跟踪技术研究[D].国防科技大学,2019
- [4] 宗军君,崔逊学.多站测向交叉定位的加权最大似然估计算法及其精度分析[J].电光与控制,2015
- [5] 李鹏.基于改进的Hough变换的多目标无源测向交叉定位技术[J].舰船电子对抗,2017
- [6] 张志虎,赵佳旻,刘梅.测向交叉定位体制下平台航迹最优规划算法[J].指挥控制与仿真,2018
- [7] 田晗.多站测向交叉定位中的非线性改进最小二乘法[J].科技通报,2018
- [8]李洪科, 黄麟舒. 测向交叉定位方法在工程中的应用[J]. 舰船科学技术, 2013
- [9] 李万春. 一种基于角度信息的无源多站多目标测向交叉定位方法. 电子科技大学. CN201711337488.7
本发明属于电子对抗技术领域,涉及一种基于角度信息的无源多站多目标测向交叉定位方法.首先采用多辐射源数据关联算法,将多个观测站的观测数据进行关联得到代价矩阵C(p,q),再根据获得的代价矩阵C(p,q),采用k均值++聚类算法估计出目标坐标.本发明的有益效果为,本发明可以准确对多站数据完成关联,并最终准确估计出目标的位置,方法简单,效果良好.
3. 回顾与反思
现在再看看这个题目,看了以上解读,请问你是什么心情?沾沾自喜,恍然大悟,还是欲哭无泪?
以此为例,对看到本文的小伙伴们说一句:选择比努力更重要,多花一些时间审题、多读几遍题目,永远都是必要的。
这才哪里啊,只是赛题的标题而已,题目中藏着的几十项重要条件和提示,你看出来了吗,看懂了吗?请看明天的更新:无人机群编队分析的定位问题 分析与思考-2(数学建模竞赛2022年B题)。
接受读者建议,发起一个投票,大家过两天可以看看各位赛友的心情。呵呵。
【本节完】
『Python小白的数学建模课 @ Youcans』 版权声明:
youcans@xupt 原创作品,转载必须标注原文链接:(https://blog.csdn.net/youcans/article/details/126927831)
Copyright 2022 youcans
Crated:2022-9-19