【刷题日记】笔试经典编程题目（七）

大家好，我是白晨，一个不是很能熬夜，但是也想日更的人✈。如果喜欢这篇文章，点个赞，关注一下白晨吧！你的支持就是我最大的动力！

前言

---

虽然还有很多课，但是也不能忘了写编程题呀。

白晨总结了大厂笔试时所出的经典题目，本周题型包括动态规划，条件控制，回溯算法等，其中动态规划题目题目占了一半。这次的题目平均难度比和上一周的题目差不多，但是这周的动态规划和深度优先搜索都是非常经典的题目，如果以前没有做过，可能会卡住。

都是很有代表性的经典题目，适合大家复习和积累经验。

这里是第七周，大家可以自己先试着自己挑战一下，再来看解析哟！

笔试经典编程题目（七）

---

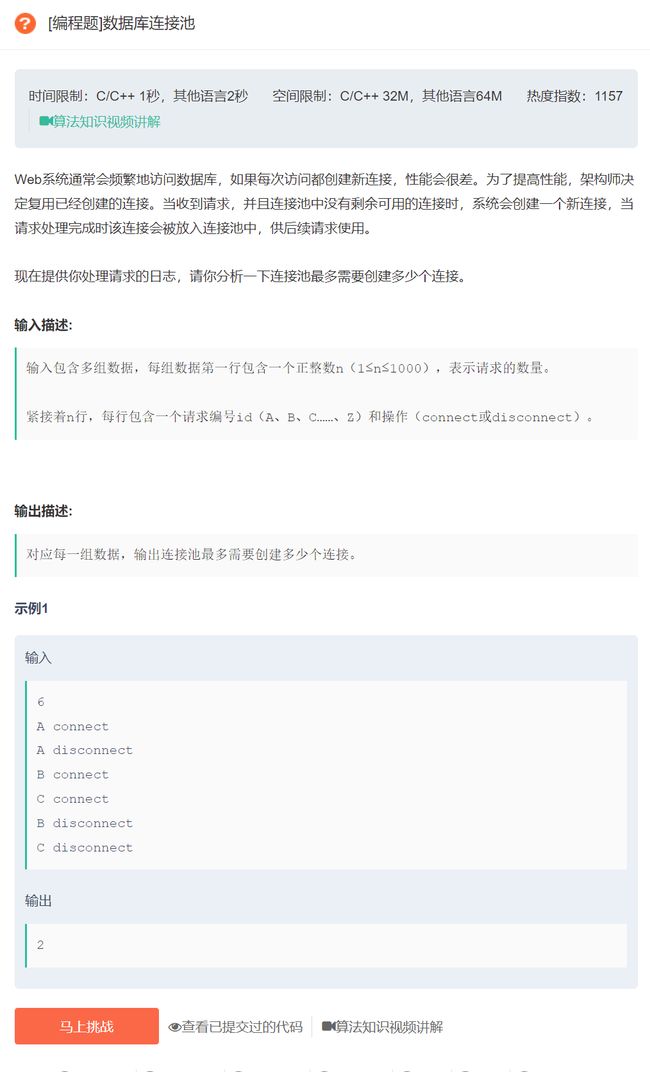
1.数据库连接池

---

原题链接：数据库连接池

算法思想：

• 这道题的意思就是让编号为A到Z的节点去连接数据库，当发出connect指令时，视为连接，发出disconnect指令时，视为断开连接。当connect指令发出，并且数据库中没有多余连接时，会创建一个连接，如果有多余连接，那么不会创建连接。并且，disconnect指令会断开发出这个指令节点的连接，但是会保留已有的连接。
• 拿图中例子举例：

1. A先发出connect指令，但是此时没有连接，创建一个连接，此时创建的连接数为1。
2. A发出disconnect指令，断开连接，但已创建的连接数不变，此时创建的连接数依然为1。
3. B发出connect指令，此时有空连接，不用创建，创建的连接数依然为1。
4. C发出connect指令，此时没有空连接，创建一个连接，此时创建的连接数为2。
5. B,C发出disconnect指令，断开连接，所以最终创建的连接数为2。

• 从上面例子可以得出：这道题就是问要至少创建多少个连接可以满足一组日志中同时的最大连接数量。
• 我们模拟栈来完成本题，cur为当前连接数，Max为最大连接数。
• 当cur小于等于Max时，继续遍历指令，当cur大于Max时，Max = cur。
• 最后求得Max就是同时最大的连接数量。

代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    int n;
    int cur = 0, Max = 0;
    while (cin >> n)
    {
        vector<char> id(n);
        vector<string> signal(n);
        for (int i = 0; i < n; ++i)
        {
            cin >> id[i];
            cin >> signal[i];
        }

        for (auto& s : signal)
        {
            if (s == "connect")
                cur++;
            else
                cur--;
            Max = max(Max, cur);
        }
        cout << Max << endl;
    }
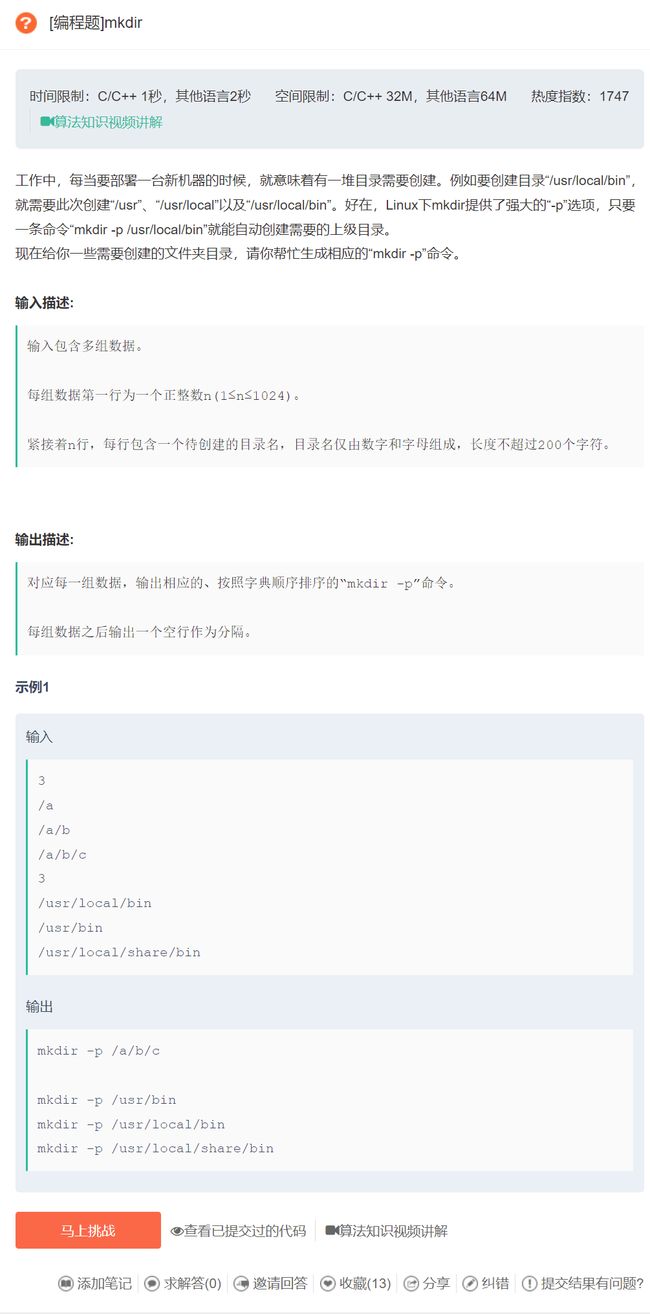
    return 0;
}

---

2.mkdir

---

原题链接：mkdir

算法思想：

• 这道题目就是考验控制能力的经典题目，其中的细节非常多，稍有不慎就会出错。

• 首先，可以按照升序将指令字符串排序，这样便于去重。

• 其次，对于指令进行遍历，比较前后两个字符串，判断要不要输出。

• 输出条件：满足条件一和条件二就可以将前面的字符串输出（输出条件其实就是为了判断后面指令不是在前面指令的基础上进一步的创建子目录，取消重复命令）

  • 条件一：这两个字符串不相等。
  • 条件二：满足下面条件任意一条即可。
    • 前面字符串的长度大于后面字符串的长度。
    • 后面字符串的子串（从下标为0到下标为前面字符串长度-1，也就是和前面字符串同样长的子串）不等于前面的字符串。
    • 虽然后面字符串的子串（从下标为0到下标为前面字符串长度-1，也就是和前面字符串同样长的子串）等于前面的字符串，但是后面字符串下标为前面字符串长度的字符不为/。举个例子：前面字符串：a/b/c，后面字符串：a/b/cd，这两个虽然后面的子串等于前面的字符串，但是这两个是不同的目录，需要分别输出。

• 最后，输出最后一条指令（这道指令是必然会输出的）。

代码实现：

#include 
#include 
#include 
#include 
using namespace std;

int main()
{
    int n;
    while (cin >> n)
    {
        vector<string> v(n);
        for (int i = 0; i < n; ++i)
            cin >> v[i];

        sort(v.begin(), v.end());
        
        for (int i = 0; i < n - 1; ++i)
        {
            // 满足条件一和条件二才可以输出
            if (v[i] != v[i + 1] &&
                (v[i + 1].size() < v[i].size() ||
                    v[i + 1].substr(0, v[i].size()) != v[i]
                    || v[i + 1][v[i].size()] != '/'))
                cout << "mkdir -p " << v[i] << endl;
        }
        cout << "mkdir -p " << v.back() << endl << endl;
    }
    return 0;
}

---

3.红与黑

---

原题链接：红与黑

算法思想：

• 这是一道非常典型的深度优先搜索的题目，没有什么特别的难的地方，如果没有见过类似题目的同学可以先看看【刷题日记】回溯算法(深度优先搜索)经典题目这篇文章。
• 直接从起点字符开始向四个方向暴力搜索，用一个bool数组判断是否已经访问此位置，一个引用传参num记录黑瓷砖的数量，如果没有访问，++num，将其标记为已访问，然后以这个位置为起点继续向四个方向搜索。
• 具体实现细节见代码：

代码实现：

#include 
#include 
using namespace std;
// 四个方向的坐标
static int des[4][2] = { {1,0},{-1,0},{0,1},{0,-1} };
void Dfs(vector<vector<char>>& vc, vector<vector<bool>>& vbool, int& num, int curX, int curY, int m, int n)
{
    // num记录黑瓷砖数量
	++num;
    // 标记为已访问
	vbool[curX][curY] = true;
	// 向上下左右四个方向分别进行访问
	for (int i = 0; i < 4; ++i)
	{
        // 算出新坐标
		int newX = curX + des[i][0];
		int newY = curY + des[i][1];
		// 如果新坐标越界，跳过此方向的访问
		if (newX < 0 || newX >= m || newY < 0 || newY >= n)
			continue;
		// 当新坐标对应的字符是.，并且未被访问，则进行访问
		if (vc[newX][newY] == '.' && vbool[newX][newY] == false)
			Dfs(vc, vbool, num, newX, newY, m, n);
	}
}

int main()
{
	int m, n;
	while (cin >> m >> n)
	{
		int beginX = 0, beginY = 0;
		int num = 0;
		vector<vector<char>> vc(m, vector<char>(n));
		vector<vector<bool>> vbool(m, vector<bool>(n, false));
		for (int i = 0; i < m; ++i)
		{
			for (int j = 0; j < n; ++j)
			{
				cin >> vc[i][j];
				if (vc[i][j] == '@')
				{
					beginX = i;
					beginY = j;
				}
			}
		}
		Dfs(vc, vbool, num, beginX, beginY, m, n);
		cout << num << endl;
	}
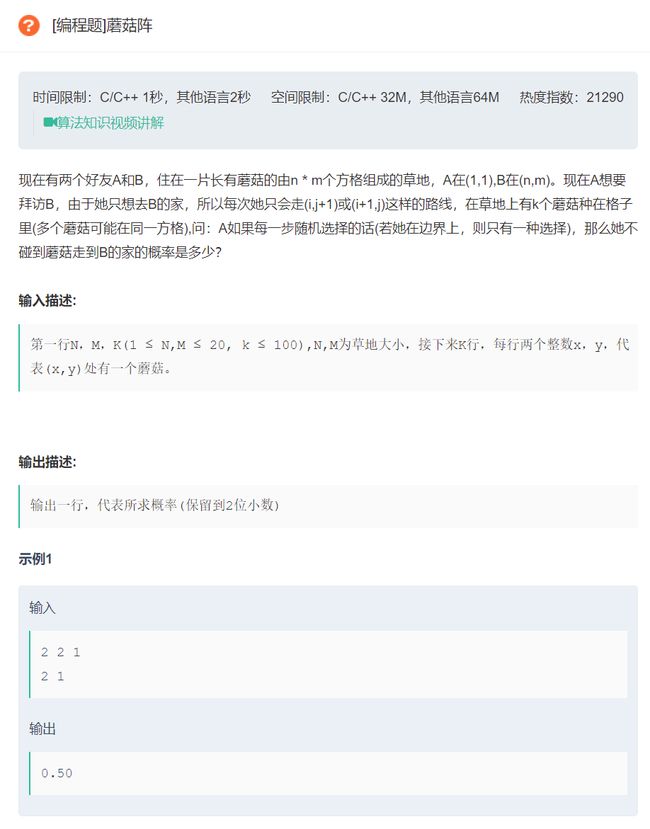
	return 0;
}

---

4.蘑菇阵

---

原题链接：蘑菇阵

算法思想：

• 这道题是一道动态规划的题目，但是不可以直接用 不遇到蘑菇的路径和/所有路径和 得到结果，因为每条路的概率是不同的，这是这道题比较坑的地方。

以上原因来自牛客网网友

• 这道题应该直接用概率求解，具体意思是每个位置记录到达此位置的概率。

• 状态：f(i,j) -- 到达此位置的概率

• 初始值：$f(1,1)=1$

• 状态转移方程：最重要的一点就是看从哪几个点可以到这个点

  • 一般情况，$(i,j)$可以从$(i-1,j)$和$(i,j-1)$走来，并且$(i-1,j)$可以走右或者走下，如果走下就走到$(i,j)$，所以概率是0.5，同理$(i,j-1)$走到$(i,j)$的概率也是0.5，所以

  $$f(i,j)=f(i-1,j)\ast 0.5+f(i,j-1)\ast 0.5$$

以下全部为特殊情况：

• 当 $i==1$​时，也就是第一行的点，此时只能从左边的点来，并且左边的点可能走下或者走右，所以
  KaTeX parse error: Can't use function '$' in math mode at position 23: … = 0.5*f(1,j-1)$̲​

• 当 $j==1$ 时，同上，
  $$f(i,1)=0.5\ast f(i-1,1)$$

• 当$i==m\&\&j==n$时，也就是终点，终点由可以从终点上面的点和终点左边的点来，并且这两个点都只能走终点这一个点，这个点就等于左边点的概率加上边点的概率，
  $$f(m,n)=f(m-1,n)+f(m,n-1)$$

• 当$i==m\&\&j\ne n$​时，也就是在最后一行时但不为终点时，这个点可能从上面或者左边来，左边的点必须走这个点，上边的点可以走下或者走右，所以
  $$f(m,j)=f(m-1,j)\ast 0.5+f(m,j-1)$$

• 当$i\ne m\&\&j==n$​时，也就是在最后一列时但不为终点时，这个点可能从上面或者左边来，上边的点必须走这个点，左边的点可以走下或者走右，所以
  $$f(i,n)=f(i,n-1)\ast 0.5+f(i-1,n)$$

• 当遇到蘑菇点时，
  $$f(i,j)=0$$

代码实现：

#include 
#include 
using namespace std;

int main()
{
	int m, n, k;
	while (cin >> m >> n >> k)
	{
		vector<vector<double>> dp(m + 1, vector<double>(n + 1));
		vector<vector<bool>> vbool(m + 1, vector<bool>(n + 1, false));
		int x, y;
		while (k--)
		{
			cin >> x >> y;
			vbool[x][y] = true;
		}

		for (int i = 1; i <= m; ++i)
		{
			for (int j = 1; j <= n; ++j)
			{
				if (i == 1 && j == 1)
					dp[i][j] = 1;
				else if (vbool[i][j])
					dp[i][j] = 0;
				else if (i == 1)
					dp[i][j] = m > 1 ? dp[i][j - 1] * 0.5 : dp[i][j - 1];
				else if (j == 1)
					dp[i][j] = n > 1 ? dp[i - 1][j] * 0.5 : dp[i][j - 1];
				else if (i == m && j == n)
					dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
				else if (i == m)
					dp[i][j] = dp[i][j - 1] + dp[i - 1][j] * 0.5;
				else if (j == n)
					dp[i][j] = dp[i - 1][j] + dp[i][j - 1] * 0.5;
				else
					dp[i][j] = dp[i - 1][j] * 0.5 + dp[i][j - 1] * 0.5;
			}
		}
		printf("%.2lf\n", dp[m][n]);
	}
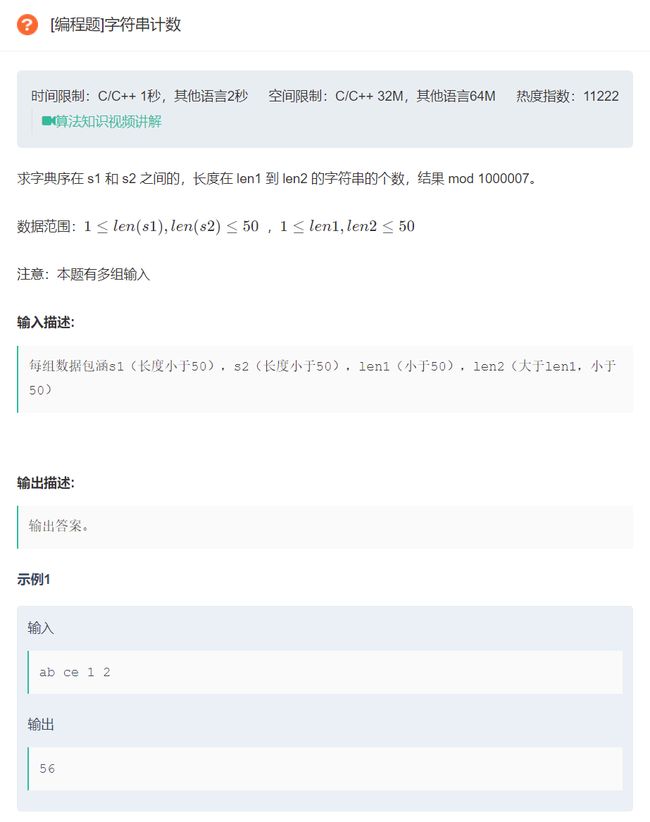
	return 0;
}

---

5.字符串计数

---

原题链接：字符串计数

算法思想：

• 首先，要了解什么是字典序。

设想一本英语字典里的单词，何者在前何者在后？

显然的做法是先按照第一个字母、以 a、b、c……z 的顺序排列；如果第一个字母一样，那么比较第二个、第三个乃至后面的字母。如果比到最后两个单词不一样长（比如，sigh 和 sight），那么把短者排在前。

通过这种方法，我们可以给本来不相关的单词强行规定出一个顺序。“单词”可以看作是“字母”的字符串。

• 其次，长度为len1到len2的字符串是，长度为len1的字符串，长度为len1+1的字符串，长度为len1+2的字符串，…，长度为len2的字符串。
• 再者，什么叫在字典序在s1和s2之间的字符串，长度在len1和len2之间的字符串？

我们以图中数据举例：

s1：ab ，s2：ce

len1：1 ，len2：2

• 长度为1的，字典序在s1和s2之间的字符串：b，c

  注意：a不是，因为a比s1短，比s1的字典序排名靠前。

• 长度为2的，字典序在s1和s2之间的字符串：ac，ad，ae，af，…，ba，bb，bc，…，ca，cb，cc，cd

  注意：

  • ab，ce不是，s1和s2之间可以理解为开区间(ab,ce)。
  • 通过观察，我们发现通过长度为1的字符串包含了长度为2为字符串的前缀，但是并不包含长度为2字符串的a前缀。

• 通过上面的例子我们可以得到：

  • 这是一道动态规划的变式题目，长度为n的字符串可以通过长度为n-1的字符串推得。我们以上面的例子举例：

  长度为2的字符串 = 长度为1的字符串 * 26 + ac到az - ce到cz

  • 当$n<=s1.size(),n<s2.size()$时，长度为n字符串 = 长度为n - 1的字符串 * 26 + s1[n - 1] + 1到z的字符数量 - s2[n-1] + 1到z的字符数量。
  • 当$n<=s2.size()$时，长度为n字符串 = 长度为n - 1的字符串 * 26 + s1[n - 1] + 1到z的字符数量 - s2[n-1]到z的字符数量。
  • 当$n>s1.size(),n>s2.size()，n-1\ne s1.size()$时，长度为n字符串 = 长度为n - 1的字符串 * 26 。
  • 当$n>s1.size(),n>s2.size()，n-1=s1.size()$时，长度为n字符串 = (长度为n - 1的字符串 + 1) * 26 。

• 具体实现见代码：

代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
	string s1, s2;
	int len1, len2;
	while (cin >> s1 >> s2 >> len1 >> len2)
	{
		// 从下标为1开始记录
		vector<int> v(len2 + 1, 0);
		int i = 0;
		// 跳过相等的元素
		while (s1[i] == s2[i])
			i++;
		if (s2.size() > i + 1)
			v[i + 1] = s2[i] - s1[i];
		else
			v[i + 1] = s2[i] - s1[i] - 1;
		// 遍历字符串，进行动规
		for (i = i + 2; i <= len2; ++i)
		{
			int cnt = 0;// 补全值
			if (i <= s1.size())
				cnt += 'z' - s1[i - 1];
			if (i < s2.size())
				cnt -= 'z' - s2[i - 1];
			if (i == s2.size())
				cnt -= 'z' - s2[i - 1] + 1;
			v[i] = (26 * v[i - 1]) % 1000007 + cnt;
		}
		int ans = 0;
		for (int j = len1; j <= len2; ++j)
		{
			ans += v[j];
			ans %= 1000007;
		}
		cout << ans << endl;
	}
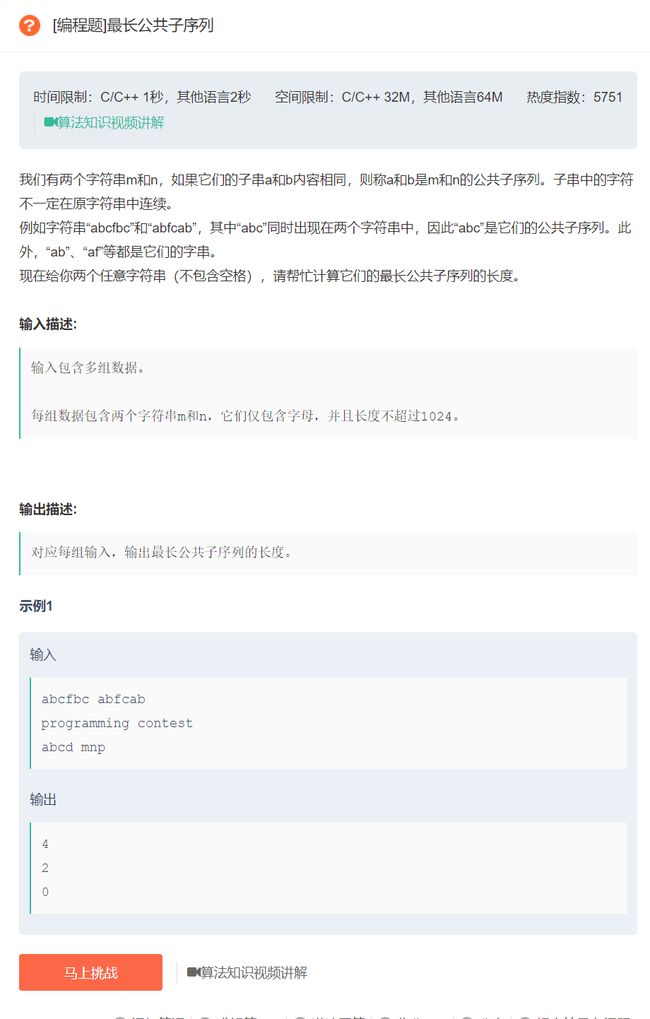
	return 0;
}

---

6.最长公共子序列

---

原题链接：最长公共子序列

算法思想：

• 这道题是一道非常经典的动态规划题目，实现的思路也比较简单。

• 状态：f(i,j) —— s1前i个字符和s2前j个字符最长公共序列。

• 初始值：$f(i,0)=f(0,j)=0$

• 状态转移方程：如果$s1[i-1]==s2[i-1]$​，
  $$f(i,j)=max(f(i-1,j-1)+1,f(i-1,j),f(i,j-1))$$
  反之，
  $$f(i,j)=max(f(i-1,j-1),f(i-1,j),f(i,j-1))$$

• 结果：$f(m,n)$

代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
	string s1, s2;
	while (cin >> s1 >> s2)
	{
		vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
		for (int i = 1; i <= s1.size(); ++i)
		{
			for (int j = 1; j <= s2.size(); ++j)
			{
				int sameMax = max(dp[i - 1][j], dp[i][j - 1]);
				if (s1[i - 1] == s2[j - 1])
					dp[i][j] = max(sameMax, dp[i - 1][j - 1] + 1);
				else
					dp[i][j] = max(sameMax, dp[i - 1][j - 1]);
			}
		}
		cout << dp[s1.size()][s2.size()] << endl;
	}
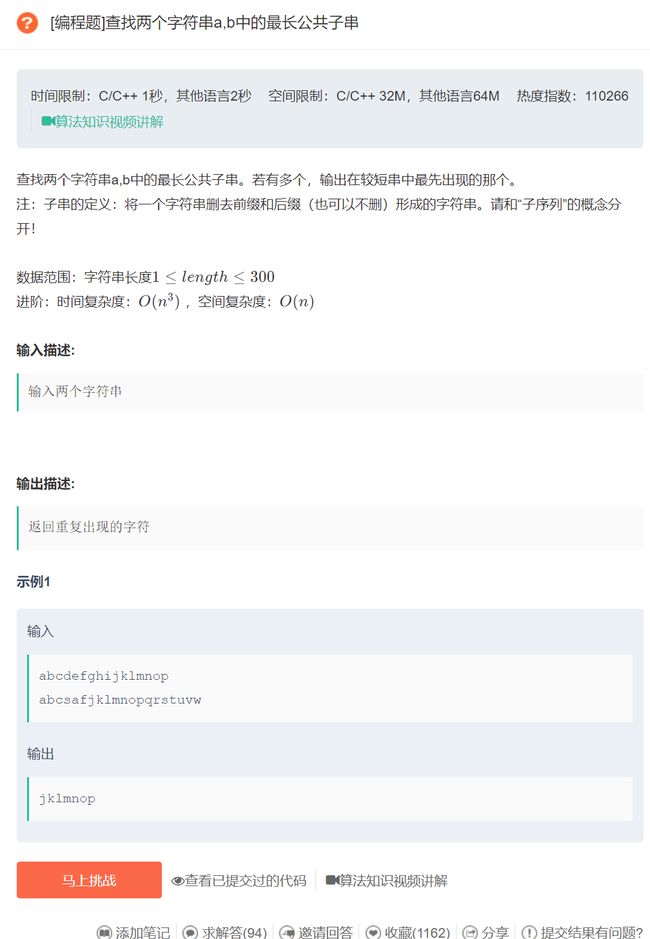
	return 0;
}

• 变式题目：

原题链接：查找两个字符串a,b中的最长公共子串

• 法一：暴力求解

算法思想：

• 直接暴力实现，将较短的串依次拆解成若干个子串substr，一一在较长串中匹配。
• 如果匹配成功，并且此时substr的长度大于目前最长的公共子串，记录此时的substr
• 如果匹配失败，则此substr以及较短串中substr后的字符串不可能再匹配上。
• eg. 较短串a：abcde ，较长串b：abdddd， substr ：abc ，此时abc不能匹配长串中的部分串，证明abcd以及abcde也不能匹配长串。
• 不断拆分较短串，直到把所有情况都拆分匹配完毕。
• 时间复杂度：$O(N^4)$ ，

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string a, b;
    string max_str;
    cin >> a >> b;
    if (a.size() > b.size())
        swap(a, b);
	
    // i下标为此子串的起点
    for (int i = 0; i < a.size(); ++i)
    {
        // j下标为此子串的终点
        for (int j = i; j < a.size(); ++j)
        {
            string tmp = a.substr(i, j - i + 1);
            // 如果匹配不上，说明以i为起点的子串后续再也不能匹配上，直接跳出
            if (b.find(tmp) == -1)
                break;
            else if (tmp.size() > max_str.size())
                max_str = tmp;
        }
    }
    cout << max_str << endl;
    return 0;
}

• 法二：递动态规划

算法思想：

• 状态：dp[i][j] —— a[0 ~ i-1] 与 b[0 ~ j-1] 的最长公共子串。
• 初始化：$dp[0][i]=dp[0][j]=0$ ，下标为0代表空串，任何串和空串匹配最长公共字符串长度都为0。
• 状态转移方程：当a[i-1]==b[j-1]时，$dp[i][j]=dp[i-1][j-1]+1$ ，不相等时，逻辑上讲，此时最长公共串长度应该为dp[i-1][j-1]，但是为了方便处理，我们将其规定$dp[i][j]=0$。
• 返回值：用一个start变量记录最长公共串的初始位置，得到最长串的长度为len ，那么最长串就是a[start ~ start+len-1]。
• 时间复杂度：$O(N^3)$

eg.

a：cbcd ，b：abcde

	“”	a	b	c	d	e
“”	0	0	0	0	0	0
c	0	0	0	1	0	0
b	0	0	1	0	0	0
c	0	0	0	2	0	0
d	0	0	0	0	3	0

⚔ 代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string a, b;
    cin >> a >> b;
    // 将a设为较短串
    if (a.size() > b.size())
        swap(a, b);
    int m = a.size();
    int n = b.size();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    int start = 0;
    int len = 0;

    for (int i = 1; i <= m; ++i)
    {
        for (int j = 1; j <= n; ++j)
        {
            if (a[i - 1] == b[j - 1])
            {
                dp[i][j] = dp[i - 1][j - 1] + 1;
                if (dp[i][j] > len)
                {
                    len = dp[i][j];
                    start = i - len;
                }
            }
        }
    }

    cout << a.substr(start, len) << endl;
    return 0;
}

优化意见：

题目中的最优空间复杂度是$O(N)$，说明我们空间上还没有做到最优。我们观察到，动态规划dp[i][j]只与dp[i-1][j-1]有关，所以我们只需要前一行的前一个数据即可，我们可以用一维数组实现，具体实现可以自行尝试。

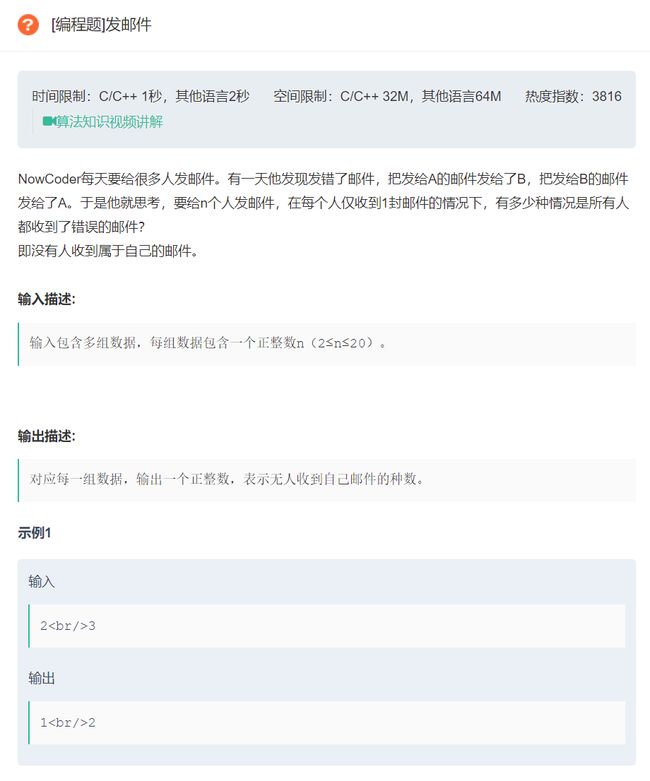
7.发邮件

---

原题链接：发邮件

算法思想：

• 一道经典的错拿问题：
• n个人都收到错误邮件的情况数我们设为f(n)，可以分为以下情况讨论：
  • 前提条件：m的邮件没有被m拿到，其他n - 1个人都有可能拿到，即有n - 1种情况。
  • 假设k拿到了m的邮件，那么对于k的邮件有两种情况：
• case1 ：是k的邮件被m拿到了，也就是m、k互相拿到了对方的邮件，那么对于其他n - 2个人互相拿错又是一个子问题f(n - 2)。
• case2 ：是k的邮件没有被m拿到，这时要保证在除了k的n - 1个人中m不能拿到k的邮件，其他人也不能拿到自己的名字，则剩下的问题是子问题f(n - 1)。（此时，在n - 1个人中，相当于m的名字变成了k，而规定自己不能拿自己的名字，所以问题又变成了f(n - 1)。）
• 因此可得递推公式$f(n)=(n-1)\ast (f(n-1)+f(n-2))$。
• 易得，f(1) = 0， f(2) = 1。

代码实现：

• 递归实现：

#include 
#include 
using namespace std;

long long misCatch(long long n)
{
    if (n == 1)
        return 0;
    if (n == 2)
        return 1;

    return (n - 1) * (misCatch(n - 1) + misCatch(n - 2));
}

int main()
{
    long long n;
    while (cin >> n)
    {
        cout << misCatch(n) << endl;
    }
    return 0;
}

• 动态规划实现：

#include 
#include 
using namespace std;

int main()
{
    int n;
    while (cin >> n)
    {
        vector<long long> v(n + 1, 0);
        v[2] = 1;
        for (int i = 3; i <= n; ++i)
        {
            v[i] = (i - 1) * (v[i - 1] + v[i - 2]);
        }

        cout << v.back() << endl;
    }
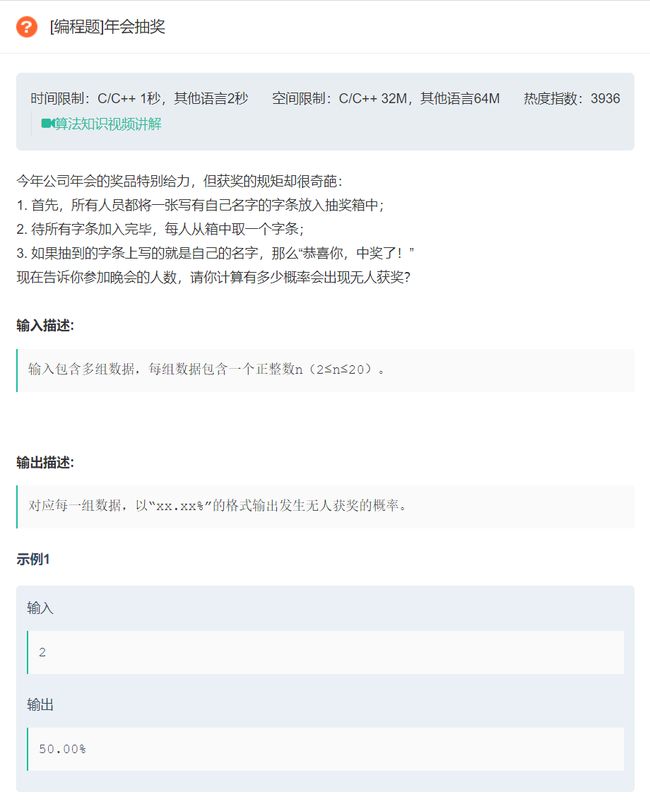
    return 0;
}

• 同类题目：

原题链接：年会抽奖

算法思想：

• 这是一道考验排列组合的题目，这里我们可以使用元素法：无人获奖的概率 = 无人获奖的全部情况数 / 抽奖的所有情况数。

• 设一共有n个人参与抽奖。

• $抽奖的所有情况数=A_n^n$ ，也就是排列数。

• n个人中无人获奖的情况数我们设为f(n)，可以分为以下情况讨论：

  • 前提条件：m的名字没有被m拿到，其他n - 1个人都有可能拿到，即有n - 1种情况。
  • 假设k拿到了m的名字，那么对于k的名字有两种情况：

• case1 ：是k的名字被m拿到了，也就是m、k互相拿到了对方的名字，那么对于其他n - 2个人互相拿错又是一个子问题f(n - 2)。

• case2 ：是k的名字没有被m拿到，这时要保证在除了k的n - 1个人中m不能拿到k的名字，其他人也不能拿到自己的名字，则剩下的问题是子问题f(n - 1)。（此时，在n - 1个人中，相当于m的名字变成了k，而规定自己不能拿自己的名字，所以问题又变成了f(n - 1)。）

• 因此可得递推公式$f(n)=(n-1)\ast (f(n-1)+f(n-2))$。

• 易得，f(1) = 0， f(2) = 1。

• 所以 $P=f(n)/A_n^n$ 。

代码实现：

• 递归：

#include 
using namespace std;
// 求无人获奖的情况数
long long getFunc(int n)
{
    if (n == 2)
        return 1;
    if (n == 1)
        return 0;
    return (n - 1) * (getFunc(n - 1) + getFunc(n - 2));
}
// 求排列数
long long getSum(int n)
{
    if (n == 1)
        return 1;
    return n * getSum(n - 1);
}

int main()
{
    int n;
    while (cin >> n)
    {
        printf("%.2f%%\n", 1.0 * getFunc(n) / getSum(n) * 100);
    }
    return 0;
}

• 迭代：

#include 
#include 
using namespace std;

int main()
{
    int n;
    vector<long long> sum(21), v(21);
    sum[1] = 1;
    sum[2] = 2;
    v[1] = 0;
    v[2] = 1;
    for (int i = 3; i <= 20; ++i)
    {
        sum[i] = i * sum[i - 1];
        v[i] = (i - 1) * (v[i - 1] + v[i - 2]);
    }
    while (cin >> n)
    {
        printf("%2.2f%%", 1.0 * v[n] / sum[n] * 100);
    }
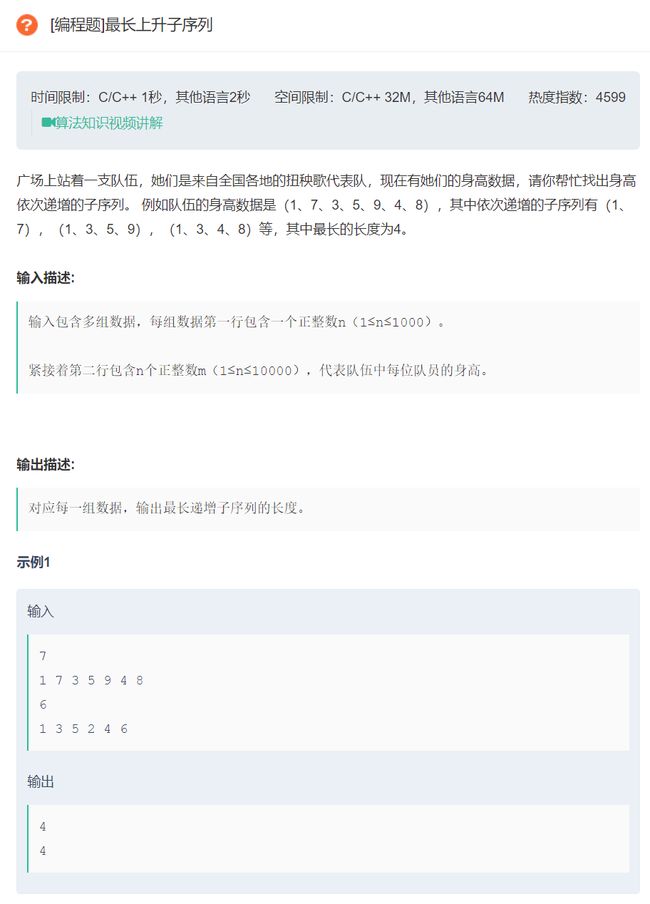
    return 0;
}

---

8.最长上升子序列

---

原题链接：最长上升子序列

算法思想：

• 动态规划经典题目，设v为存放输入序列的数组，dp为动态规划数组。

• 状态：$dp[i]$ —— 前i个元素的最长上升子序列的长度。

• 初始值：$dp[i]=1$ ，每一个值都可以自己构成只有一个元素的最长上升子序列。

• 状态转移方程：如果$v[i]>v[j](i>j)$ ，
  $$dp[i]=max(dp[i],dp[j]+1)$$

• 返回值：$max(dp[i])$

代码实现：

#include 
#include 
using namespace std;

int main()
{
    int n;
    while (cin >> n)
    {
        vector<int> v(n);
        for (int i = 0; i < n; ++i)
            cin >> v[i];

        vector<int> dp(n, 1);// 初始化值都为1
        int ans = dp[0];// 记录最大上升序列
        for (int i = 1; i < n; ++i)
        {
            for (int j = 0; j < i; ++j)
            {
                if (v[j] < v[i])
                    dp[i] = max(dp[i], dp[j] + 1);
            }
            ans = max(ans, dp[i]);
        }
        cout << ans << endl;
    }
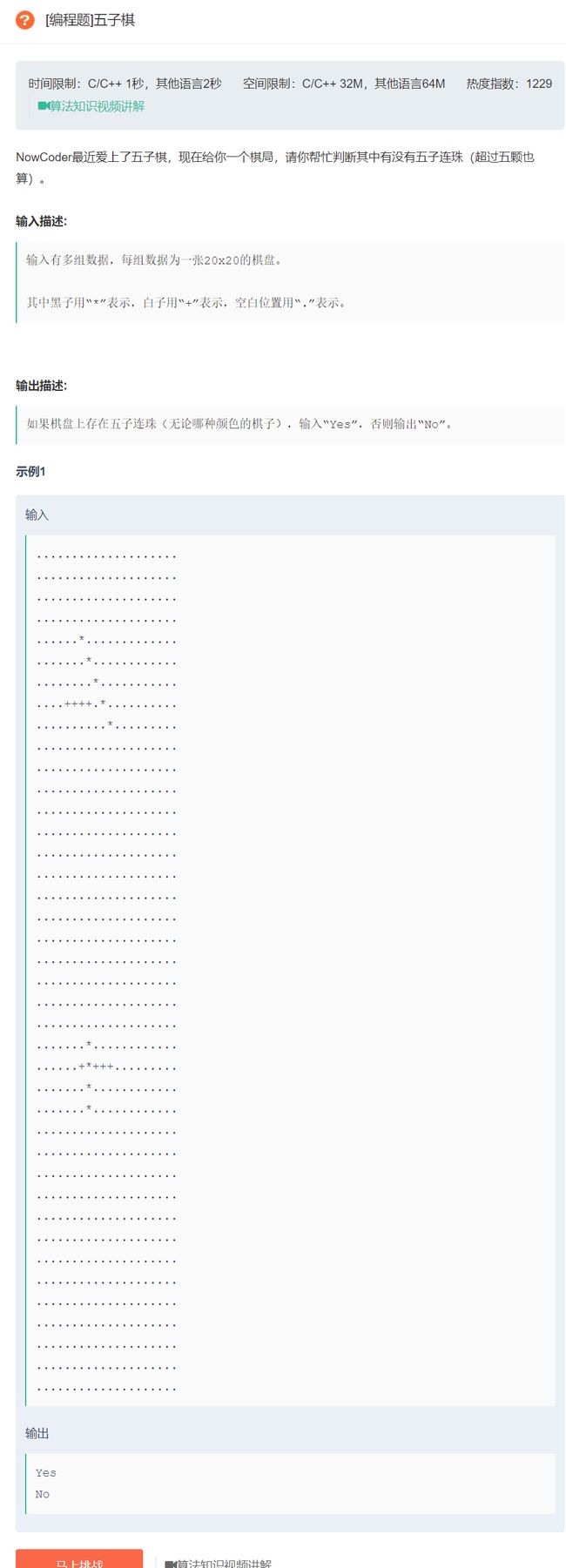
    return 0;
}

---

9.五子棋

---

原题链接：五子棋

算法思想：

• 思路比较简单，从上到下，从左到右遍历整个棋盘，发现有黑子或者白子就进行判断。
• 判断思路：
  • 首先，从这个位置开始，向右找相同的棋子，不断向右直到棋子不同，记录相同棋子的个数，如果大于等于5个就获胜，反之，走下面的逻辑。
  • 其次，从这个位置开始向下找，同上，如果大于等于5个就获胜，反之，走下面的逻辑。
  • 最后，从这个位置开始向右下找，同上，如果大于等于5个就获胜。
  • 如果以上都不满足，那么未获胜，继续遍历棋盘。
• 这里不用向上，左，左上找的原因是：我们是从左上遍历到右下，如果上，左，左上有胜利的条件，在前面就会被找到。

代码实现：

#include 
#include 
#include 
using namespace std;
// 棋盘大小
#define BOARDSIZE 20

// 判断是否胜利
bool isWin(vector<vector<char>>& vv, char ch, int x, int y)
{
	int num = 0;// 记录相同子的数量
	int tmpx = x, tmpy = y;// 记录循环中的临时位置

	// 向右找
	while (tmpx < vv.size() && tmpy < vv[0].size())
	{
		if (vv[tmpx][tmpy] == ch)
			num++;
		else
			break;
		tmpy++;
	}
	if (num >= 5)
		return true;
	// 向下找
	num = 0;
	tmpx = x, tmpy = y;
	while (tmpx < vv.size() && tmpy < vv[0].size())
	{
		if (vv[tmpx][tmpy] == ch)
			num++;
		else
			break;
		tmpx++;
	}
	if (num >= 5)
		return true;
	// 向右下找
	num = 0;
	tmpx = x, tmpy = y;
	while (tmpx < vv.size() && tmpy < vv[0].size())
	{
		if (vv[tmpx][tmpy] == ch)
			num++;
		else
			break;
		tmpx++;
		tmpy++;
	}
	if (num >= 5)
		return true;
	return false;
}

int main()
{
	vector<vector<char>> vv(BOARDSIZE, vector<char>(BOARDSIZE));
	
	begin:
	while (cin >> vv[0][0])
	{
		for (int i = 0; i < BOARDSIZE; ++i)
		{
			for (int j = 0; j < BOARDSIZE; ++j)
			{
				if (i == 0 && j == 0)
					continue;
				cin >> vv[i][j];
			}
		}

		for (int i = 0; i < BOARDSIZE; ++i)
		{
			for (int j = 0; j < BOARDSIZE; ++j)
			{
				if (vv[i][j] == '*' || vv[i][j] == '+')
				{
                    // 判断胜利
					if (isWin(vv, vv[i][j], i, j))
					{
                        // 胜利直接回到输入数据的位置
						cout << "Yes" << endl;
						goto begin;
					}
				}
			}
		}
        // 没有胜利的一方
		cout << "No" << endl;
	}
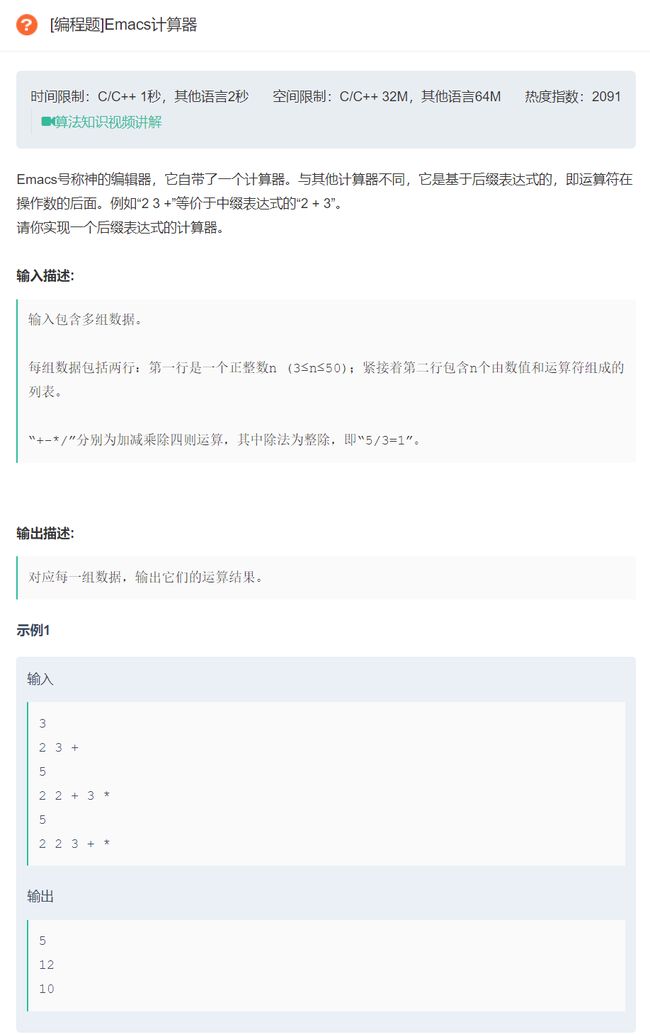
	return 0;
}

---

10.Emacs计算器

---

原题链接：Emacs计算器

先说一下这道题的意思，给一组后序的算式，要求计算结果。后序表达式是计算机经常使用的表达式，因为后序比中序更优的点是：不用加括号判断符号的优先级，遇到符号直接进行拿这个符号前面的两个数计算即可，计算后的结果作为结果继续加入后续运算。并且，将中序表达式转换为后序表达式也是一个比较经典的编程题目。

补充一下：所谓中序表达式和后序表达式就是将算式转化成一棵二叉树，然后对其进行中序遍历和后序遍历所得到的结果。

算法思想：

• 直接使用栈结构存储输入的数，遇到符号，直接出栈两个数进行运算，再将结果入栈，继续进行运算，直到算式输入完毕。
• 如果不理解中序表达式和后序表达式的概念，可以去了解一下，这对于这道题能否被做出来有决定作用。

代码实现：

#include 
#include 
#include 
#include 
using namespace std;

int main()
{
	int n;
	while (cin >> n)
	{
		stack<int> st;
		string tmp;
		for (int i = 0; i < n; ++i)
		{
			cin >> tmp;
            // 如果这个字符串是数字，直接入栈
			if (isdigit(tmp[0]))
				st.push(stoi(tmp));
            // 如果是符号，进行运算
			else
			{
                // 注意，取数时，栈顶的数是第二个运算数，栈顶的下一个数是第一个运算数
				int num2 = st.top();
				st.pop();
				int num1 = st.top();
				st.pop();
				int result = 0;
				// 根据符号进行运算
				if (tmp == "+")
					result = num1 + num2;
				else if (tmp == "-")
					result = num1 - num2;
				else if (tmp == "*")
					result = num1 * num2;
				else if (tmp == "/")
					result = num1 / num2;
                // 结果入栈继续参与后续运算
				st.push(result);
			}
		}
		cout << st.top() << endl;
	}
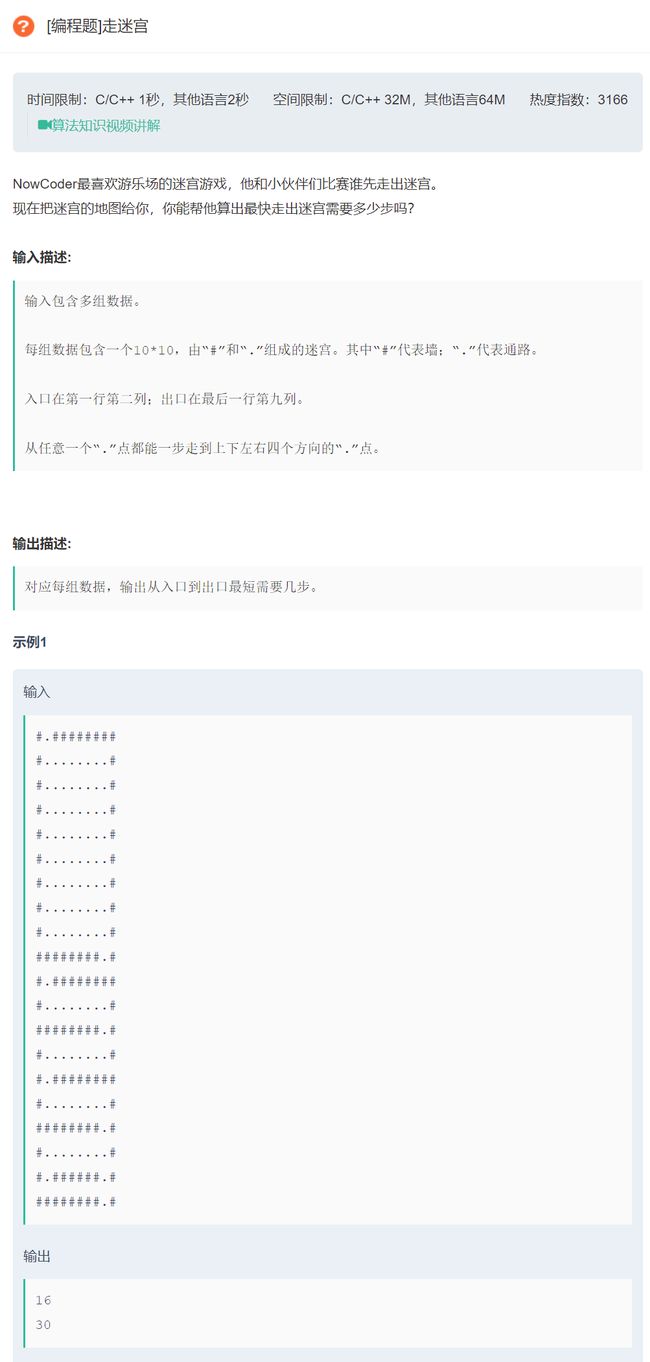
	return 0;
}

---

11.走迷宫

---

原题链接：走迷宫

算法思想：

• 一眼深度优先搜索（如果不了解深度优先搜索算法的，可以先看【刷题日记】回溯算法(深度优先搜索)经典题目），但是与普通深度优先搜索不同的是这道题目需要求出最短的步数，所以我们要在原来深度优先搜索的基础上加一些改造。

  1. 用一个引用整形stplen记录最短步数，每换一个路径到终点后，比较stplen与当前步数curlen的大小，如果curlen小于stplen，那么将curlen赋值给stplen。

  2. 剪枝条件：当curlen大于等于stplen时，Dfs直接返回。因为此时的步长已经与最短步数相同了，到达终点的步数大于等于最短步数，没必要再走了。

  3. 如何防止走回头路？

     如果我们像平常一样直接设置一个bool数组来判断遍历情况，是可以有效防止走回头路，但是本题目是要求出路径中最小的，当回溯回去再次出发时，可能要走上一个路径走过的路，bool数组会出问题。

     这里，我选择在下一次Dfs开始之前将现在位置设置成#，这样可以防止走回头路。在本次Dfs结束的时候将现在位置恢复成.，这样不会影响回溯点再出发。

     当然，也可以按照上面的思路设置一个bool数组，下一次Dfs开始之前将现在位置对应的bool值设置成true，在本次Dfs结束的时候将现在位置对应的bool值恢复成false。

代码实现：

#include 
#include 
#include 
using namespace std;

// 迷宫尺寸
#define MAZESIZE 10
// 遍历方向
static int des[4][2] = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };

void Dfs(vector<vector<char>>& vv, int x, int y, int& stplen, int curlen)
{
    // 到达终点判断
	if (x == 9 && y == 8)
	{
		stplen = min(stplen, curlen);
		return;
	}

	// 剪枝，减少计算
	if (curlen >= stplen)
		return;
    // 下一次Dfs开始之前将现在位置设置成#
	vv[x][y] = '#';


	for (int i = 0; i < 4; ++i)
	{
		int newX = x + des[i][0];
		int newY = y + des[i][1];
		// 防止越界
		if (newX > 9 || newX < 0 || newY > 9 || newY < 0)
			continue;
        
		if (vv[newX][newY] == '.')
			Dfs(vv, newX, newY, stplen, curlen + 1);
	}
    // 本次Dfs结束的时候将现在位置恢复成 .
	vv[x][y] = '.';
}

int main()
{
	vector<vector<char>> vv(MAZESIZE, vector<char>(MAZESIZE));
	while (cin >> vv[0][0])
	{
		for (int i = 0; i < MAZESIZE; ++i)
		{
			for (int j = 0; j < MAZESIZE; ++j)
			{
				if (i == 0 && j == 0)
					continue;
				cin >> vv[i][j];
			}
		}
		
		int stplen = INT_MAX;
		Dfs(vv, 0, 1, stplen, 0);
		cout << stplen << endl;
	}
	return 0;
}

---

12.解读密码

---

原题链接：解读密码

算法思想：

• 直接遍历字符串选出数字字符即可。

代码实现：

#include 
#include 
#include 
using namespace std;

int main()
{
    string s;
    while(getline(cin, s))
    {
        string ans;
        for(auto& ch : s)
        {
            if(isdigit(ch))
                ans.push_back(ch);
        }
        cout << ans << endl;
    }
    return 0;
}

---

后记

---

这次题目主要集中在动态规划这个面试最爱考的题目，比较考验大家的逻辑思维以及代码实现能力，相信大家做完会有所收获。

这个是一个新的系列——《笔试经典编程题目》，隶属于【刷题日记】系列，白晨开这个系列的目的是向大家分享经典的笔试编程题，以便于大家参考，查漏补缺以及提高代码能力。如果你喜欢这个系列的话，不如关注白晨，更快看到更新呀。

本文是笔试经典编程题目的第七篇，如果喜欢这个系列的话，不如订阅【刷题日记】系列专栏，更快看到更新哟

---

如果解析有不对之处还请指正，我会尽快修改，多谢大家的包容。

如果大家喜欢这个系列，还请大家多多支持啦！

如果这篇文章有帮到你，还请给我一个大拇指 和小星星 ⭐️支持一下白晨吧！喜欢白晨【刷题日记】系列的话，不如关注白晨，以便看到最新更新哟！！！

我是不太能熬夜的白晨，我们下篇文章见。