【机器学习】李宏毅——Anomaly Detection(异常检测)
异常检测概述
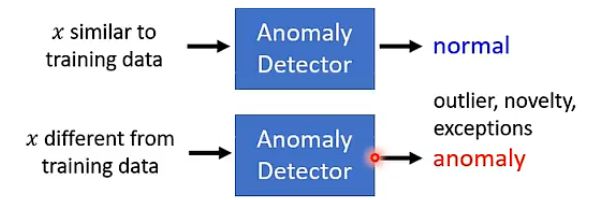
首先要明确一下什么是异常检测任务。对于异常检测任务来说,我们希望能够通过现有的样本来训练一个架构,它能够根据输入与现有样本之间是否足够相似,来告诉我们这个输入是否是异常的,例如下图:
那么这里“异常”具体的含义要根据我们训练集而定,不是说异常就一定是不好的东西,例如下面几个例子就可以更好的理解:
那么异常检测的应用场景非常地多样,例如检测消费记录是否异常、检测网络连接是否异常、检测是否异常等等。
那么这个异常检测的任务是否感觉很像二分类问题呢?即我们有正类(正常)和负类(异常)的样本,然后将其放入训练器中不断地训练最后得到想要的模型。
但实际上是很难按照这样的做法来实现的!因为正类的样本实际上我们很容易收集到,但是负类的样本可以说很难收集,或者说负类样本是无穷无尽的,没有办法让机器学习到每一种负类样本的特征,例如下图的非神奇宝贝的物品是无法穷举的:
另外一个问题是异常的例子通常很难被收集到,例如网络的异常访问或者异常的交易数据等等,都是在大量的正常数据中才能够找到一个异常数据,因此这也是很严重的问题。
现在我们需要理清楚我们的思路和策略,对于我们当前想要用来做异常检测所拥有的 { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN},可能会有以下几种情况:
- 这些样本是拥有label的,即 { y ^ 1 , . . . , y ^ N } \{\hat{y}^1,...,\hat{y}^N\} {y^1,...,y^N},那么我们就可以用来训练一个分类器;但是我们希望分类器在见到某种样本和当前已知的数据集中的样本不接近,可以认为是机器没有见过的样本时,它能够为该样本贴上标签为"unknown",这种称为Open-set Recognition
- 这些样本是没有label的,这种情况就需要再进行划分
- 拥有的这些样本都是正类样本,即这些样本都是“干净”的
- 拥有的这些样本之中存在部分异常样本,即这些样本是受到“污染”的
下面对各个情况进行介绍
Case 1:存在标签
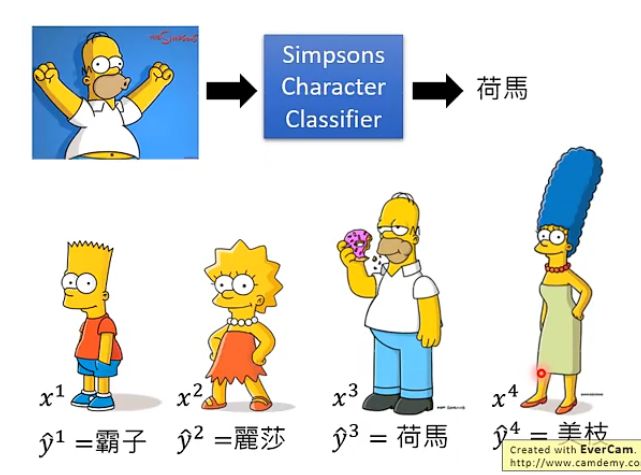
我们从辛普森家族的例子来进行讲解,假设当前收集了很多该家族的图片并加上了标签,即:
那我们希望就是训练一个分类器,它能够读取一张图片并作出预测,预测它是这个家族中的谁。
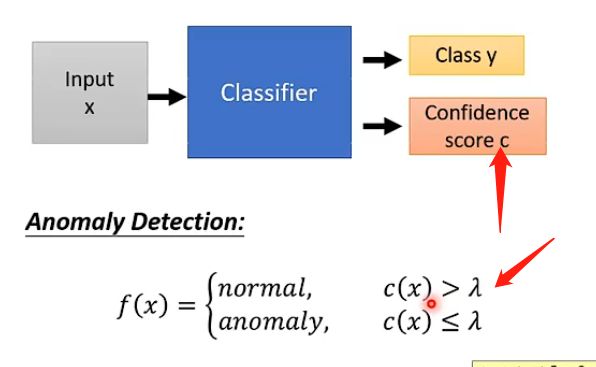
那么如何将这个任务和异常检测挂钩呢,或者说我们如何检测不是这个家族的人的图像呢?具体的做法是:我们可以让分类器在输出类别的时候同时也输出一个数值,该数值表示它认为这张图片是这个类别的信心有多大,那么我们事先也设定一个阈值 λ \lambda λ,如果信心大于阈值则说明机器认为是这个家族中的人,则可以认为是正常的;否则说明机器很没有信心,那么就很有可能不是该家族中的人,如下图:
那么如何来计算这个Confidence score呢?常见的方法就是如果机器的输出是一个向量,记录了它认为分类是哪一个类别的各个概率/信息,那我们可以取该向量中的最大值来作为信心分数,因为如果机器很肯定那么其最大值肯定很大,否则就会很平均,最大值也会比较小,如下图;
或者我们也可以将这个向量看成一个概率分布,然后计算该概率分布的信息熵,因为对于概率分布来说如果它的各个取值的概率越平均则信息熵越大,否则信息熵越小,那么上面的例子中就是第一个的信息熵很小,第二个的信息熵很大,那么我们就要设定小于阈值才是正常的,大于才是不正常的。
但是这样的方法可能存在一定的问题,就是它可能只学习到正常样本的某种特别明显的标签而已,例如这样就很可能只学习到辛普森家族的人物的脸都是黄色的,那么如果将其他异常样本也涂成黄色的,那么就很可能可以得到很高的信心分数:
那么这个问题的根本原因可能是异常样本实在是太少了,那么解决的办法也有,类似于可以用GAN来生成异常样本,然后需要教机器如果看到异常的样本就需要给它较低的信心分数,说到底还是通过增加异常样本来缓解该问题。
Example Framework
我们现在来将系统的流程进行梳理:
- 训练的时候我们很多辛普森家族任务的照片和对应的标签,并训练一个分类器,它能够告诉我们训练集中的图片是哪一个辛普森家族的人物并给予一个信心分数
- 而我们另外训练一个 Development Set,这个集里面有很多图片,包含着是辛普森家族的图片和不是辛普森家族的图片,且带有对应的标签,这个集合的作用就是用来检测分类器的好坏,同时将阈值调整到能够在该集合上表现最好
- 用测试集来进行检测和计算泛化性能
而如何衡量分类器的好坏通常不是用正确率这个指标的,因为在异常检测的大部分场景之中正常样本和异常样本的分布过于悬殊,很可能是好几百比一的比例,那这样的话如果机器不管看到什么样本都直接说是正常的,也能够得到很高的正确率。这并不是我们想要的机器!
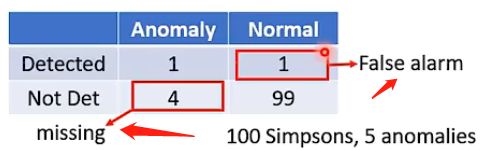
一般来说异常检测系统的分类结果可能会有以下几个可能:
那么错误的情况就是两种:将正常的检测为异常的和将异常的检测为正常的。
那么如何评价这种分类结果的好坏其实就取决你觉得哪一个分类错误更加严重,哪一种更严重就设置更高的惩罚。
Case 2:不存在标签
对于不存在标签的情况,也就是我们只有 { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN},而没有 { y ^ 1 , . . . , y ^ N } \{\hat{y}^1,...,\hat{y}^N\} {y^1,...,y^N},也就是说我们无法训练一个分类器来帮助我们进行异常检测。
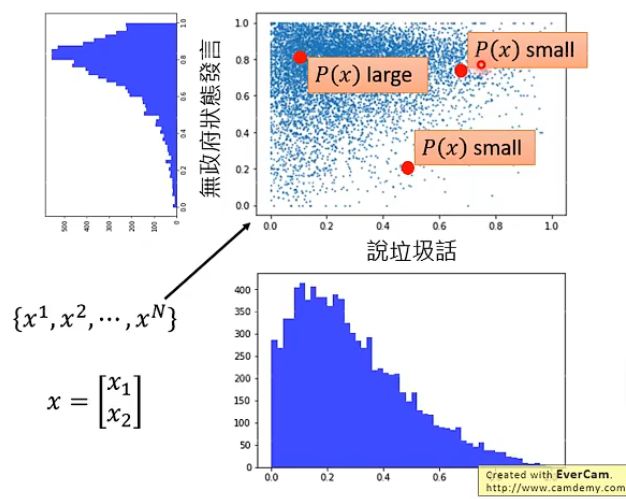
那我们的具体想法就是根据样本数据产生一个分布 P ( x ) P(x) P(x),正常的样本在该分布中得到的概率就高,异常的样本概率就低,那就可以类似地设置一个阈值将正常和异常的样本区分开。例如下图:
那么接下来的问题就是如何寻找这个分布呢?我们可以假设存在一个概率密度函数 f θ ( x ) f_{\theta}(x) fθ(x),那么代入某一个样本后得到的值就是该样本被取样得到的概率。那么根据极大似然的思想,可以知道应该要找到对应的 f θ ( x ) f_{\theta}(x) fθ(x)可以使得 { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN}这些样本一起出现的概率最大,即
L ( θ ) = f θ ( x 1 ) f θ ( x 2 ) . . . f θ ( x N ) θ ∗ = a r g m a x θ L ( θ ) L(\theta)=f_{\theta}(x^1)f_{\theta}(x^2)...f_{\theta}(x^N)\\\theta^*=argmax_{\theta}L(\theta) L(θ)=fθ(x1)fθ(x2)...fθ(xN)θ∗=argmaxθL(θ)
如果不明确极大似然估计的思想,那么可以这样简单理解:我们拥有的这些样本可以认为是从某个分布之中不断采样得到的,那么拥有 { x 1 , x 2 , . . . , x N } \{x^1,x^2,...,x^N\} {x1,x2,...,xN}可以认为是一个事件,既然这个事件已经发生了,那么我们应该觉得这个事件在所有事件中的发生概率应该是最大的,那么它才会发生,而这个“所有事件”实际上就是由 θ \theta θ不同才引起的 f θ ( x ) f_{\theta}(x) fθ(x)不同,而产生的不同事件。
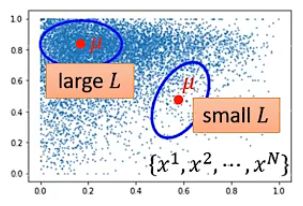
而常见的,是将该概率分布设为高斯分布:
f μ , Σ ( x ) = 1 ( 2 π ) D 2 1 ∣ Σ ∣ 1 2 e x p { − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) } μ ∗ , Σ ∗ = a r g m a x μ , Σ L ( μ , Σ ) f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{\vert \Sigma \vert ^{\frac{1}{2}}}exp\{-\frac{1}{2} (x-\mu)^T\Sigma^{-1} (x-\mu) \}\\\mu^*,\Sigma^*=argmax_{\mu,\Sigma}L(\mu,\Sigma) fμ,Σ(x)=(2π)2D1∣Σ∣211exp{−21(x−μ)TΣ−1(x−μ)}μ∗,Σ∗=argmaxμ,ΣL(μ,Σ)
直观上看不同的参数所带来的影响:
上述式子可以解出来:
μ ∗ = 1 N ∑ n = 1 N x n Σ ∗ = 1 N ∑ n = 1 N ( x − μ ∗ ) ( x − μ ∗ ) T \mu^*=\frac{1}{N}\sum_{n=1}^Nx^n\\\Sigma^*=\frac{1}{N}\sum_{n=1}^N(x-\mu^*)(x-\mu^*)^T μ∗=N1n=1∑NxnΣ∗=N1n=1∑N(x−μ∗)(x−μ∗)T
因此我们的异常检测系统也就明确的,即:
而由于高斯分布可以有很多维度,因此可以选取很多的特征来加入这个模型,可能可以使得结果更为精确。并且在实际场景中可以将f(x)加上一个log,因为概率的限制,加上log之后的取值范围会更大,我们可以找到更好的区分点。