论文记录：Topology-aware Convolutional Neural Network for Efficient Skeleton-based Action Recognition

论文记录：Topology-aware Convolutional Neural Network for Efficient Skeleton-based Action Recognition(AAAI 2022)

---

论文地址:https://arxiv.org/abs/2112.04178
代码地址:https://github.com/hikvision-research/skelact

Abstract

• 本文提出了一种纯CNN结构，名为拓扑感知CNN（Ta-CNN）,包括CAG和VAG模块，缓解了CNN在不规则骨架拓扑建模差的问题。
• 理论上分析了图卷积和普通卷积的关系，证实GCN的建模能力，使用CNN也能实现。
• 提出SkeletonMix策略，进行数据增强。

---

Method

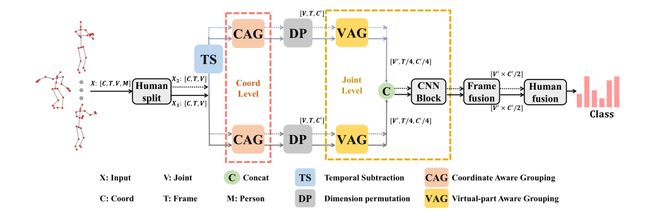
骨骼行为识别任务的输入是一系列骨架数据 $X\in R^{C\times T\times V}$,$C$、$T$和$V$分别代表坐标维度、时间序列长度和关节数。将C作为图像数据的通道，T、V作为图像的宽、高来进行卷积(和HCN一样)。

CAG模块

作者为了验证不同坐标重要性的假设做了一个小实验，最后得到的结论是坐标的特征更加重要。
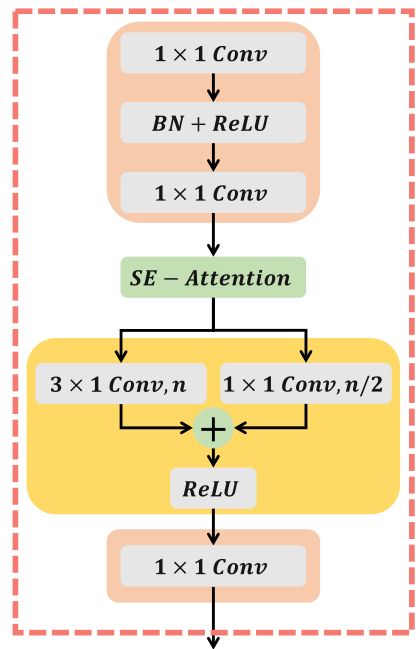
坐标感知分组(CAG)模块分为三个步骤，分别为Feature Mapping,Channel attention,Dual Coordinate-wise Convolution.\

• Feature Mapping： 几个逐点卷积+BN层
• Channel attention： 一个通道注意力模块
• Dual Coordinate-wise Convolution： 分为了两个branch，其实就是分组的Channel-wise卷积，两个分支分别分为n组和n/2组，分别提取不同粒度特征。
  CAG模块的结构图：
  

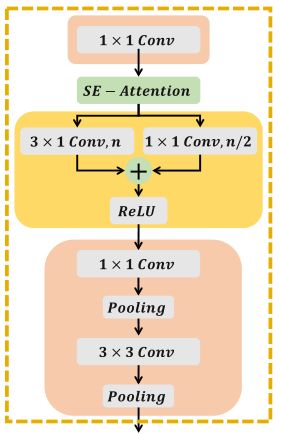
VAG模块

VAG模块结构和CAG相比稍作调整，但是VAG模块是在关节维度而非坐标维度上做的。作者在文中说，通过两个分组卷积分支，可以将虚拟关节划分为多个虚拟部分。该模块结构如下：

图卷积可看作为一种特殊的普通卷积

对于输入的骨架序列 $X\in R^{C\times T\times V}$，图卷积的过程可看作：
$Y=WXA$
其中$A\in R^{V\times V}$为邻接矩阵，表示骨架拓扑信息，$W\in R^{C^{\prime }\times C}$为权重矩阵。如果忽视特征变换，其核心计算为
$Y_{c,t,v}={\sum }_{u=0}^{V-1}{X}_{c,t,u}{A}_{u,v}$
可以看出GCN的本质是在邻接矩阵的指导下，通过加权平均来聚合所有关节的时空特征。
现在把关节维度看作通道，即输入$X\in R^{V\times T\times C}$，对输入做一个$P\times Q$的卷积，式子为
$Y_{v,t,c}={\sum }_{u=0}^{V-1}{\sum }_{p=0}^{P-1}{\sum }_{q=0}^{Q-1}{\omega }_{v,u,p,q}{X}_{u,t+p-P/2,c+q-Q/2}$
当卷积核大小为$1\times 1$时，则上式简化为
$Y_{v,t,c}={\sum }_{u=0}^{V-1}{\omega }_{v,u}{X}_{u,t,c}$
从这个式子看出，当输入通道和输出通道相同，邻接矩阵作为权重，卷积则等价于图卷积。作者表示如果使用更大卷积核则可以感知更多信息。并且CNN相比GCN更加灵活。

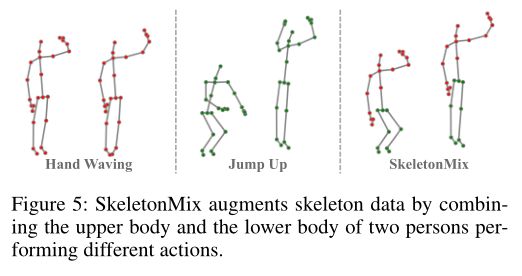
SkeletonMix

这里做了个数据增强，将两个不同动作的骨架，一个取上半身一个取下半身拼接在一起。示意图：

Ta CNN框架

采用双流网络，一个输入skeleton信息，一个输入motion信息。