Pytorch总结四之 多层感知机原理及简洁实现
Pytorch总结四之 多层感知机
前边已经介绍了包括线性回归☞666和softmax回归☞666在内的单层神经⽹络。然⽽深度学习主要关注多层模型。
在本节中,我们将以多层感知机(multilayer perceptron,MLP)为例,介绍多层神经⽹络的概念。
1.隐藏层
- 多层感知机在单层神经⽹络的基础上引⼊了⼀到多个隐藏层(hidden layer)。隐藏层位于输⼊层和输出层之间。图3.3展示了⼀个多层感知机的神经⽹络图,它含有⼀个隐藏层,该层中有5个隐藏单元。
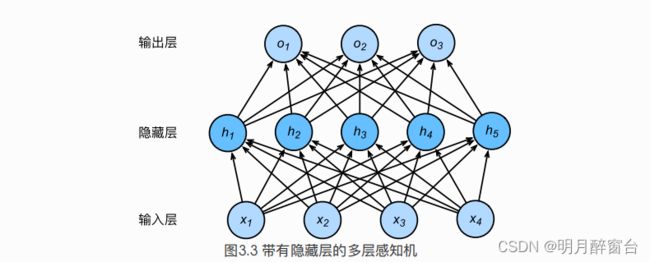
- 在图3.3所示的多层感知机中,输⼊和输出个数分别为4和3,中间的隐藏层中包含了5个隐藏单元
(hidden unit)。由于输⼊层不涉及计算,图3.3中的多层感知机的层数为2。由图3.3可⻅,隐藏层中的神经元和输⼊层中各个输⼊完全连接,输出层中的神经元和隐藏层中的各个神经元也完全连接。因此,多层感知机中的隐藏层和输出层都是全连接层。

2. 激活函数
上述问题的根源在于全连接层只是对数据做仿射变换(affine transformation),⽽多个仿射变换的叠加仍然是⼀个仿射变换。解决问题的⼀个⽅法是引⼊⾮线性变换,例如对隐藏变量使⽤按元素运算的⾮线性函数进⾏变换,然后再作为下⼀个全连接层的输⼊。这个⾮线性函数被称为激活函数(activation function)。下⾯我们介绍⼏个常⽤的激活函数。
2.1 Relu函数
ReLU(rectified linear unit)函数提供了⼀个很简单的⾮线性变换。给定元素 ,该函数定义为:

可以看出,ReLU函数只保留正数元素,并将负数元素清零。为了直观地观察这⼀⾮线性变换,我们先定义⼀个绘图函数 xyplot 。
%matplotlib inline
import torch
import numpy as np
import matplotlib.pylab as plt
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
def xyplot(x_vals, y_vals, name):
d2l.set_figsize(figsize=(5, 2.5))
d2l.plt.plot(x_vals.detach().numpy(), y_vals.detach().numpy())
d2l.plt.xlabel('x')
d2l.plt.ylabel(name + '(x)')
# 定义自变量x范围
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
接下来通过 NDArray 提供的 relu 函数来绘制ReLU函数。可以看到,该激活函数是⼀个两段线性
函数。
#1.绘制Relu激活函数
y = x.relu()
xyplot(x, y, 'relu')
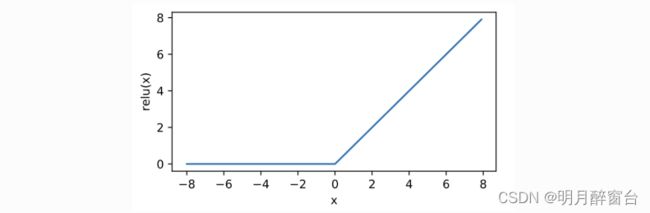
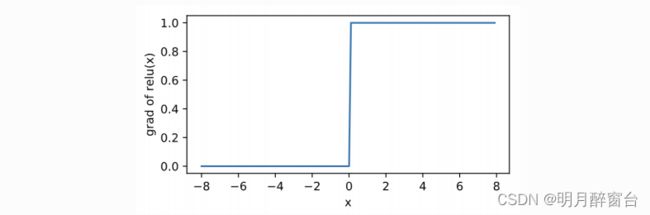
显然,当输⼊为负数时,ReLU函数的导数为0;当输⼊为正数时,ReLU函数的导数为1。尽管输⼊为0 时ReLU函数不可导,但是我们可以取此处的导数为0。下⾯绘制ReLU函数的导数。
#绘制导数
y.sum().backward()
xyplot(x, x.grad, 'grad of relu')
2.2 sigmoid函数
sigmoid函数可以将元素的值变换到0和1之间:

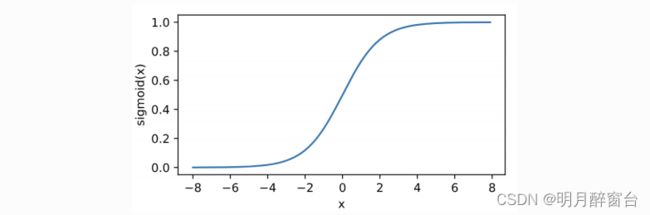
sigmoid函数在早期的神经⽹络中较为普遍,但它⽬前逐渐被更简单的ReLU函数取代。在后⾯“循环神经⽹络”⼀章中我们会介绍如何利⽤它值域在0到1之间这⼀特性来控制信息在神经⽹络中的流动。下⾯绘制了sigmoid函数。当输⼊接近0时,sigmoid函数接近线性变换。
#2.绘制sigmid函数
y = x.sigmoid()
xyplot(x, y, 'sigmoid')
#x.grad.zero_() #此句无用,加上报错,删掉也可绘制如下结果
y.sum().backward()
xyplot(x, x.grad, 'grad of sigmoid')
2.3 tanh函数

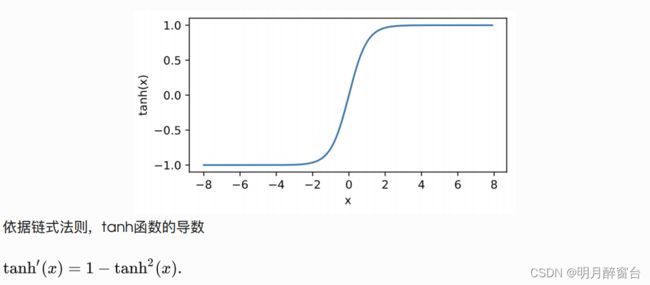
我们接着绘制tanh函数。当输⼊接近0时,tanh函数接近线性变换。虽然该函数的形状和sigmoid函数
的形状很像,但tanh函数在坐标系的原点上对称。
#3.绘制tanh函数
y = x.tanh()
xyplot(x, y, 'tanh')
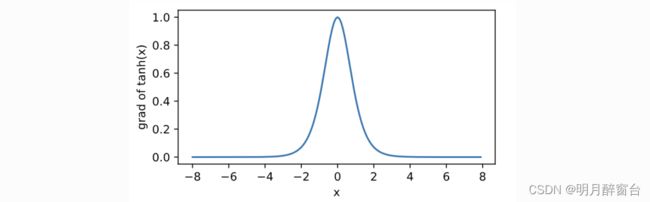
下⾯绘制了tanh函数的导数。当输⼊为0时,tanh函数的导数达到最⼤值1;当输⼊越偏离0时,tanh
函数的导数越接近0。
#x.grad.zero_()
y.sum().backward()
xyplot(x, x.grad, 'grad of tanh')
3. 多层感知机
- 多层感知机就是含有至少一个隐藏层的由全连接层组成的神经网络,且每个隐藏层的输出通过激活函数进行变换。
- 多层感知机的层数和各隐藏层中隐藏单元个数都是超参数。以单隐藏层为例,多层感知机按以下方式计算输出:

4. 多层感知机的简洁实现
#4.多层感知机的简洁实现
#4.1导入模块
import torch
from torch import nn
from torch.nn import init
import numpy as np
import sys
sys.path.append("..")
import d2lzh_pytorch as d2l
#4.2 定义模型,同soft回归不同的是,多加了一个全连接层为隐藏层,隐藏单元个数为256,
#并使用Relu函数作为激活函数
num_inputs,num_outputs,num_hiddens=784,10,256
net=nn.Sequential(d2l.FlattenLayer(),
nn.Linear(num_inputs,num_hiddens),
nn.ReLU(),
nn.Linear(num_hiddens,num_outputs))
for params in net.parameters():
init.normal_(params,mean=0,std=0.01)
#4.2 读取数据并训练模型
#由于这⾥使⽤的是PyTorch的SGD⽽不是d2lzh_pytorch⾥⾯的sgd,所以就不存在那样学习率看起来很⼤的问题了。
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
loss = torch.nn.CrossEntropyLoss() #交叉熵损失函数
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) #梯度下降大进行学习率优化
num_epochs = 6 #迭代次数
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs,
batch_size, None, None, optimizer)
为了方便理解,贴出训练和评估准确率的源码 utils.py
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
sgd(params, lr, batch_size)
else:
optimizer.step() # “softmax回归的简洁实现”一节将用到
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
# ############################ 5.5 #########################
def evaluate_accuracy(data_iter, net,
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')):
acc_sum, n = 0.0, 0
with torch.no_grad():
for X, y in data_iter:
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout
acc_sum += (net(X.to(device)).argmax(dim=1) == y.to(device)).float().sum().cpu().item()
net.train() # 改回训练模式
else: # 自定义的模型, 3.13节之后不会用到, 不考虑GPU
if('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n