并查集(Union-Find)
目录
- 前言
-
- 路径压缩
- C++代码
- 连通块中点的数量
-
- C++代码
- 食物链(带权并查集)
-
- C++代码
前言
先来看并查集一般需要解决的问题:
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
合并操作:M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
查找操作:Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
引入并查集的道理很简单,上面的两个操作如果利用暴力做法复杂度较大,需要优化,先来看暴力做法:
定义:
belong[x]来存储元素x所在的集合。如果只是查询:
if(belong[a] == belong[b]),操作的时间复杂度为 O(1),问题不大。
但是对于合并操作,要么使得满足集合为belong[a]的所有点将其belong[]值改为belong[b],要么使得满足集合为belong[b]的所有点将其belong[]值改为belong[a],无论哪种,复杂度都为 O(n),当数据量较大且频繁的进行这样操作,复杂度都会大到无法承受。
并查集的代码很短,但它的思想是非常精妙的,其关键操作里的每一行代码都值得细细考量。
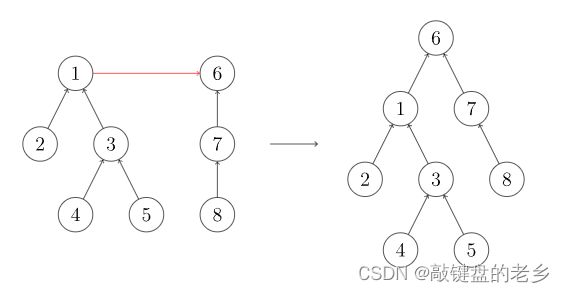
做法是将属于同一个集合的各个点放到一棵树上,每个结点x的父结点为fa[x],该树是由各个集合Union操作得来的,各结点的父结点是哪个无所谓,但这棵树的根结点一定是满足fa[x] == x,而根结点存的就是这个集合的编号,例如下图两棵树可以分别代表a与b中集合,为了方便表示,利用int。
由此,引出查找(Find)的关键操作:
int find(int x){
if(fa[x] != x) return find(fa[x]) //不是根结点就沿着父结点往上找;
else return x;
}
但是这样做的话会发现似乎复杂度并没降低得很明显,仍然像是 O(n)。
所以又引出一个新的优化操作,叫路径压缩。
路径压缩
这一操作的目的相当于是在结点找根结点过程中,发现如果x的父结点不是根结点,那么可以索性将x连接上根结点(注意这个操作不是一步到位,而是在find中递归回溯执行),这样做的好处是下次再访问或是修改x的所属集合可以一步到位了。
int find(int x){
if(fa[x] != x) fa[x] = find(fa[x]); //路径压缩
return fa[x]; //这步操作直到找到了父结点才会执行,然后回溯
}
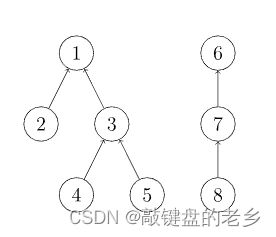
接下来就是Union操作了,合并的核心思路是既然每个集合都是树存储,那其实合并集合就是两个树连接,将其中一棵树的根结点连到另一棵树的任意结点(一般是根结点)上,这就完成了合并操作,如图所示:
fa[find(a)] = find(b);
综合起来看,两个操作的复杂度是接近 O(1) 的。
这时并查集最大优势体现出来了——存储的数据结构维护起来很方便、简洁,均是在接近 O(1) 的情况下就实现。
C++代码
#include 连通块中点的数量
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;
Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;
Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a 和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
每个连通块可以看成一个集合,集合中任意两个点间都是可达的,相较于前面,最主要的差别是要多维护一个集合中点的数量,定义size[x]来存取以x为根结点的集合中点的数量,注意size只存根结点的映射,单拎出集合中一个点来存数量不具备意义。
所以主要多了两行关键代码:
//1.初始化
size[i] = 1
//2.合并操作时更新size
size[find(b)] += size[find(a)];
C++代码
#include 食物链(带权并查集)
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A 吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1∼N 编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
当前的话与前面的某些真的话冲突,就是假话;
当前的话中 X 或 Y 比 N 大,就是假话;
当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
输入格式
第一行是两个整数 N 和 K,以一个空格分隔。
以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1,则表示 X 和 Y 是同类。
若 D=2,则表示 X 吃 Y。
输出格式
只有一个整数,表示假话的数目。
数据范围
1≤N≤50000,
0≤K≤100000
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
抽象地来讲,将某个动物的编号作为根结点(fa[x] = x),如果另一动物与该动物有关系,那么首先判断其是否在同一集合中,(这个集合就是一个语义空间),若在,则通过计算它们各自与根结点的距离进而推算出它们的关系。如果不在就需要合并它们两个集合,并且此时的说法默认为真,以此说法建立起它们的关系。
距离这一概念利用数组d[]来维护,且d[x]表示的是x到父结点的距离。
距离换算为关系的定义如下:
x 到根结点距离 (在mod 3 意义下) 为
0:x与根结点同类。
1:x可以吃根结点。
2:x被根结点吃,那么也说明可以吃“可以吃根结点”的类型动物。
具体可见代码及其注释,注意find函数在更新父结点为根结点这一操作与上面的不同之处。
C++代码
#include