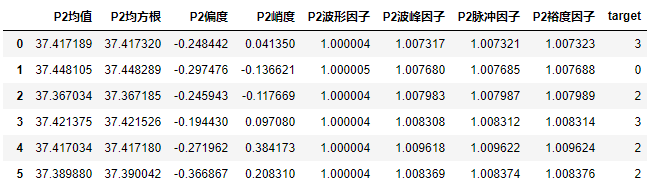
python时域波形特征分析

（一）python实现信号时域统计特征提取

https://blog.csdn.net/qq_34705900/article/details/88389319

1.实验数据需求
为了对采集的压力实验数据做特征工程，需要对信号进行时域的统计特征提取，包含了均值、均方根、偏度、峭度、波形因子、波峰因子、脉冲因子、峭度因子等，现用python对其进行实现。

2.python实现
其中的输入参数含义：

①data:实验数据的DataFrame

②p1:所截取实验信号的起始采样点位置

③p2:所截取实验信号的终止采样点位置

from pandas import Series
import math
pstf_list=[]
def  psfeatureTime(data,p1,p2):
    #均值
    df_mean=data[p1:p2].mean()
    #方差
    df_var=data[p1:p2].var()
    #标准差
    df_std=data[p1:p2].std()
    #均方根
    df_rms=math.sqrt(pow(df_mean,2) + pow(df_std,2))
    #偏度
    df_skew=data[p1:p2].skew()
    #峭度
    df_kurt=data[p1:p2].kurt()
    sum=0
    for i in range(p1,p2):
        sum+=math.sqrt(abs(data[i]))
    #波形因子
    df_boxing=df_rms / (abs(data[p1:p2]).mean())
    #峰值因子
    df_fengzhi=(max(data[p1:p2])) / df_rms
    #脉冲因子
    df_maichong=(max(data[p1:p2])) / (abs(data[p1:p2]).mean())
    #裕度因子
    df_yudu=(max(data[p1:p2])) / pow((sum/(p2-p1)),2)
    featuretime_list = [df_mean,df_rms,df_skew,df_kurt,df_boxing,df_fengzhi,df_maichong,df_yudu]
    return featuretime_list 
3.结果与说明

 

————————————————
版权声明：本文为CSDN博主「focusxy」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_34705900/article/details/88389319

（二）python时域信号特征提取

https://blog.csdn.net/weixin_43336305/article/details/103404406

def  psfeatureTime(data):
    #均值
    df_mean=data.mean()
    df_var=data.var()
    df_std=data.std()
    #均方根
    df_rms=np.sqrt(pow(df_mean,2) + pow(df_std,2))
    #峰峰值
    fengfengzhi = max(data)-min(data)
    #偏度
    df_skew=pd.Series(data).skew()
    #峰度
    df_kurt=pd.Series(data).kurt()
    sum=0
    for i in range(len(data)):
        sum+=np.sqrt(abs(data[i]))
    #波形因子
    df_boxing=df_rms / (abs(data).mean())
    #峰值因子
    df_fengzhi=(max(data)) / df_rms
    #脉冲因子
    df_maichong=(max(data)) / (abs(data).mean())
    #裕度因子
    df_yudu=max(data)/ pow(sum/(len(data)),2)
    #峭度
    df_qiaodu  =(np.sum([x**4 for x in data])/len(data)) / pow(df_rms,4)
    featuretime_list = [round(df_rms,3),round(fengfengzhi,3),round(df_fengzhi,3),round(df_boxing,3),round(df_maichong,3),round(df_yudu,3),round(df_qiaodu,3)]
    return  featuretime_list
if __name__ == '__main__':
    
    p1 = psfeatureTime(records1)
p1
def get_rms(records):
    
    """均方根值 反映的是有效值而不是平均值 """
    root_mean = math.sqrt(sum([x ** 2 for x in records]) / len(records))
    """峰峰值"""
    peak_to_peak = max(records)-min(records)
    """峰值指标"""
    crest_factor =  max(records)/root_mean
    """波形指标"""
    shape_factor = root_mean/abs(sum([x for x in records]) / len(records))
    """脉冲指标"""
    impulse_factor = max(records)/abs(sum([x for x in records]) / len(records))
    """裕度指标"""
    clarance =  max(records)/pow(abs((sum(sqrt([abs(x) for x in records]))/len(records))),2)
    """峭度指标"""
    kur =  (sum([x**4 for x in records])/len(records))/pow(root_mean,4)
    pstf = [round(root_mean,3),round(peak_to_peak,3),round(crest_factor,3),round(shape_factor,3),round(impulse_factor,3),round(clarance,3),round(kur,3)]
    return pstf
if __name__ == '__main__':
    records1 = [1, 2, 3, 4, 5, 6]
    records2 = [2, 4, 6]
       # 均方根
    rms1 = get_rms(records1)  # 4.08
    rms2 = get_rms(records2)  # 4.32
 
rms1
————————————————
版权声明：本文为CSDN博主「狂奔的 蜗牛」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/weixin_43336305/article/details/103404406

（三）信号时域分析方法的理解（峰值因子、脉冲因子、裕度因子、峭度因子、波形因子和偏度等）

https://blog.csdn.net/fengzhuqiaoqiu/article/details/101153107

最近要做关于信号处理的一些工作，涉及时域、频域分析，滤波、神经网络以及贝叶斯等内容。在此做一些整理，作为梳理思路的笔记，也希望能对读者有所帮助。

文章如要转载请私信与我联系，并注明来源知乎专栏与信号处理有关的那些东东作者Mr.括号。

时域信号可以按照有无量纲分为有量纲特征值和无量纲特征值。有量纲特征值包括：最大值、最小值、峰峰值、均值、方差、均方值、均方根值等。有量纲特征值的数值大小常因外界一些物理量的变化而变化，给工程应用带来一定困难，因而时常使用多种无量纲指标，包括峰值因子、脉冲因子、裕度因子、峭度因子、波形因子和偏度等。

这些特征量的MATLAB代码实现见：时域特征值提取的MATLAB代码实现（均方根、峰值因子、脉冲因子、裕度因子、峭度因子、波形因子和偏度等）

一、有量纲特征值

最大值、最小值、峰峰值这些就不说了。均值、方差、均方值、均方根值之间有内在的联系。

均值是信号的平均，是一阶矩，可以表示为：

均方值是信号的平方的平均（信号→平方→平均值），代表了信号的能量，是二阶矩，可以表示为：

方差是每个样本值与全体样本值的平均数之差的平方值的平均数，代表了信号能量的动态分量（均值的平方是静态分量），是二阶中心距，可以表示为：

均方根（RMS）又叫有效值。将所有值平方求和，求其均值，再开平方，就得到均方根值。

二、无量纲特征值

峰值因子是信号峰值与有效值（RMS）的比值，代表的是峰值在波形中的极端程度。

脉冲因子是信号峰值与整流平均值（绝对值的平均值）的比值。脉冲因子和峰值因子的区别在分母上，由于对于同一组数据整流平均值小于有效值，所以脉冲因子大于峰值因子。

裕度因子是信号峰值与方根幅值的比值。与峰值因子类似，方根幅值和均方根值（有效值）是对应的，均方根的公式是信号平方和的平均值的算术平方根，方根幅值是算术平方根的平均值的平方（有点绕）。

峭度因子是表示波形平缓程度的，用于描述变量的分布。正态分布的峭度等于3，峭度小于3时分布的曲线会较“平”，大于3时分布的曲线较“陡”。

综合来说：峰值因子、脉冲因子和裕度因子的物理意义是相似的，峰值因子和脉冲因子都是用来检测信号中有无冲击的指标，裕度因子常用来检测机械设备的磨损状况。峭度因子也是对振动信号冲击特性的反应，不过公式的表达形式上与前三个差异较大。

偏度：偏度也叫偏斜度、偏态。偏度和峭度是有一定的相关性的，峭度是四阶中心矩和标准差的四次方的比值；偏度是三阶中心矩和标准差的三次方的比值。偏度与峭度相同，描述的是分布。物理含义简单理解的话，对于单峰分布，负偏度代表分布图线的“头”在右侧，“尾”在左侧；正偏度反之。参看下图：

波形因子：波性因子是有效值（RMS）与整流平均值的比值。在电子领域其物理含义可以理解为直流电流相对于等功率的交流电流的比值，其值大于等于1。说到这儿也许你已经发现了，波形因子=脉冲因子/峰值因子。

欢迎关注我的公众号“括号的城堡”，微信号为“khscience”，会有更多有趣的东西分享。

参考：

Kurtosis - Wikipedia

Skewness - Wikipedia

Form factor (electronics)

高爽. 齿轮故障特征参数提取及最佳特征参数选择研究[D].沈阳航空航天大学,2017.

【图文】轴承故障诊断技术_百度文库

《故障诊断》第二章_图文_百度文库
————————————————
版权声明：本文为CSDN博主「括号先森」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/fengzhuqiaoqiu/article/details/101153107

（四）MATLAB求解峰值、均值、平均幅值、方差、均方根、方根幅值、最值、峭度、斜度、裕度指标、波形指标、脉冲指标、峰值指标、峭度指标

https://blog.csdn.net/youtaidudewamao/article/details/101981100