深度学习入门：基于Python的理论与实现

1.Python入门

python中使用class关键字来定义类：

class 类名：
	def __init__(self, 参数,...):#构造函数
		...
	def 方法1(self, 参数, ...): # 方法1
		...
	def 方法2(self, 参数, ...): # 方法2
		...

这里有一股特殊的__init__方法，这是进行初始化的方法，也叫构造函数(constructor), 只在生成类的实例时被调用一次。此外在方法的第一个参数中明确地写入表示自身（自身的实例）的self是python的一个特点

import numpy as np 
x = np.array([[1, 2], [3, 4]])
print(x)
print(x.shape)  #查看矩阵x的形状
# (2, 2)
print(x.dtype)  #查看矩阵元素的数据类型dataType
# dtype('int64')

访问元素

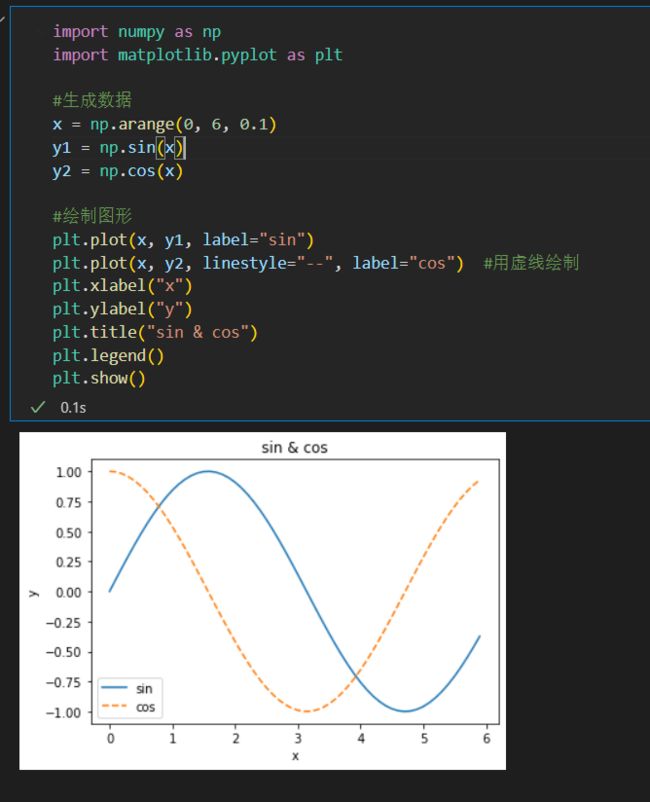
pyplot的功能

np.arange(start, end, step)
np.array([[1, 2]]) # 生成1*2维的数组

2.感知机

与门

与非门

或门

将或门的真值表可视化，可以求得w和b的值

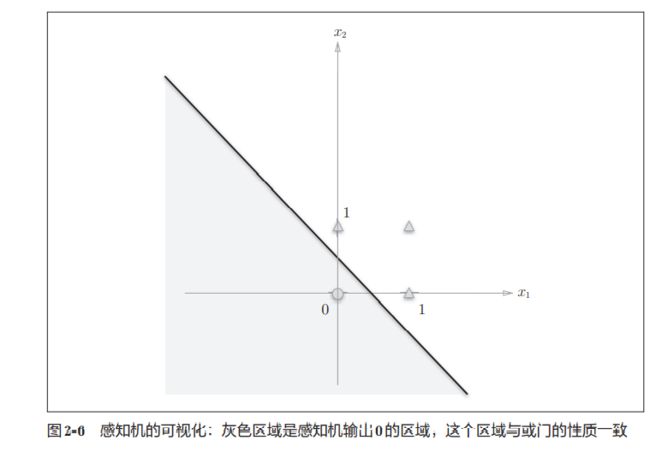
使用感知机可以实现与门，与非门，或门的逻辑电路

异或门

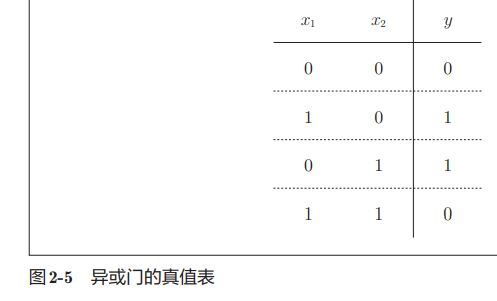
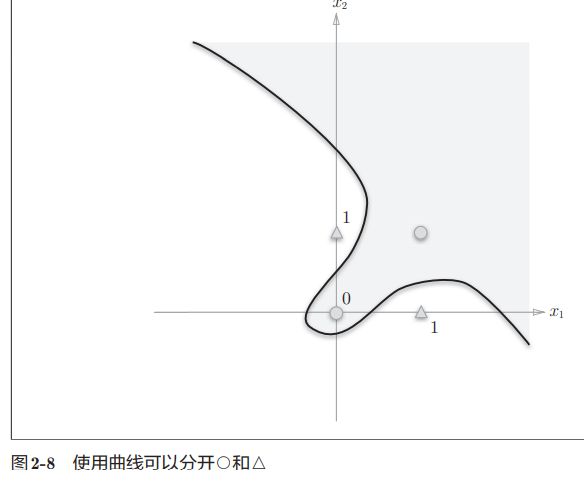
但是异或真值表不能用线性划分，只能用非线性来划分

为了表示异或门，可以用与门，与非门，或门来进行组合


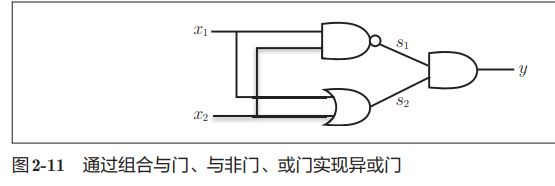
通过叠加层，感知机能进行更加灵活的表示

在用与非门等低层的元件构建计算机的情况下，分阶段地制作所需的零件（模块）会比较自然，即县实现与门和或门，然后实现半加器和全加器，接着实现算数逻辑单元ALU，然后实现CPU。

使用感知机可以表示与门和或门等逻辑电路
异或门无法通过单层感知机来表示
使用2层感知机可以表示异或门
单层感知机只能表示线性空间，而多层感知机可以表示非线性空间
多层感知机在理论上可以表示计算机

3.神经网络

阶跃函数

# 阶跃函数
def step_function(x):
    if x>0:
        return 1
    else:
        return 0
# 但是上面的参数x只能接受实数，但不允许参数为Numpy数组
# 例如step_function([1.0, 2.0])

# 下面的函数就可以接受Numpy数组
import numpy as np 
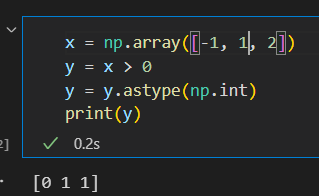
def step1_function(x):
    y = x > 0
    return y.astype(np.int)
# astype()方法通过参数指定期望的类型，这个例子中是np.int型

import numpy as np 
import matplotlib.pyplot as plt 
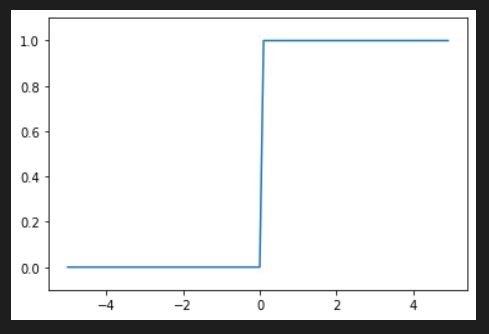
def step2_function(x):
    return np.array(x > 0, dtype=np.int)

x = np.arange(-5, 5, 0.1)
y = step2_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # 指定y轴的范围
plt.show()

sigmoid函数

import numpy as np
# 当参数x为Numpy数组时，结果也能被正确计算
def sigmoid(x):
    return 1/(1+np.exp(-x))

x = np.arange(-5, 5, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)# 指定y轴的范围
plt.show()

感知机 -->对应 阶跃函数
神经网络—> 对应 sigmoid函数
神经网络的激活函数必须使用非线性函数，即激活函数不能使用线性函数，因为如果使用线性函数，加深神经网络的层数就没有意义了，对于线性函数，不管如何加深层数，总是存在与之等效的“无隐藏层的神经网络”。为了发挥叠加层所带来的优势，激活函数必须使用非线性函数。

ReLU函数

ReLU（Rectified Linear Unit）函数，ReLU函数在输入大于0时，直接输出该值；在输入小于等于0时，输
出0

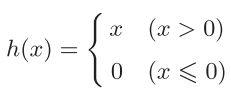
def relu(x):
    return np.maximum(0, x)
import numpy as np 
import matplotlib.pyplot as plt 

x = np.arange(-5, 5, 0.1)
y = relu(x)
plt.plot(x, y)
# plt.ylim()
plt.show()

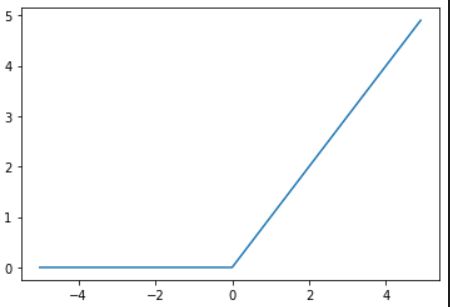
ReLU相比于传统的sigmoid函数，有3个作用：
1.防止梯度弥散
2.稀疏激活性
3.加快计算

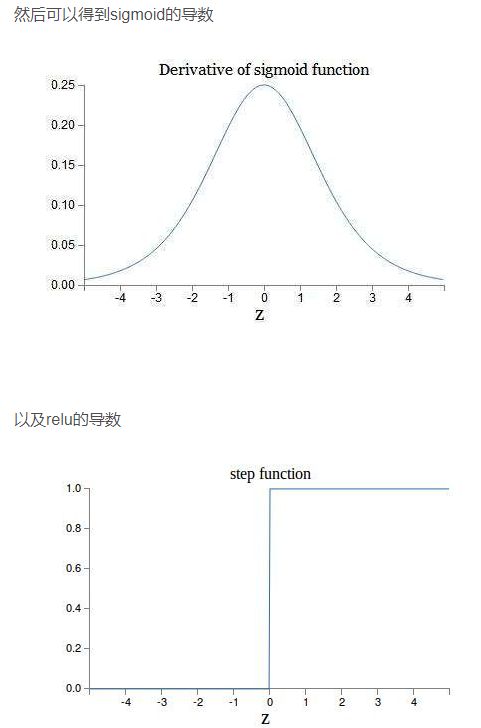
结论就是sigmoid的导数只有在0附近的时候有比较好的激活性，在正负饱和区的梯度都接近于0，所以这会造成梯度弥散，而relu函数在大于0的部分梯度为常数，所以不会产生梯度弥散现象。

第二，relu函数在负半区的导数为0 ，所以一旦神经元激活值进入负半区，那么梯度就会为0，也就是说这个神经元不会经历训练，即所谓的稀疏性。

第三，relu函数的导数计算更快，程序实现就是一个if-else语句，而sigmoid函数要进行浮点四则运算。综上，relu是一个非常优秀的激活函数

参考博客

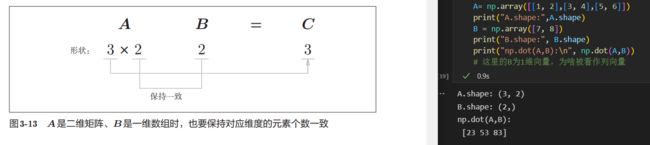
b.shape的结果是一个元组，一维数组的情况下也要返回和多维数组的情况下一致的结果

A=np.array([7, 8])
print(A.shape)
# (2,)

这里A是1维数组，看作列向量，所以形状为(2,),即有2行1列

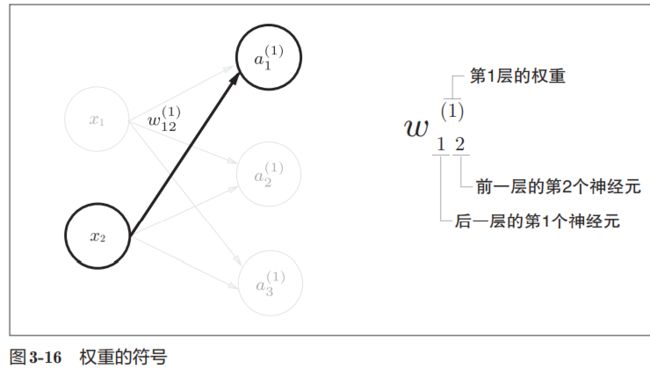
任何前一层的偏置神经元“1”都只有一个。偏置权重的数量取决于后一层的神经元的数量（不包括
后一层的偏置神经元“1”）。因为后一层的每个神经元都来自前一层的加权计算，而前一层的加权计算会对应不同的偏置神经元

代码实现上图的3层神经网络如下：

def init_network():
    # 进行权重和偏置的初始化，并保存在字典变量network中
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4],[0.2, 0.5],[0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3],[0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network

def forward(network, x):
    # 封装了将输入信号转换为输出信号的处理过程
    # forward表示的是从输入到输出方向的传递处理
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2 
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y 

network = init_network()
x = np.array([1, 0.5])
y = forward(network, x)
print(y)  #[0.31682708 0.69627909]

输出层的设计

神经网络可以用在分类和回归问题上，需要根据情况改变输出层的激活函数。

1. 回归问题 ------> 用恒等函数
2. 分类问题------>用softmax函数
   恒等函数会将输入按原样输出，对于输入的信息，不加任何改动地直接输出，所以在输出层使用恒等函数时，输入信号会原封不动地被输出。
   softmax函数：
   

def softmax(a):
    exp_a = np.exp(a)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y 

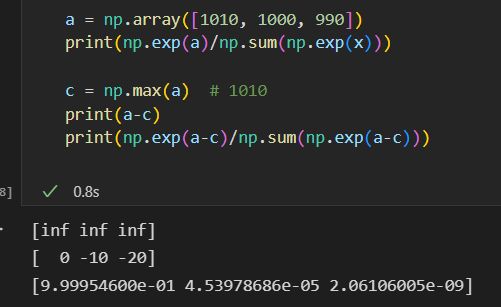
上面的softmax函数虽然正确表述了其数学表达式，但是在计算机的运算中容易溢出，笔记$e^{100}$会变成一个后面有40多个0的超大值。如果在这些超大值之间进行除法运算，结果会出现“不确定”的情况

综上，可以像下面这样实现softmax函数：

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c) # 溢出对策
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    return y 

一般而言，神经网络只把输出值最大的神经元对应的类别作为识别结果。即使使用softmax函数，输出值最大的神经元的位置也不会变。因此，神经网络在进行分类时，输出层的softmax函数可以省略。在实际的问题中，由于指数函数的运算需要一定的计算机运算量，因此输出层的softmax函数一般会被省略。

学习和推理

求解机器学习问题的步骤可以分为“学习”和“推理”两个阶段。
首先，在学习阶段进行模型的学习，然后，在推理阶段，用学到的模型对未知的数据进行推理（分类）。推理阶段一般会省略输出层的softmax函数。在输出层使用softmax函数是因为它和神经网络的学习有关系。

使用神经网络解决问题时，也需要先使用训练数据（学习数据）进行权重参数的学习；进行推理时，使用刚才学习到的参数，对输入数据进行分类。

Python有 pickle这个便利的功能。这个功能可以将程序运行中的对象保存为文件。如果加载保存过的 pickle文件，可以立刻复原之前程序运行中的对象。用于读入MNIST数据集的load_mnist()函数内部也使用了 pickle功能（在第 2次及以后读入时）。利用 pickle功能，可以高效地完成MNIST数据的准备工作。