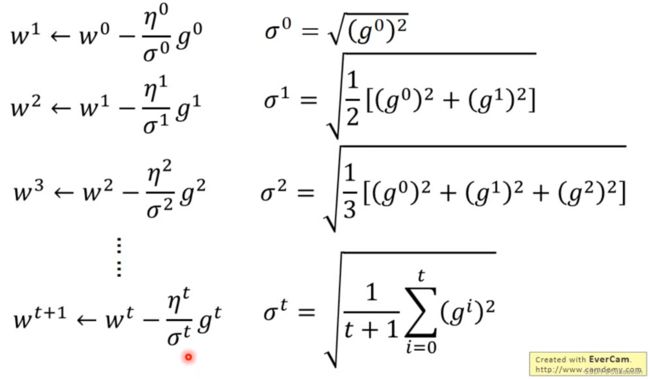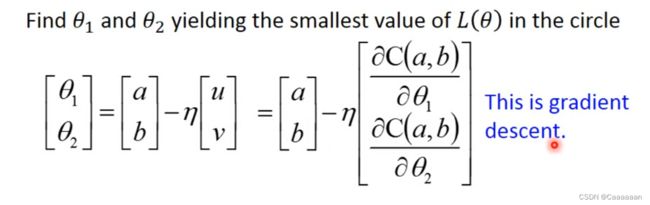梯度下降法
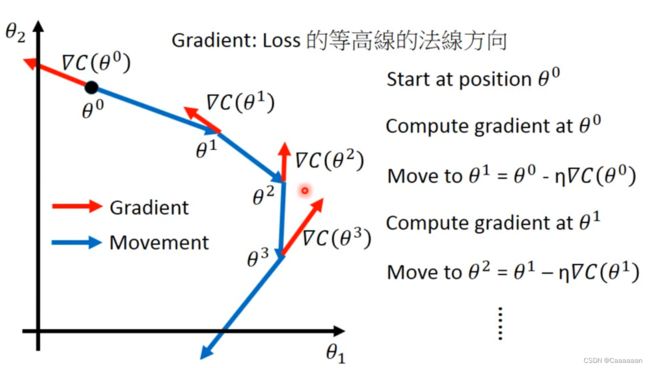
梯度下降
目的:解决优化问题——optimization problem
Tip1:调节学习率
——小心调节你的学习率
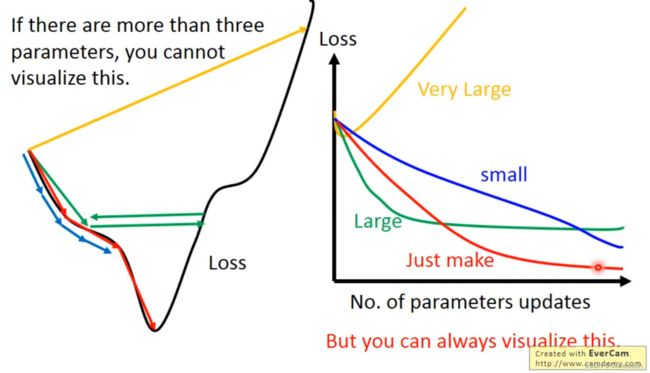
- 学习率太低——需要迭代次数比较大
- 学习率太高——错过最佳点,在最优点附近震荡
当你的参数(特征)高于三维时,我们没有办法观测到函数情况,进而进行学习率的调节
我们可以转换为观测——参数变化与Loss的变化
因此,在做梯度下降的时候,应该把参数变化与Loss函数的变化做出来
自适应学习率
——自适应学习率
一个简单的原理:学习率一定是越小越准确,虽然步子小,但是小步子一定能够到达最小值
基于原理:
- 每隔一些epochs之后,降低学习率
- 一开始的时候,我们假设离最佳点非常远,所以我们要用大步子去进行迈进
- 迈进几步之后呢,我们就离最佳点近了,这个时候,我们就降低我们的学习率,使得我们能够到达最佳点
Vanilla Gradient Descent
根据迭代次数 t的进行缩小的学习率
学习率是 t dependent的函数
η t = η t + 1 g t = ∂ L ( ω t ) ∂ ω ω t + 1 = ω t − η t g t \eta^t=\frac{\eta}{\sqrt{t+1}}\\ \\ g^t=\frac{\partial L(\omega^t)}{\partial\omega}\\ \\ \omega^{t+1}=\omega^t-\eta^tg^t\\ ηt=t+1ηgt=∂ω∂L(ωt)ωt+1=ωt−ηtgt
随着迭代次数越来越大,这个学习率就会越来越小
更好的方法是——实现“因材施教”
——Learning rate cannot be one-size-fits-all
——Giving different parameters different learning rates.
给与不同的参数不一样的学习率
Adagrad
- Divide the learning rate of each parameter by the root mean square of its previous derivatives.
将每个参数的学习率除以其先前导数的均方根。
ω t + 1 = ω t − η t σ t g t \omega^{t+1}=\omega^{t}-\frac{\eta^t}{\sigma^t}g^t ωt+1=ωt−σtηtgt
σ t \sigma^t σt ——过去 所有 微分值的均方根
η t = η t + 1 σ t = 1 t + 1 ∑ i = 0 t g ( i ) 2 \eta^t=\frac{\eta}{\sqrt{t+1}}\\ \sigma^t=\sqrt{\frac{1}{t+1}\sum^t_{i=0}g(i)^2}\\ ηt=t+1ησt=t+11i=0∑tg(i)2
因此两项相除得——
η t σ t = η ∑ i = 0 t g ( i ) 2 \frac{\eta^t}{\sigma^t}=\frac{\eta}{\sqrt{\sum_{i=0}^tg(i)^2}} σtηt=∑i=0tg(i)2η
因此得到Adagrad最后的迭代式子
ω t + 1 = ω t − η ∑ i = 0 t g ( i ) 2 g t \omega^{t+1}=\omega^t-\frac{\eta}{\sqrt{\sum_{i=0}^tg(i)^2}}g^t ωt+1=ωt−∑i=0tg(i)2ηgt
——Adagrad强调了一种反差的效果
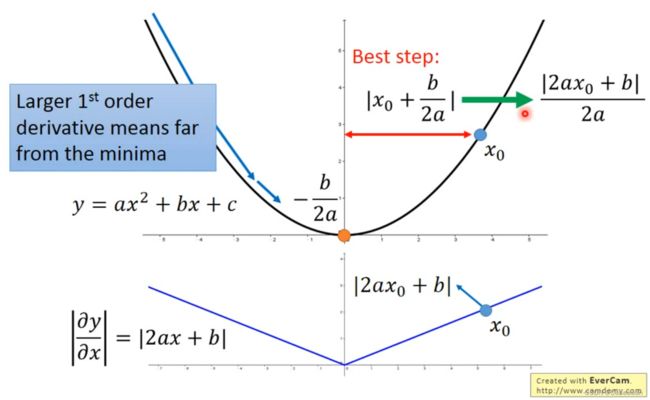
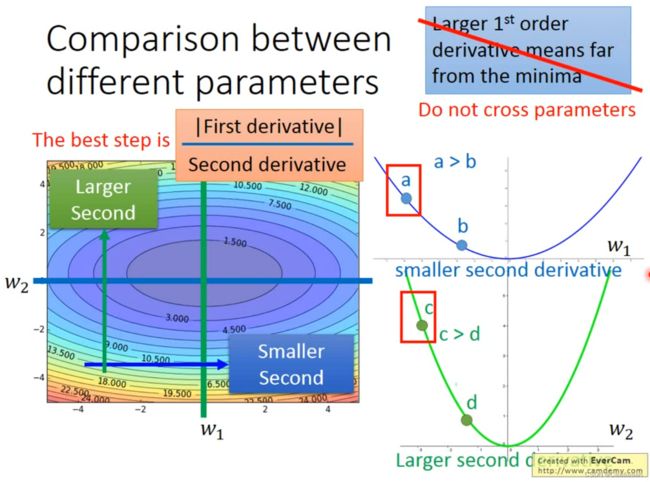
二次微分
当函数参数只有一个变量时,会发现,这里的微分越大,说明这个点离最低点(最优解)最远
如果有多个参数时,这个东西就不成立
——同时考虑多个参数,我们怎么思考这件事呢?
将二次微分考虑进来
我们需要将a点一次微分和二次微分的商和c点一次微分和二次微分的商,一同做考虑这件事
只有结合两次微分,才能真正反映,你当前所在的位置和最低点的距离
联系
在Adagrad里面呢
g t → ∣ F i r s t d e r i v a t i v e ∣ ∑ i = 0 t ( g i ) 2 → ∣ S e c o n d d e r i v a t i v e ∣ g^t\rightarrow |First\,\,\,derivative|\\ \sqrt{\sum_{i=0}^t(g^i)^2}\rightarrow |Second\,\,\,derivative| gt→∣Firstderivative∣i=0∑t(gi)2→∣Secondderivative∣
- 为什么需要用一次微分的均方根估算二次微分?
- 在数据量较大的环境下,计算二次微分的时间成本较大
- 能避免二次微分为0的情况吗???
Tip2: Stochastic Gradient Descent
能让你的Traning更快一点
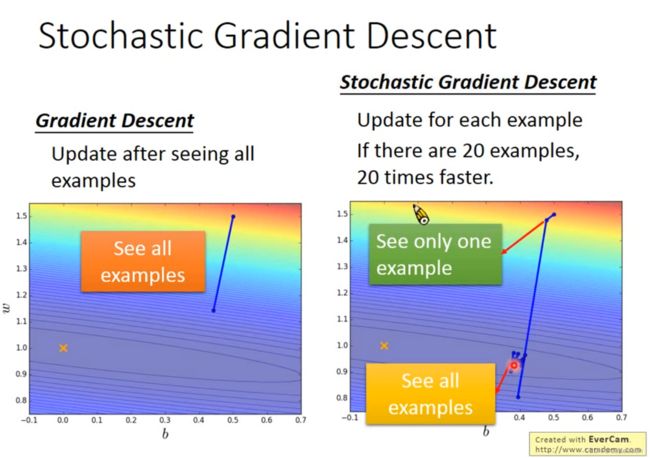
——原来的梯度下降在Loss Function里,考虑了所有的样本的误差值,梯度L也是考虑上了所有样本
——Stochastic的梯度下降呢,我们只考虑一个样本(随机或者按顺序采样),梯度也只计算这一单一样本,就将参数进行Update
——原始的梯度下降看完所有Example之后走了一步
——Stochastic的梯度下降,看完所有Example之后,走了样本数目这么多步
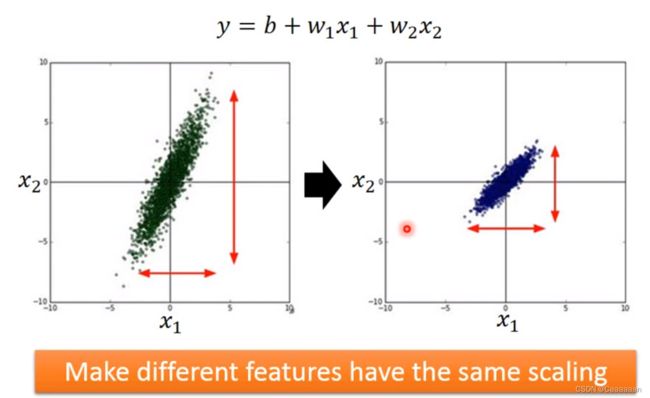
Tip3: 特征规约
——特征缩放
让考虑的特征拥有一样的度量
避免某个特征对预测的影响特别大
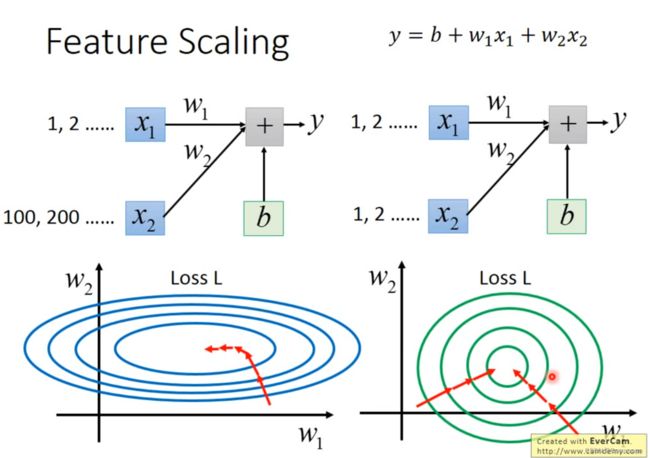
Why
对梯度下降有什么影响吗?
——长椭圆形状的error surface,在不进行AdaGrad的时候,你会比较难搞定他
——而进行了Scaling之后呢,error surface就呈现出正圆形的分布
——做完scaling之后呢,会使得梯度下降地比较有效率
How
——本质上是数据规范化的内容
数据预处理
方法一:
- 对于某一个维度的数据
- 求平均值 m i m_i mi
- 求标准差 σ i \sigma_i σi
v ′ = v − m i σ i v'=\frac{v-m_i}{\sigma_i} v′=σiv−mi
——做完这件事之后,你会发现,该维度的数据呈现正态分布
Warning of Maths
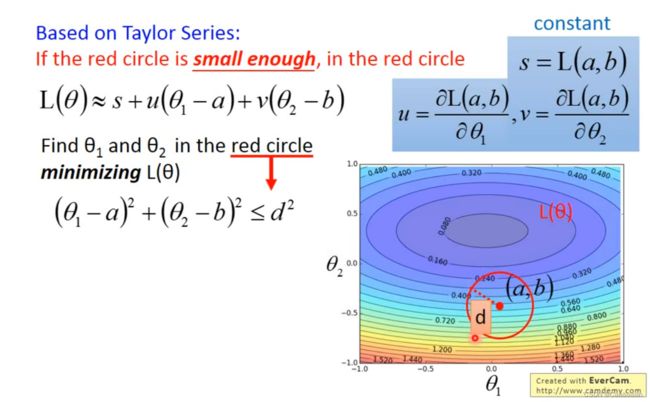
泰勒级数Review
h ( x ) = ∑ k = 0 ∞ h ( k ) ( x 0 ) k ! ( x − x 0 ) k = h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) + h ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . h(x)=\sum_{k=0}^\infty \frac{h^{(k)}(x_0)}{k!}(x-x_0)^k\\ =h(x_0)+h'(x_0)(x-x_0)+\frac{h''(x_0)}{2!}(x-x_0)^2+... h(x)=k=0∑∞k!h(k)(x0)(x−x0)k=h(x0)+h′(x0)(x−x0)+2!h′′(x0)(x−x0)2+...
当 x → x 0 x\rightarrow x_0 x→x0时, x − x 0 x-x_0 x−x0 就会比 ( x − x 0 ) 2 (x-x_0)^2 (x−x0)2大得多,我们就可以截断进行近似
h ( x ) ≈ h ( x 0 ) + h ′ ( x 0 ) ( x − x 0 ) h(x)\approx h(x_0)+h'(x_0)(x-x_0) h(x)≈h(x0)+h′(x0)(x−x0)
多变量的泰勒级数
h ( x , y ) = h ( x 0 , y 0 ) + ∂ h ( x 0 , y 0 ) ∂ x ( x − x 0 ) + ∂ h ( x 0 , y 0 ) ∂ y ( y − y 0 ) + . . . h(x,y)=h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0)+... h(x,y)=h(x0,y0)+∂x∂h(x0,y0)(x−x0)+∂y∂h(x0,y0)(y−y0)+...
后面接一些类似的二阶偏导等的式子
得近似值
h ( x , y ) ≈ h ( x 0 , y 0 ) + ∂ h ( x 0 , y 0 ) ∂ x ( x − x 0 ) + ∂ h ( x 0 , y 0 ) ∂ y ( y − y 0 ) h(x,y)\approx h(x_0,y_0)+\frac{\partial h(x_0,y_0)}{\partial x}(x-x_0)+\frac{\partial h(x_0,y_0)}{\partial y}(y-y_0) h(x,y)≈h(x0,y0)+∂x∂h(x0,y0)(x−x0)+∂y∂h(x0,y0)(y−y0)
形式推导
-
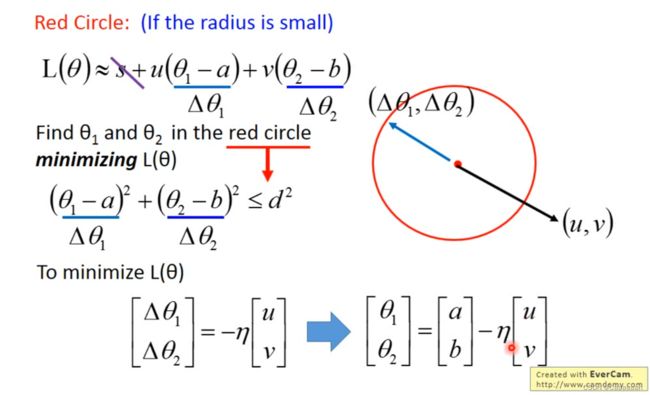
我们把 ( θ 1 − a ) (\theta_1-a) (θ1−a) 和 ( θ 2 − b ) (\theta_2-b) (θ2−b) 当作 Δ θ 1 \Delta\theta_1 Δθ1 和 Δ θ 2 \Delta\theta_2 Δθ2
-
就相当于,在这个Circle里面,存在一个 v e c t o r ( Δ θ 1 , Δ θ 2 ) vector(\Delta\theta_1 ,\Delta\theta_2 ) vector(Δθ1,Δθ2)和 v e c t o r ( u , v ) vector(u,v) vector(u,v)做内积,使得 L ( θ ) L(\theta) L(θ)最小
-
那么这个 ( Δ θ 1 , Δ θ 2 ) (\Delta\theta_1 ,\Delta\theta_2 ) (Δθ1,Δθ2)和 ( u , v ) (u,v) (u,v) 反向,而且长度在circle极限
——最后得到的式子,实质上就是梯度下降
——但这个式子的前提是,泰勒级数给我们的估计是足够精确的
——只有当上图的red circle足够小的时候,才有这样的式子成立
同时呢,我们的学习率 η \eta η 和 半径 是成正比的,因此学习率不能太大
——因此,理论上,我们的学习率需要无穷小的情况下,才会有这样的式子成立;虽然实操上,只要足够小就可以
——因此,理论上,提出通过增加泰勒式子的二次式,这样我们的学习率可以稍微设置大一点
但是在实际上,我们会增加很多运算,增加二次微分,增加Hession matrix和Hession matrix的逆等等,因此在deep learning并没有那么的使用
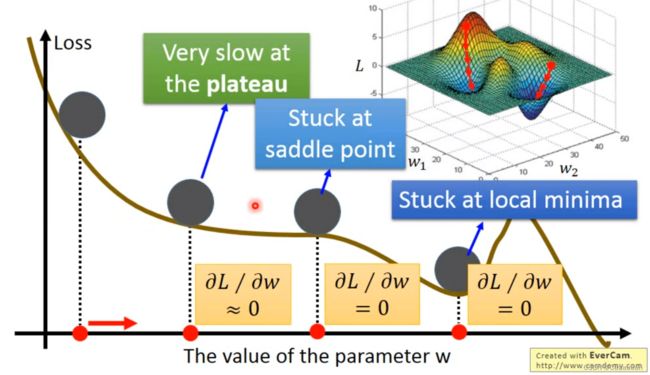
梯度下降法的限制
- 只能找到局部最优,寻找不到全局最优
- 有可能卡在不是最优点,卡在微分值为0的位置
- 或者微分值算出来很小,存在误差,但这里卡住了
——为什么我的梯度下降,Loss Function不降反升呢?
有可能处于的位置是:
- 前面比较矮,右边也比较矮
- 这个时候,程序会往右前方进去
- 但是,右前方是个梯度升高的地方