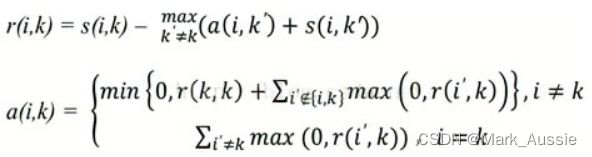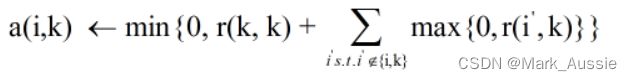Affinity Propagation (AP)近邻传播聚类
近邻传播聚类:根据 N 个数据点之间的相似度聚类,相似度可以是对称的,即两个数据点互相之间的相似度一样(如欧氏距离);也可以是不对称的,即两个数据点互相之间的相似度不等。这些相似度组成 N×N 的相似度矩阵 S (N代表N个数据点)。
不需要事先指定聚类数目,将所有的数据点都作为潜在的聚类中心,称为 exemplar。
以 S 矩阵的对角线上的数值s (k, k)作为 k 点能否成为聚类中心的评判标准,该值越大,这个点成为聚类中心的可能性越大,称为参考度 p ( preference) 。聚类的数量受到参考度 p 的影响,如果每个数据点都有可能作为聚类中心,则 p 取相同的值。如果取输入的相似度的均值作为 p 的值,聚类数量是中等的;如果取最小值,得到较少的聚类。
AP算法传递的两种消息类型,responsibility 和 availability;r(i,k) 表示从点 i 发送到候选聚类中心 k的数值消息,反映 k 点是否适合作为 i 点的聚类中心。a(i,k) 则从候选聚类中心 k 发送到 i 的数值消息,代表 i 点是否选择 k 作聚类中心。
r (i, k)与a (i, k)越强,则 k 点作为聚类中心的可能性就越大,且 i 点属于 k 点的可能性也越大。
AP算法不断更新每个点的吸引度和归属度,直到产生m个高质量的exemplar,同时将其余的数据点分配到相应的聚类中。
名词解释:
exemplar:聚类中心。
similarity:点 i 和 j 的相似度,记为S(i,j)。j 为 i 的聚类中心的相似度。
preference:点 i 的参考度称为 P(i) 或 S(i,i)。点 i 作为聚类中心的参考度。可取S相似度中值。
responsibility:r(i,k) 代表点 k 适合作为点 i 的聚类中心的程度。
availability:a(i,k) 描述点 i 选择点 k 作为其聚类中心的适合程度。
damping factor:阻尼系数,主要是起收敛作用的。防止数据震荡,引入地衰减系数,每个信息值等于前一次迭代更新的信息值的λ倍加上此轮更新值得1-λ倍,其中λ在0-1之间,默认为0.5。
AP聚类算法将每个数据看成图中的一个节点,迭代的过程是在图中通过传播信息找到聚类集合。计算两个数据点的相似度采用距离的负数,此时距离越近,相似度越大。
相似矩阵S中 i 到 j 的相似度就是距离的负数。但是主对角线上的那些数表示的是某个点和自身的相似度,根据算法要求,主对角线上的值s(k,k)一般称为偏向参数,通常对所有 k,s(k,k) 都是相等(是其自身),取非主对角线上的所有数的中位数(其大小与最后得到的类的数目有关,通常这个数越大,得到的类的数目就越多)。
如此设定可能是因为AP聚类算法是要用图论理解,把所有的点都看成一个图中的节点,通过节点之间的信息传递来达到聚类的效果。
聚类就是个不断迭代的过程,迭代的过程主要更新两个矩阵,
代表(Responsibility)矩阵R = [r(i,k)]N×N 和适选 (Availabilities)矩阵A=[a(i,k)]N×N。
这两个矩阵初始化为0,N是所有样本的数目。
r(i,k)表示第k个样本适合作为第i个样本的类代表点的代表程度,
a(i,k)表示第i个样本选择第k个样本作为类代表样本的适合程度。
每次更新后就可以确定当前样本 i 的代表样本(exemplar)点k,k 是使 {a(i,k)+r(i,k)} 取得最大值的那个k 点,如果 i=k,代表样本 i 就是这个簇的类代表点。
迭代停止的条件就是所有的样本的所属都不在变化为止,或者迭代了n次没有变化(n 自定义)。
还有一种判断点属于哪一类的方法,找出所有决策矩阵主对角线元素 {a(k,k)+r(k,k)} 大于 0 的所有点,这些点全部都是类代表点,之后在决定其余的点属于这里面的一类。
AP聚类算法迭代过程很容易产生震荡,因此每次迭代都加上一个阻尼系数 λ。
公式解释:
a(i,k’) 表示除 k外,其他点对 i 点的归属度值,初始为0;
s(i,k’) 表示除 k 外,其他点对 i 的吸引度,即 i 外其他点都在争夺 i 点的 所有权;
r(i,k)表示点 k 成为点 i 的聚类中心的累积证明,r(i,k)值大于0 表示点 k 成为聚类中心的能力强。
此时只考虑哪个点 k 成为点 i 的聚类中心的可能性最大,但是没考虑这个吸引度最大的 k 是否也经常成为其他点的聚类中心(即归属度),若点 k 只是点 i 的聚类中心,不是其他任何点的聚类中心,则会造成最终聚类中心个数大于实际的中心个数。
a(i,k):归属度信息,表示点 i 选择点 k 为其聚类中心的合适程度;
r(i’,k) 表示点 k 作为除 i 外其他点的聚类中心的相似度值,取所有大于等于0的吸引度值,加上k作为聚类中心的可能程。即点 k 在这些吸引度值大于 0 的点的支持下,点 i 选 k 为中心的累积证明。
注:算法复杂度较高,为O(N*N*logN),而K-Means只是O(N*K)的复杂度。当N较大时(N>3000),
AP聚类算法往往需要算很久。
若以误差平方和衡量优劣,AP聚类比其他方法的误差平方和都低。
AP通过输入相似度矩阵来启动算法,允许数据呈非欧拉分布,及非常规的点-点度量方法。
参考:
AP近邻传播聚类算法(Affinity Propagation)_船长工作室的博客-CSDN博客
Affinity Propagation: AP聚类算法_winkake的博客-CSDN博客
迭代更新说明:近邻传播 Affinity Propagation(AP) 聚类算法原理及实现_scott198510的博客-CSDN博客_ap近邻传播聚类算法