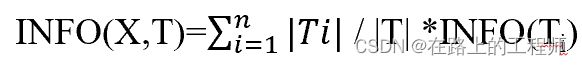决策树主要原理
决策树
决策树的概念
1、决策树是一种分类器,是一个有向、无环树。
2、树中根节点没有父节点,一个节点可以有1-2个或者没有子节点。
3、每个叶节点都对应一个类别标识C的值;每个内部节点都对应一个用于分割数据集的属性Xi,称为分割属性;每个内部节点都有一个分割判断规则qj。
决策树原理
1、决策树原理:归纳推理
2、归纳:是从特殊到一般的过程
3、归纳推理:从若干个事实表现出的特征、特性或属性中,通过比较、总结、概括而得出一个规律性的结论。
4、归纳推理的基本假定:任一假设如果能在足够大的训练样本集中很好地逼近目标函数,则它也能在未见样本中很好地逼近目标函数。
ID3算法
Quinlan设计的ID3方法是国际上最有影响和最为典型的决策树学习方法。在ID3方法中, Quinlan使用信息增益度量选择测试属性。
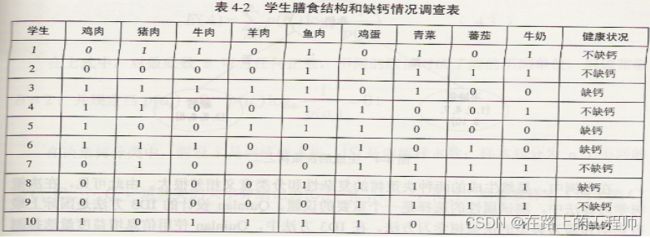
举例说明测试属性选择的重要性:假设卫生部门调查学生的膳食结构和缺钙之间的关系,得调查数据如下表所示,其中1表示主要膳食包含事务,0表示主要膳食不包含该食物。
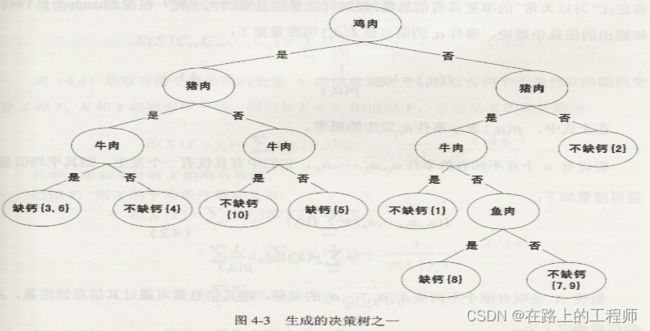
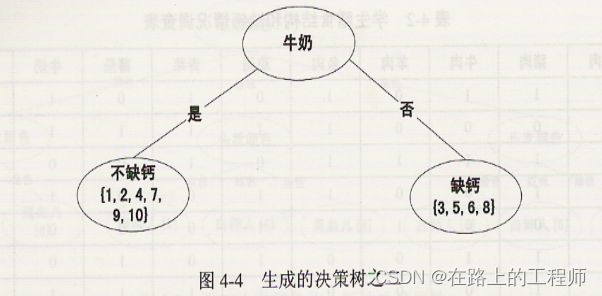
对于不同的测试属性及其先后顺序将会产生不同的决策树,下面是产生的两个不同的决策树。
从中可以看出两个决策树差别巨大,因此测试属性的选择十分重要。ID3中使用信息增益选择测试属性。
信息的度量
信息量的大小取决于信息内容消除的人们认识的不确定程度,消除的不确定程度大,则发出的信息量就大;消除的不确定程度小,则发出的信息量就越小。
信息消除的人们认识上“不确定程度”的大小,就是该信息所包含信息量的大小。
例如,现在某甲到1000人的学校去找某乙,这时,在某甲的头脑中,某乙所处的可能性空间是该学校的1000人。当传达室告诉他:“这个人就在管理系”,而管理系就100人,那么他获得的信息为100/1000=1/10,也就是说可能性空间缩小到原来的1/10。通常,我们不直接用1/10表示信息量,而用1/10的负对数来表示,即-log1/10=log10。
如果管理系的人告诉他,某乙就在管理系的教研室,那么他获得了第二个信息。假定管理系教研室有10个教师,则第二个信息的确定性又缩小到原来的100/1000*10/100=10/1000。显然:-log100/1000+(-log10/100)=-log10/1000。
只要可能性范围缩小了,获得的信息量总是正的;如果可能性范围没有变化。-log1=0,获得的信息量就是零;如果可能性范围扩大了,信息量变为负值,人们对这件事的认识变得更模糊了。
信息量的计算方式
我们利用概率来度量信息。信息量的单位为比特(bit)。信息量的公式为:
一比特信息量指含有两个独立均等概率状态的事件所具有的不确定性能被全部消除所需要的信息。这里的Xi代表第i个状态,P(Xi)代表出现第i个状态的概率,H(X)就是用以消除这个系统不确定性所需的信息量。
例如,硬币下落可能有正反两种状态,出现这两种状态的概率都是1/2,即:P(Xi)=0.5,这时,H(x)=-[P(X1)log2P(X1)+P(X2)log2P(X2)]=-(-0.5-0.5)=1比特。
同理可得,投掷均匀正六面体骰子的H(X)=2.58比特。
注:计算信息量这一公式恰好与热力学第二定律中熵的公式相一致,熵是系统无序状态的度量,即系统不确定性的度量。但是,信息量和熵所反应的系统运动过程和方向相反。系统的信息量增加总是表明不确定性减少,有序化程度增大。因此,信息在系统的运动过程中可以看作是负熵。信息量越大,则负熵越大。熵值越小,反映了该系统无序程度越小,有序化越高。信息度量表述了系统的有序化过程。
ID3算法的一些定义
定义4-2:若某属性存在n个相同的概率的状态,则每个状态的概率p是1/n,一个消息可以消除状态出现的不确定性,该消息传递的信息量为-log2(p)=log2(n)
定义4-3:若给定的某属性概率分布P=(p1,p2,…,pm),一个消息可以消除该属性状态出现的不确定性,则该消息传递的信息量称为P的熵,即:
I(P)=-(p1*log2(p1)+…+pm*log2(pm))(就是信息的定义公式)
定义4-4:若一个记录的集合T根据类别属性的值分成相互独立的类c1,...,ck,则识别T的一个元素(元组)所属哪个类所需要的信息量是info(T)=I§,其中P是(c1,c2…ck)的概率分布,即P=(|c1|/|T|,……,|ck|/|T|)。
定义4-5:若我们先根据非类别属性X的值将T分成集合T1,T2…Tn,则确定T中的一个元素所属类的信息量可通过确定Ti的加权平均值来得到,即Info(Ti)的加权平均为:
定义4-6:将增益Gain(X,T)定义为:Gain(X,T)=Info(T)-Info(X,T),即增益的定义是两个信息量之间的差值。
理解:不知任何信息时确定一个元素属于那类所需全部信息量为Info(T),知道一个属性信息后,确定一个元素属于那类所需全部信息量为Info(X,T), Info(X,T) 越小说明属性X对于分类越重要(即很小的信息量就分出该元素属于那类了,注意:事情的不确定性越大,要搞清楚这件事就需要越大的信息量。),所以Gain(X,T)值越大说明Info(X,T)越小。
ID3算法计算每个属性的信息增益。具有最高信息增益的属性选作给定的集合T的测试属性。创建一个节点,并以该属性标记,对属性的每个值创建分支,并据此划分样本。
例题
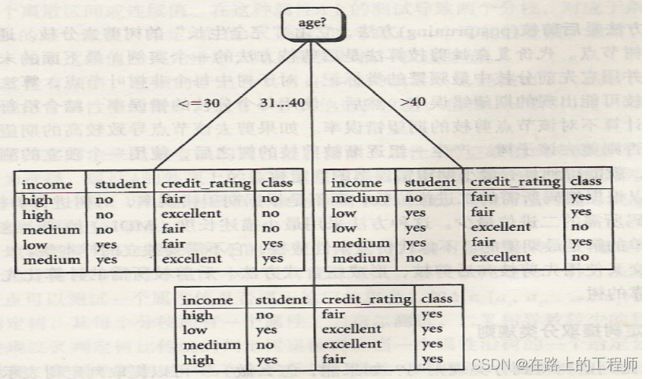
下表给出了取自AllElectronics顾客数据库元组训练集。类标号属性buys_computer有两个不同的值(yes,no)。设类C1对应yes,而类C2对应no。类yes有9个样本,类no有5个样本。给定样本分类所需要的期望信息为
| RID | age | income | student | credit_rating | Class: buys_computer |
|---|---|---|---|---|---|
| 1 | <=30 | high | no | fair | no |
| 2 | <=30 | high | no | excellent | no |
| 3 | 31…40 | high | no | fair | yes |
| 4 | >40 | medium | no | fair | yes |
| 5 | >40 | low | yes | fair | yes |
| 6 | >40 | low | yes | excellent | no |
| 7 | 31…40 | low | yes | excellent | yes |
| 8 | <=30 | medium | no | fair | no |
| 9 | <=30 | low | yes | fair | yes |
| 10 | >40 | medium | yes | fair | yes |
| 11 | <=30 | medium | yes | excellent | yes |
| 12 | 31…40 | medium | no | excellent | yes |
| 13 | 31…40 | high | yes | fair | yes |
| 14 | >40 | medium | no | excellent | no |
C1 = 9/14, C2 = 5/14
info(T) = I(P) = I(C1, C2) = -9/14log2(9/14)-5/14log2(5/14)=0.940
下一步,需要计算每个属性的熵。从age开始。需要观察每个样本值的yes和no分布。
我们对每个分布计算期望信息
针对age属性,按照<30、31…40、>40三个区间划分,将整个数据集T划分成了T1、T2、T3三个集合(注意,不是三个独立的类别),所以这里面需要用到定义5。
age < 30(T1集合): info(T1)=I(C1, C2) = -2/5log2 (2/5)-3/5log2 (3/5)=0.971
age=31…40(T2集合): info(T2)=I(C1, C2) = 0 ,因为全部都是C1类,相当于是不需要信息。
age>40(T3集合): info(T3)=I(C1, C2) = 0.971(与T1相同,都是3个C1和2个C2)
所以根据样本age划分,对一个给定的样本分类所需的期望信息为:
info(age, T) = 5/14*0.971 + 4/14*0 + 5/14*0.971 = 0.694
Gain(age, T) = info(T) - info(age, T) = 0.246
类似可以计算出
Gain(income)=0.029,Gain(student)=0.151,Gain(credit_rating)=0.048
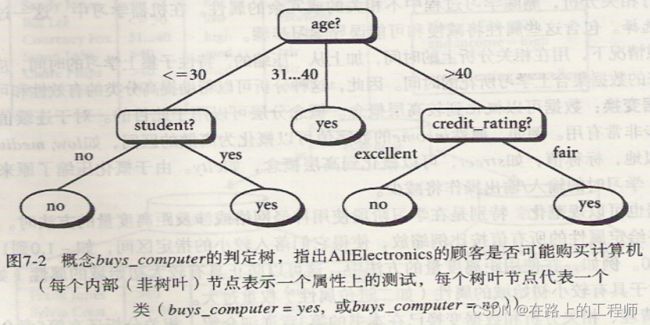
最终的决策树如下:
剪枝
-
剪枝的原因:过度匹配(将异常数据也进行分类了)、树太深。
-
剪枝的目的:删除由于噪声数据而引起的分支,从而避免决策树的过匹配;使树更易理解。
-
剪枝方法分类:
预剪枝:在生成决策树时,按给定阈值停止生成分枝,停止处的节点为叶子节点,该叶子节点只包含子集中最多的一类元素;
后剪枝:在生成完整决策树后,按分枝分类的错误率进行剪枝,剪去分支用叶子节点代替,树叶用被代替的子树中最频繁的类来标记。
-
剪枝方法
预剪枝方法:预先设定树的深度,以便生成树一边判断是否超过深度,超过就不再生成。 后剪枝方法:决策树生成完后,根据规则(判断预测的准确性)再剪枝。