【滤波跟踪】基于UKF与KF实现单目标无杂波环境下二维雷达量测的目标跟踪算法附matlab代码
1 内容介绍
随着科技的发展,雷达对目标跟踪的精确度要求越来越高.但在实际应用中,系统所处的环境会受到各种各样的干扰,此时,卡尔曼滤波器凭借其优良的噪声处理能力而被应用到各种领域,是现阶段雷达跟踪中最常用的算法.文章在卡尔曼滤波算法的基础上,就如何将其应用于雷达目标跟踪系统的问题进行了研究与仿真;分析了卡尔曼滤波与常增益滤波的适用范围及优缺点;给出了极坐标系下卡尔曼滤波的计算及过程噪声方差的获取方法;最后以目标仿真结果证明了估计的有效性.文章定性、定量地对卡尔曼滤波在雷达单目标跟踪算法中的应用情况进行了分析,明确指出了算法的优良性能及局限性,实际应用时也可以对目标进行分段处理.该算法可直接应用于某些单目标跟踪系统,或与其他算法结合,用于多目标跟踪系统,如道路监测雷达系统等.
2 部分代码
dbstop if error
%% 两坐标雷达带Doppler量测的UKF目标跟踪
clc
clear all
close all
%% 1.基本参数与模型
Ts=0.5;
% Nstep=80; % total dynamic steps
Nstep=240;
totalTime=Ts*Nstep; %总时长
sigma_r=0.6; %量测噪声的标准差 距离
sigma_theta=0.1; %量测噪声的标准差 角度
sigma_vr=0.02; %量测噪声的标准差 多普勒速度
sigma_q=0.5; %过程噪声的标准差
nx=4;
%------过程噪声的分布矩阵-----------------
Gamma=[ Ts*Ts/2, 0;
Ts, 0;
0, Ts*Ts/2;
0, Ts]; % 扰动矩阵或者说是过程噪声的分布矩阵
Q0=[sigma_q^2,0;0,sigma_q^2]; % 过程噪声的协方差矩阵
Q=Gamma*Q0*Gamma';
f=@(x)[
x(1)+Ts*x(2);
x(2);
x(3)+Ts*x(4);
x(4)
]; % nonlinear state equations
h=@(x)[
x(1);
x(3);
];
% R=[ sigma_r^2, 0, 0;
% 0, sigma_theta^2, 0;
% 0, 0, sigma_vr^2 ]; %量测噪声的协方差矩阵 因为量测方程是建立在极坐标系下的,所以不存在转换量测
% r=0.7; %std of measurement
% Q=sigma_q^2*eye(nx); % covariance of process
% R=r^2; % covariance of measurement
save ('Basic_arguments.mat', 'Ts','Nstep','totalTime', 'sigma_r', 'sigma_theta','sigma_vr', 'sigma_q', 'f', 'Gamma', 'Q', 'h');
% 补充 传统KF 参数
sigma_r=0.5;
F=[1,Ts,0,0;0,1,0,0;0,0,1,Ts;0,0,0,1];
H=[1,0,0,0;0,0,1,0];
% R_kf=[sigma_r^2,0;0,sigma_r^2];
%% 2.模拟运动目标并产生量测数据
% 2.1 直线运动
Target1_info = object_model_1(-300, 400, 15, 0, 0);
% 2.2 目标量测值
[Z_polar,Z_Rt] = Measure_rdps(Target1_info);
Xe_ukf = zeros(nx,Nstep); %estmate % allocate memory 滤波输出的结果集合
Xe_kf = zeros(nx,Nstep); %estmate % allocate memory 滤波输出的结果集合
%% 3.跟踪
% 3.1 初始化
x_ukf=[Z_Rt(1,2) (Z_Rt(1,2)-Z_Rt(1,1))/Ts Z_Rt(2,2) (Z_Rt(2,2)-Z_Rt(2,1))/Ts]'; % 初始时以量测值作为滤波值
x_kf=x_ukf;
Xe_ukf(:,1) = x_ukf;Xe_ukf(:,2) = x_ukf; % 滤波输出的结果集合
Xe_kf(:,1) = x_ukf;Xe_kf(:,2) = x_ukf; % 滤波输出的结果集合
[R,P0]=calRP(Z_polar(:,2));
P=P0;
% P = eye(nx); % initial state covraiance
% P_kf=[sigma_r^2, sigma_r^2/Ts, 0, 0; %起始的滤波误差协方差
% sigma_r^2/Ts,2*sigma_r^2/(Ts^2)+Ts^2*sigma_q^2/4, 0, 0;
% 0, 0, sigma_r^2, sigma_r^2/Ts;
% 0, 0, sigma_r^2/Ts, 2*sigma_r^2/(Ts^2)+Ts^2*sigma_q^2/4];
% 3.2 UKF
for k=3:Nstep
% 0.实时计算噪声协方差矩阵
[R,~]=calRP(Z_polar(:,k));
% 1.UKF 直角坐标系
[x_ukf, P] = ukf(f,x_ukf,P,h,Z_Rt(:,k),Q,R); % ukf
Xe_ukf(:,k) = x_ukf; % save estimate
% 2.KF 直角坐标系
[x_kf,P]=kalman_filter(x_kf,P,F,Gamma,Q0,H,R,Z_Rt(:,k)); % ukf
Xe_kf(:,k) = x_kf; % save estimate
end
%% 4.结果分析
figure;
axis equal;
% axis([-400 400 300 500])
hold on;
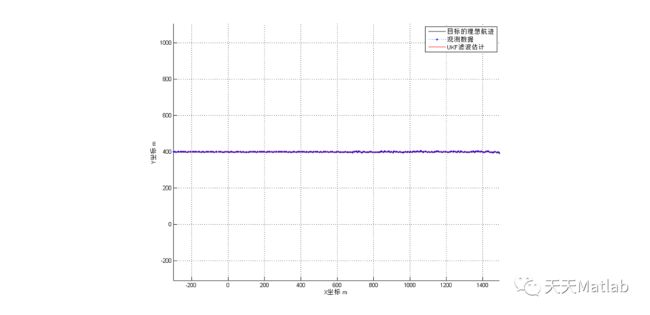
plot(Target1_info(1,:),Target1_info(3,:),'k','LineWidth',1.1);
plot(Z_Rt(1,:),Z_Rt(2,:),':.b');
plot(Xe_ukf(1,:),Xe_ukf(3,:),'r');
legend('目标的理想航迹','观测数据','UKF滤波估计');
axis equal;
hold off;
xlabel('X坐标 m')
ylabel('Y坐标 m')
grid on;
figure;
axis equal;
% axis([-400 400 300 500])
hold on;
plot(Target1_info(1,:),Target1_info(3,:),'k','LineWidth',1.1);
plot(Z_Rt(1,:),Z_Rt(2,:),':.b');
plot(Xe_kf(1,:),Xe_kf(3,:),'r');
legend('目标的理想航迹','观测数据','KF滤波估计');
axis equal;
hold off;
xlabel('X坐标 m')
ylabel('Y坐标 m')
grid on;
3 运行结果
4 参考文献
[1]孟凡彬. 基于随机集理论的多目标跟踪技术研究[D]. 哈尔滨工程大学.
[2]李珂, 王瑞, 宋建强. 基于卡尔曼滤波的雷达单目标跟踪算法研究[J]. 空间电子技术, 2019, 016(001):16-20.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机、雷达通信、无线传感器等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。