论文阅读《COMPLETER: Incomplete Multi-view Clustering via Contrastive Prediction》

---

论文信息

论文标题：COMPLETER: Incomplete Multi-view Clustering via Contrastive Prediction
论文作者：Yijie Lin, Yuanbiao Gou, Zitao Liu, Boyun Li, Jiancheng Lv, Xi Peng
论文来源： 2021，CVPR
论文地址：download
论文代码：download

---

一、Abstract

本文研究了不完全多视图聚类分析中两个具有挑战性的问题，i）如何在没有标签的帮助下学习不同视图之间的信息性和一致性表示，ii）如何从数据中恢复缺失的视图。
本文提出了一个新的目标，即从信息论的角度将表示学习和数据恢复整合到一个统一的框架中。具体来说，通过对比学习最大化不同视图之间的互信息来学习信息丰富的一致表示，通过双重预测最小化不同视图的条件熵来恢复缺失的视图。

本文所指的数据恢复是面向任务的，即只恢复共享的信息而不是所有的信息，以便于MVC等下游任务的完成。

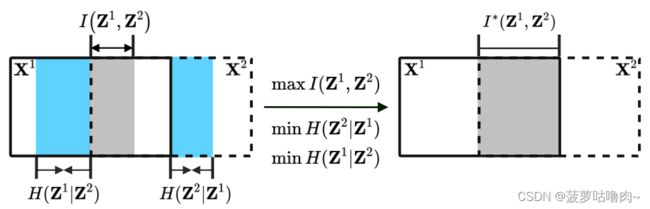
实线和虚线矩阵分别表示视图1$(X^1)$和视图2$(X^2)$中包含的信息。
互信息$I(Z^1,Z^2)$（灰色区域），量化了$Z^1$和$Z^2$共享的信息量，其中$Z^1$和$Z^2$分别是$X^1$和$X^1$的表示。【为了学习一致的表示，最大化互信息】
条件熵$H(Z^i|Z^j)$（蓝色区域）最小化，这将鼓励恢复丢失的视图，因为当且仅当$H(Z^i|Z^j)=0$时，$Z^i$完全由$Z^j$确定，其中i=1，j=2或i=2，j=1。
一方面，$I(Z^1,Z^2)$的最大化可以增加共享信息的数量，从而提高数据的可恢复性，即更容易从一个视图恢复到另一个视图。另一方面，当$H(Z^i|Z^j)$量化以$Z^j$为条件的$Z^i$的信息量时，$H(Z^i|Z^j)$的最小化将鼓励丢弃不同视图之间的不一致信息，从而进一步提高一致性。

二、Introduction

1.一些研究表明：对比学习的成功可以归因于互信息的最大化。
2.不一致性可以用条件熵来定义，而缺失的数据可以通过最小化不一致性来恢复。

三、The Proposed Method（COMPLETER）

对比预测的不完全多视图聚类（COMPLETER）

（一）整体框架

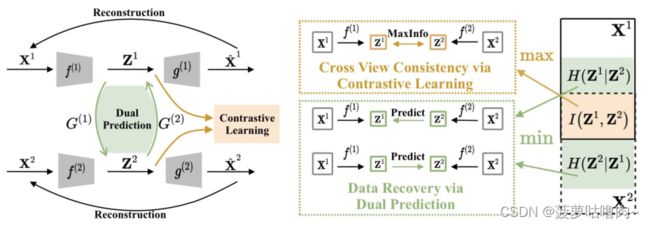
方法包含三个联合学习目标，即视图内重建、跨视图对比学习和跨视图双重预测。具体而言，视图内重建目标旨在以最小的重建损失将所有视图投影到视图特定的空间中。通过最大化$Z^1$和$Z^2$之间的互信息来实现跨视角对比学习目标。交叉视图双重预测目标通过最小化条件熵$H(Z^i|Z^j)$，利用两个映射$G^{(1)}$和$G^{(2)}$从另一个视图恢复一个视图。

（二）目标函数

以双视图数据为例。给定n个实例的数据集，$\overline{\mathbf{X}}=\left\{{\overline{\mathbf{X}}}^{1,2},{\overline{\mathbf{X}}}^1,{\overline{\mathbf{X}}}^2\right\}$，其中${\overline{\mathbf{X}}}^{1,2},{\overline{\mathbf{X}}}^1,{\overline{\mathbf{X}}}^2$分别表示examples presented in both views，the first view only，and the second view only。
m为${\overline{\mathbf{X}}}^{1,2}$的完整examples的数据大小。
$$\mathcal{L}={\mathcal{L}}_{cl}+{\lambda }_1{\mathcal{L}}_{pre}+{\lambda }_2{\mathcal{L}}_{rec}$$

1.视图内重建

对于每个视图，我们将其通过自动编码器，通过最小化来学习潜在表示$Z^v$。
$${\mathcal{L}}_{rec}=\sum _{v=1}^2\sum _{t=1}^m{\Vert {\mathbf{X}}_t^v-g^{(v)}\left(f^{(v)}\left({\mathbf{X}}_t^v\right)\right)\Vert }_2^2$$
$X_t^v$表示$X^v$的第t个样本。
$f^{(v)}、g^{(v)}$表示第v视图的编码器和解码器。因此，第v视图中第t个样本的表示如下所示：
$${\mathbf{Z}}_t^v=f^{(v)}(X_t^v)$$

2.跨视图对比学习

在${\mathcal{L}}_{rec}$参数化的潜在空间中，我们进行对比学习，学习不同视图之间的共同表示。
$${\mathcal{L}}_{cl}=-\sum _{t=1}^m\left(I\left({\mathbf{Z}}_t^1,{\mathbf{Z}}_t^2\right)+\alpha \left(H\left({\mathbf{Z}}_t^1\right)+H\left({\mathbf{Z}}_t^2\right)\right)\right)$$

从信息论来看，信息熵是一个事件所传递的平均信息量。因此更大的熵$H(Z^i)$表示信息更丰富的表示$Z_i$。
另一方面，$H(Z^1)$和$H(Z^2)$的最大化将避免将所有样本分配给同一个簇。

---

为了表示$I\left({\mathbf{Z}}_t^1,{\mathbf{Z}}_t^2\right)$，我们首先定义变量$z$和$z^{\prime }$的联合概率分布$\mathcal{P}\left(z,z^{\prime }\right)$。由于softmax函数堆叠在编码器的最后一层，$Z_1$和$Z_2$的每个元素都可以被视为超簇类概率。换句话说，$Z_1$和$Z_2$可以理解为两个离散的cluster分配变量z和$z^{\prime }$在D“类”上的分布，其中D是$Z_1$和$Z_2$的维数。因此，$\mathcal{P}\left(z,z^{\prime }\right)$被定义为$P\in {\mathcal{R}}^{D\times D}$，$i.e.$,
$$\mathbf{P}=\frac{1}{m}\sum _{t=1}^m{\mathbf{Z}}_t^1{\left({\mathbf{Z}}_t^2\right)}^{\top }$$
${\mathbf{P}}_d$和${\mathbf{P}}_d^{\prime }$表示边际概率分布$\mathcal{P}(z=d)$和$\mathcal{P}(z=d^{\prime })$，它们可以通过对联合概率分布矩阵$\mathbf{P}$的第$d$行和第$d^{\prime }$列求和得到。
对于离散分布：
$${\mathcal{L}}_{cl}=-\sum _{d=1}^D\sum _{d^{\prime }=1}^D{\mathbf{P}}_{d{d}^{\prime }}\ln \frac{{\mathbf{P}}_{d{d}^{\prime }}}{{\mathbf{P}}_d^{\alpha +1}\cdot {\mathbf{P}}_{d^{\prime }}^{\alpha +1}}$$
${\mathbf{P}}_{d{d}^{\prime }}$是P的第d行和第d′列的元素，α是熵的平衡参数。

3.跨视图双重预测

$H\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)=-{\mathbb{E}}_{{\mathcal{P}}_{{\mathbf{Z}}^i,{\mathbf{Z}}^j}\left[\log \mathcal{P}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)\right]=0}$
一种常用的近似方法是引入variational distribution（变分分布）$\mathcal{Q}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)$,
$$\begin{array}{rl}{\mathbb{E}}_{{\mathcal{P}}_{{\mathbf{Z}}^i,{\mathbf{Z}}^j}}\left[\log \mathcal{P}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)\right]=& {\mathbb{E}}_{{\mathcal{P}}_{{\mathbf{z}}^i,{\mathbf{Z}}^j}}\left[\log \mathcal{Q}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)\right]+\\ & D_{\mathrm{K}\mathrm{L}}\left(\mathcal{P}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)\Vert \mathcal{Q}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)\right)\end{array}$$
这种变分分布$\mathcal{Q}$可以是任何类型，如高斯分布和拉普拉斯分布。实际上，我们简单地假设分布$\mathcal{Q}$为高斯分布$\mathcal{N}\left({\mathbf{Z}}^i\mid G^{(j)}\left({\mathbf{Z}}^j\right),\sigma \mathbf{I}\right)$，其中，$G^{(j)}\left(\cdot \right)$可以是一个将${\mathbf{Z}}^j$映射到${\mathbf{Z}}^i$的参数化模型，$\sigma \mathbf{I}$ 是方差矩阵。通过忽略高斯分布得出的常数，最大化${\mathbb{E}}_{{\mathcal{P}}_{{\mathbf{z}}^i,{\mathbf{Z}}^j}}\left[\log \mathcal{Q}\left({\mathbf{Z}}^i\mid {\mathbf{Z}}^j\right)\right]$相当于
$\min {\mathbb{E}}_{{\mathcal{P}}_{{\mathbf{Z}}^i,{\mathbf{Z}}^j}}{\Vert {\mathbf{Z}}^i-G^{(j)}\left({\mathbf{Z}}^j\right)\Vert }_2^2$
对于给定的双视图数据集，有：
$${\mathcal{L}}_{\text{pre }}={\Vert G^{(1)}\left({\mathbf{Z}}^1\right)-{\mathbf{Z}}^2\Vert }_2^2+{\Vert G^{(2)}\left({\mathbf{Z}}^2\right)-{\mathbf{Z}}^1\Vert }_2^2$$

需要指出的是，上述损失可能导致无视图内重建损失的平凡解，即${\mathbf{Z}}^1$和${\mathbf{Z}}^2$等效相同常数。

模型收敛后，通过双重映射，可以很容易地从${\overline{\mathbf{Z}}}^j$预测缺失的表示${\overline{\mathbf{Z}}}^i$，即：
$${\overline{\mathbf{Z}}}^i=G^{(j)}\left({\overline{\mathbf{Z}}}^j\right)=G^{(j)}\left(f^{(j)}\left({\overline{\mathbf{X}}}^j\right)\right)$$