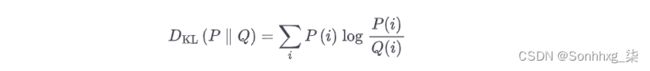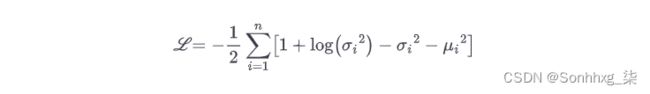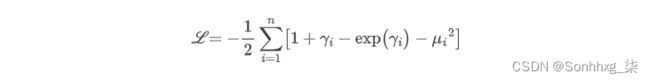【ML】 第17章 使用自动编码器和 GAN 的表示学习和生成学习

 大家好，我是Sonhhxg_柒，希望你看完之后，能对你有所帮助，不足请指正！共同学习交流

个人主页－Sonhhxg_柒的博客_CSDN博客 

欢迎各位→点赞 + 收藏⭐️ + 留言​

系列专栏 - 机器学习【ML】 自然语言处理【NLP】  深度学习【DL】

​

 foreword

✔说明⇢本人讲解主要包括Python、机器学习（ML）、深度学习（DL）、自然语言处理（NLP）等内容。

如果你对这个系列感兴趣的话，可以关注订阅哟

 自动编码器是人工神经网络，能够学习输入数据的密集表示，称为潜在表示或编码，无需任何监督（即，训练集未标记）。这些编码通常具有比输入数据低得多的维度，这使得自动编码器可用于降维（参见第 8 章），尤其是用于可视化目的。自编码器也可以作为特征检测器，它们可以用于深度神经网络的无监督预训练（正如我们在第 11 章中讨论的那样）。最后，一些自编码器是生成模型：它们能够随机生成看起来与训练数据非常相似的新数据。例如，您可以在人脸图片上训练自动编码器，然后它就能够生成新的人脸。然而，生成的图像通常是模糊的，并不完全真实。

在相比之下，生成对抗网络 (GAN) 生成的面孔现在如此令人信服，以至于很难相信它们所代表的人不存在。您可以通过访问This Person Does Not Exist自行判断，该网站显示由最近的 GAN 架构生成的人脸StyleGAN（您也可以查看Spacious House Near City - Guest suites for Rent以查看一些生成的 Airbnb 卧室）。GAN 现在广泛用于超分辨率（提高图像的分辨率）、着色，强大的图像编辑（例如，用逼真的背景替换照片轰炸机），将简单的草图变成逼真的图像，预测视频中的下一帧，扩充数据集（以训练其他模型），生成其他类型的数据（例如文本、音频和时间序列），识别其他模型的弱点并加强它们等等。

自动编码器和 GAN 都是无监督的，它们都学习密集表示，它们都可以用作生成模型，并且它们有许多相似的应用。但是，它们的工作方式非常不同：

• 自动编码器只是学习将输入复制到输出。这听起来可能是一项微不足道的任务，但我们会看到以各种方式约束网络会使它变得相当困难。例如，您可以限制潜在表示的大小，或者您可以向输入添加噪声并训练网络以恢复原始输入。这些约束阻止自动编码器将输入直接复制到输出，这迫使它学习表示数据的有效方法。简而言之，编码是自编码器在某些约束下学习恒等函数的副产品。

• GAN由两个神经网络组成：一个尝试生成与训练数据相似的数据的生成器，以及一个尝试将真实数据与假数据区分开来的鉴别器。这种架构在深度学习中非常新颖，因为生成器和鉴别器在训练期间相互竞争：生成器通常被比作试图制造假币的罪犯，而鉴别器就像试图说出真钱的警察调查员从假的。对抗性训练（训练竞争性神经网络）被广泛认为是近年来最重要的思想之一。2016 年，Yann LeCun 甚至说这是“机器学习过去 10 年中最有趣的想法”。

在本章中，我们将首先更深入地探索自动编码器的工作原理以及如何将它们用于降维、特征提取、无监督预训练或作为生成模型。这自然会将我们引向 GAN。我们将从构建一个简单的 GAN 来生成假图像开始，但我们会发现训练通常非常困难。我们将讨论对抗性训练遇到的主要困难，以及解决这些困难的一些主要技术。让我们从自动编码器开始吧！

高效的数据表示

哪个在下列数字序列中，你觉得最容易记住吗？

• 40, 27, 25, 36, 81, 57, 10, 73, 19, 68

• 50, 48, 46, 44, 42, 40, 38, 36, 34, 32, 30, 28, 26, 24, 22, 20, 18, 16, 14

乍一看，似乎第一个序列应该更容易，因为它要短得多。然而，如果你仔细看第二个序列，你会注意到它只是从 50 到 14 的偶数列表。一旦你注意到这种模式，第二个序列就变得比第一个更容易记住，因为你只需要记住模式（即减少偶数）以及开始和结束数字（即50和14）。请注意，如果您可以快速轻松地记住很长的序列，那么您就不会太在意第二个序列中是否存在模式。您只需背诵每个数字，就是这样。很难记住长序列的事实使得识别模式很有用，

记忆与知觉之间的关系William Chase 和 Herbert Simon 在 1970 年代早期对模式匹配进行了著名的研究。1他们观察到，国际象棋专家只需注视棋盘 5 秒钟，就能记住一盘棋中所有棋子的位置，这是大多数人认为不可能完成的任务。但是，只有将棋子放置在真实位置（来自实际游戏）时才会出现这种情况，而不是随机放置棋子时。国际象棋专家的记忆力并不比你我好多少；由于他们的游戏经验，他们只是更容易看到国际象棋图案。注意到模式有助于他们有效地存储信息。

就像这个记忆实验中的棋手一样，自动编码器查看输入，将它们转换为有效的潜在表示，然后吐出（希望）看起来非常接近输入的东西。自动编码器总是由两部分组成：一个将输入转换为潜在表示的编码器（或识别网络），然后是一个将内部表示转换为输出的解码器（或生成网络）（见图 17-1）。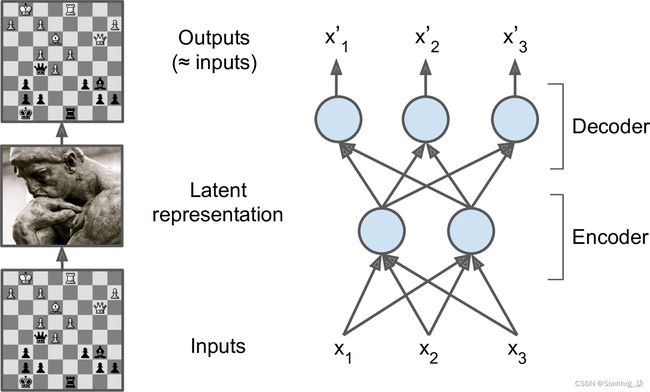

图 17-1。国际象棋记忆实验（左）和一个简单的自动编码器（右）

如您所见，自编码器通常具有与多层感知器（MLP；参见第 10 章）相同的架构，只是输出层中的神经元数量必须等于输入的数量。在这个例子中，只有一个隐藏层由两个神经元组成（编码器），一个输出层由三个神经元组成（解码器）。输出通常是之所以称为重构，是因为自动编码器尝试重构输入，并且成本函数包含重构损失，当重构与输入不同时，该损失会惩罚模型。

因为内部表示的维数比输入数据低（它是 2D 而不是 3D），所以自动编码器据说是不完整的。一个不完整的自动编码器不能轻易地将其输入复制到编码中，但它必须找到一种方法来输出其输入的副本。它被迫学习输入数据中最重要的特征（并丢弃不重要的特征）。

让我们看看如何实现一个非常简单的不完全自编码器来进行降维。

使用不完全线性自动编码器执行 PCA

如果自编码器仅使用线性激活和成本函数是均方误差（MSE），然后它最终执行主成分分析（PCA；参见第 8 章）。

以下代码构建了一个简单的线性自动编码器，以在 3D 数据集上执行 PCA，并将其投影到 2D：

from tensorflow import keras

encoder = keras.models.Sequential([keras.layers.Dense(2, input_shape=[3])])
decoder = keras.models.Sequential([keras.layers.Dense(3, input_shape=[2])])
autoencoder = keras.models.Sequential([encoder, decoder])

autoencoder.compile(loss="mse", optimizer=keras.optimizers.SGD(lr=0.1))

这段代码与我们在过去章节中构建的所有 MLP 并没有太大区别，但有几点需要注意：

• 我们将自动编码器组织成两个子组件：编码器和解码器。两者都是Sequential具有单层的常规模型Dense，而自动编码器是Sequential包含编码器和解码器的模型（请记住，模型可以用作另一个模型中的层）。

• 自动编码器的输出数量等于输入数量（即 3）。

• 为了执行简单的 PCA，我们不使用任何激活函数（即所有神经元都是线性的），成本函数是 MSE。我们很快就会看到更复杂的自动编码器。

现在让我们在一个简单的生成 3D 数据集上训练模型，并使用它来编码相同的数据集（即，将其投影到 2D）：

history = autoencoder.fit(X_train, X_train, epochs=20)
codings = encoder.predict(X_train)

请注意，相同的数据集X_train被用作输入和目标。图 17-2显示了原始 3D 数据集（左侧）和自动编码器隐藏层（即编码层，右侧）的输出。如您所见，自动编码器找到了将数据投影到的最佳 2D 平面，尽可能多地保留数据中的差异（就像 PCA 一样）。

图 17-2。由不完全线性自动编码器执行的 PCA

笔记

您可以将自动编码器视为自监督学习的一种形式（即，使用具有自动生成标签的监督学习技术，在这种情况下，简单地等于输入）。

堆叠式自动编码器（Stacked Autoencoders）

只是像我们讨论过的其他神经网络一样，自动编码器可以有多个隐藏层。在这种情况下，它们被称为堆叠自动编码器（或深度自动编码器）。添加更多层有助于自动编码器学习更复杂的编码。也就是说，必须小心不要让自动编码器过于强大。想象一个如此强大的编码器，它只学习将每个输入映射到一个任意数字（解码器学习反向映射）。显然，这样的自动编码器将完美地重建训练数据，但它不会在此过程中学习任何有用的数据表示（并且不太可能很好地推广到新实例）。

堆叠式自动编码器的架构通常相对于中央隐藏层（编码层）是对称的。简单地说，它看起来像一个三明治。例如，MNIST 的自动编码器（在第 3 章中介绍）可能有 784 个输入，然后是具有 100 个神经元的隐藏层，然后是具有 30 个神经元的中央隐藏层，然后是具有 100 个神经元的另一个隐藏层，以及具有 784 个神经元的输出层神经元。这种堆叠的自动编码器如图 17-3 所示。

图 17-3。堆叠式自动编码器

使用 Keras 实现堆叠式自动编码器

你可以像常规的深度 MLP 一样实现堆叠式自动编码器。特别是，可以应用我们在第 11 章中用于训练深度网络的相同技术。例如，以下代码使用 SELU激活函数为 Fashion MNIST（如第 10 章加载和规范化）构建了一个堆叠自动编码器：

stacked_encoder = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dense(100, activation="selu"),
    keras.layers.Dense(30, activation="selu"),
])
stacked_decoder = keras.models.Sequential([
    keras.layers.Dense(100, activation="selu", input_shape=[30]),
    keras.layers.Dense(28 * 28, activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])
stacked_ae = keras.models.Sequential([stacked_encoder, stacked_decoder])
stacked_ae.compile(loss="binary_crossentropy",
                   optimizer=keras.optimizers.SGD(lr=1.5))
history = stacked_ae.fit(X_train, X_train, epochs=10,
                         validation_data=[X_valid, X_valid])

让我们看一下这段代码：

• 就像之前一样，我们将自动编码器模型拆分为两个子模型：编码器和解码器。

• 编码器获取 28 × 28 像素的灰度图像，将它们展平，以便将每个图像表示为大小为 784 的矢量，然后通过两个Dense尺寸递减的层（100 个单位然后 30 个单位）处理这些矢量，均使用 SELU 激活函数（您可能还想添加 LeCun 正常初始化，但网络不是很深，所以不会有很大的不同）。对于每个输入图像，编码器输出一个大小为 30 的向量。

• 解码器采用大小为 30 的编码（由编码器输出）并通过Dense两层大小递增（100 个单元然后 784 个单元）对其进行处理，并将最终向量重塑为 28 × 28 数组，因此解码器的输出具有与编码器的输入。

• 在编译堆叠自动编码器时，我们使用二元交叉熵损失而不是均方误差。我们将重建任务视为多标签二元分类问题：每个像素强度代表像素应该为黑色的概率。以这种方式构建它（而不是作为回归问题）往往会使模型收敛得更快。2

• X_train最后，我们将模型用作输入和目标（类似地，我们X_valid同时用作验证输入和目标）来训练模型。

可视化重建

一确保自动编码器得到正确训练的方法是比较输入和输出：差异不应该太显着。让我们从验证集中绘制一些图像，以及它们的重建：

def plot_image(image):
    plt.imshow(image, cmap="binary")
    plt.axis("off")

def show_reconstructions(model, n_images=5):
    reconstructions = model.predict(X_valid[:n_images])
    fig = plt.figure(figsize=(n_images * 1.5, 3))
    for image_index in range(n_images):
        plt.subplot(2, n_images, 1 + image_index)
        plot_image(X_valid[image_index])
        plt.subplot(2, n_images, 1 + n_images + image_index)
        plot_image(reconstructions[image_index])

show_reconstructions(stacked_ae)

图 17-4显示了生成的图像。

图 17-4。原始图像（上）及其重建（下）

重建是可识别的，但有点太有损了。我们可能需要更长时间地训练模型，或者使编码器和解码器更深，或者使编码更大。但是，如果我们让网络变得过于强大，它将设法进行完美的重建，而无需在数据中学习任何有用的模式。现在，让我们使用这个模型。

可视化Fashion MNIST数据集

现在我们已经训练了一个堆叠的自动编码器，我们可以使用它来降低数据集的维度。对于可视化，与其他降维算法（例如我们在第 8 章中讨论的那些）相比，这并没有给出很好的结果，但是自动编码器的一大优势是它们可以处理具有许多实例和许多特征的大型数据集。所以一种策略是使用自动编码器将维度降低到合理的水平，然后使用另一种降维可视化算法。让我们使用这个策略来可视化 Fashion MNIST。首先，我们使用堆叠自动编码器中的编码器将维度降低到 30，然后我们使用 Scikit-Learn 的 t-SNE 算法实现将维度降低到 2 以进行可视化：

from sklearn.manifold import TSNE

X_valid_compressed = stacked_encoder.predict(X_valid)
tsne = TSNE()
X_valid_2D = tsne.fit_transform(X_valid_compressed)

现在我们可以绘制数据集：

plt.scatter(X_valid_2D[:, 0], X_valid_2D[:, 1], c=y_valid, s=10, cmap="tab10")

图 17-5显示了生成的散点图（通过显示一些图像进行了美化）。t-SNE 算法识别出几个与类匹配得相当好的集群（每个类用不同的颜色表示）。

图 17-5。使用自动编码器和 t-SNE 进行时尚 MNIST 可视化

因此，自动编码器可用于降维。另一个应用是无监督预训练。

使用堆叠自动编码器的无监督预训练

作为我们在第 11 章中讨论过，如果您正在处理一项复杂的监督任务，但您没有大量标记的训练数据，一个解决方案是找到一个执行类似任务并重用其较低层的神经网络。这使得使用少量训练数据训练高性能模型成为可能，因为您的神经网络不必学习所有低级特征；它只会重用现有网络学习的特征检测器。

同样，如果您有一个大型数据集，但其中大部分没有标记，您可以首先使用所有数据训练一个堆叠的自动编码器，然后重用较低的层为您的实际任务创建一个神经网络，并使用标记的数据对其进行训练。例如，图 17-6展示了如何使用堆叠式自动编码器对分类神经网络执行无监督预训练。在训练分类器时，如果你真的没有太多标记的训练数据，你可能想要冻结预训练的层（至少是较低的层）。

图 17-6。使用自动编码器进行无监督预训练

笔记

拥有大量未标记数据和少量标记数据是很常见的。构建大型未标记数据集通常很便宜（例如，一个简单的脚本可以从互联网上下载数百万张图像），但标记这些图像（例如，将它们分类为可爱与否）通常只能由人类可靠地完成。标记实例既耗时又昂贵，因此只有几千个人工标记的实例是正常的。

实现没有什么特别之处：只需使用所有训练数据（标记和未标记）训练一个自动编码器，然后重用其编码器层来创建一个新的神经网络（参见本章末尾的练习中的示例）。

接下来，让我们看一些用于训练堆叠自编码器的技术。

捆绑重量（Tying Weights）

什么时候自编码器是整齐对称的，就像我们刚刚构建的那样，一种常见的技术是将解码器层的权重与编码器层的权重联系起来。这将模型中的权重数量减半，加快了训练速度并限制了过度拟合的风险。具体来说，如果自编码器总共有N层（不包括输入层），W L表示第L层的连接权重（例如，第1层是第一个隐藏层，第N /2层是编码层，并且第N层是输出层），那么解码器层的权重可以简单地定义为：W (N–L +1 )= WL ⊺（其中 L = 1, 2, ..., N /2）。

要使用 Keras 在层之间绑定权重，让我们定义一个自定义层：

class DenseTranspose(keras.layers.Layer):
    def __init__(self, dense, activation=None, **kwargs):
        self.dense = dense
        self.activation = keras.activations.get(activation)
        super().__init__(**kwargs)
    def build(self, batch_input_shape):
        self.biases = self.add_weight(name="bias", initializer="zeros",
                                      shape=[self.dense.input_shape[-1]])
        super().build(batch_input_shape)
    def call(self, inputs):
        z = tf.matmul(inputs, self.dense.weights[0], transpose_b=True)
        return self.activation(z + self.biases)

这个自定义层的作用类似于常规Dense层，但它使用另一个Dense层的权重，转置（设置transpose_b=True相当于转置第二个参数，但它更有效，因为它在matmul()操作中动态执行转置）。但是，它使用自己的偏置向量。接下来，我们可以构建一个新的堆叠式自动编码器，与前一个非常相似，但解码器的Dense层与编码器的Dense层相关联：

dense_1 = keras.layers.Dense(100, activation="selu")
dense_2 = keras.layers.Dense(30, activation="selu")

tied_encoder = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    dense_1,
    dense_2
])


tied_decoder = keras.models.Sequential([
    DenseTranspose(dense_2, activation="selu"),
    DenseTranspose(dense_1, activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])

tied_ae = keras.models.Sequential([tied_encoder, tied_decoder])

该模型的重建误差比之前的模型要低得多，参数数量几乎只有一半。

一次训练一个自动编码器

相当与像我们刚才那样一次性训练整个堆叠式自动编码器相比，可以一次训练一个浅层自动编码器，然后将它们全部堆叠成一个堆叠式自动编码器（因此得名），如图 17-7所示。这种技术现在使用得不多，但你可能仍然会遇到谈论“贪婪分层训练”的论文，所以很高兴知道它的含义。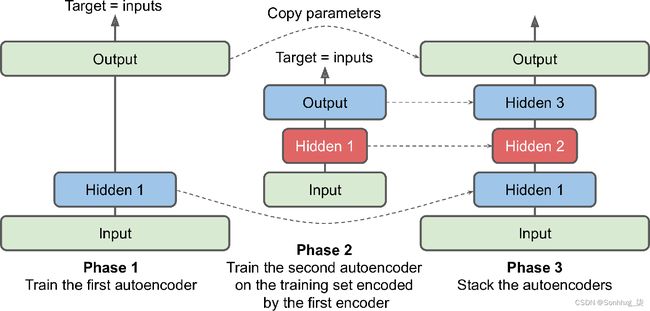

图 17-7。一次训练一个自动编码器

在训练的第一阶段，第一个自动编码器学习重建输入。然后我们使用第一个自动编码器对整个训练集进行编码，这给了我们一个新的（压缩的）训练集。然后，我们在这个新数据集上训练第二个自动编码器。这是训练的第二阶段。最后，我们使用所有这些自动编码器构建了一个大三明治，如图 17-7所示（即，我们首先堆叠每个自动编码器的隐藏层，然后以相反的顺序堆叠输出​​层）。这为我们提供了最终的堆叠式自动编码器（有关实现，请参见笔记本中的“一次训练一个自动编码器”部分）。我们可以通过这种方式轻松地训练更多的自动编码器，构建一个非常深的堆叠自动编码器。

正如我们之前所讨论的，当前对深度学习感兴趣的海啸的触发因素之一是Geoffrey Hinton 等人在 2006 年的发现。可以使用这种贪婪的分层方法以无监督的方式对深度神经网络进行预训练。为此，他们使用受限玻尔兹曼机（RBM；见附录 E ），但在2007 年 Yoshua Bengio 等人。显示3自动编码器也能正常工作。多年来，这是训练深度网络的唯一有效方法，直到第 11 章介绍的许多技术使得一次性训练深度网络成为可能。

自编码器不仅限于密集网络：您还可以构建卷积自编码器，甚至是循环自编码器。现在让我们看看这些。

卷积自动编码器（Convolutional Autoencoders）

如果如果你正在处理图像，那么到目前为止我们看到的自动编码器将无法正常工作（除非图像非常小）：正如我们在第 14 章中看到的，卷积神经网络比密集网络更适合处理图像。因此，如果您想为图像构建一个自动编码器（例如，用于无监督预训练或降维），您将需要构建一个卷积自动编码器。4编码器是由卷积层和池化层组成的常规 CNN。它通常会降低输入的空间维度（即高度和宽度），同时增加深度（即特征图的数量）。解码器必须做相反的事情（放大图像并将其深度降低回原始尺寸），为此您可以使用转置卷积层（或者，您可以将上采样层与卷积层结合起来）。这是 Fashion MNIST 的简单卷积自动编码器：

conv_encoder = keras.models.Sequential([
    keras.layers.Reshape([28, 28, 1], input_shape=[28, 28]),
    keras.layers.Conv2D(16, kernel_size=3, padding="same", activation="selu"),
    keras.layers.MaxPool2D(pool_size=2),
    keras.layers.Conv2D(32, kernel_size=3, padding="same", activation="selu"),
    keras.layers.MaxPool2D(pool_size=2),
    keras.layers.Conv2D(64, kernel_size=3, padding="same", activation="selu"),
    keras.layers.MaxPool2D(pool_size=2)
])
conv_decoder = keras.models.Sequential([
    keras.layers.Conv2DTranspose(32, kernel_size=3, strides=2, padding="valid",
                                 activation="selu",
                                 input_shape=[3, 3, 64]),
    keras.layers.Conv2DTranspose(16, kernel_size=3, strides=2, padding="same",
                                 activation="selu"),
    keras.layers.Conv2DTranspose(1, kernel_size=3, strides=2, padding="same",
                                 activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])
conv_ae = keras.models.Sequential([conv_encoder, conv_decoder])

循环自动编码器（Recurrent Autoencoders）

如果如果你想为序列构建一个自动编码器，比如时间序列或文本（例如，用于无监督学习或降维），那么循环神经网络（参见第 15 章）可能比密集网络更适合。构建循环自动编码器很简单：编码器通常是一个序列到向量的 RNN，它将输入序列压缩为单个向量。解码器是一个向量到序列的 RNN，它执行相反的操作：

recurrent_encoder = keras.models.Sequential([
    keras.layers.LSTM(100, return_sequences=True, input_shape=[None, 28]),
    keras.layers.LSTM(30)
])
recurrent_decoder = keras.models.Sequential([
    keras.layers.RepeatVector(28, input_shape=[30]),
    keras.layers.LSTM(100, return_sequences=True),
    keras.layers.TimeDistributed(keras.layers.Dense(28, activation="sigmoid"))
])
recurrent_ae = keras.models.Sequential([recurrent_encoder, recurrent_decoder])

这种循环自动编码器可以处理任意长度的序列，每个时间步有 28 个维度。方便的是，这意味着它可以通过将每个图像视为一系列行来处理 Fashion MNIST 图像：在每个时间步，RNN 将处理 28 个像素的单行。显然，您可以对任何类型的序列使用循环自动编码器。请注意，我们使用一个RepeatVector层作为解码器的第一层，以确保其输入向量在每个时间步都被馈送到解码器。

好的，让我们退后一步。到目前为止，我们已经看到了各种类型的自动编码器（基本的、堆叠的、卷积的和循环的），并且我们已经研究了如何训练它们（一次性或逐层）。我们还研究了几个应用：数据可视化和无监督预训练。

到目前为止，为了强制自动编码器学习有趣的特征，我们限制了编码层的大小，使其不完整。实际上还有许多其他类型的约束可以使用，包括允许编码层与输入一样大，甚至更大的约束，从而导致在一个过完备的自动编码器中。现在让我们看看其中的一些方法。

去噪自编码器（Denoising Autoencoders）

其他强制自动编码器学习有用特征的方法是在其输入中添加噪声，训练它以恢复原始的无噪声输入。这个想法自 1980 年代就已经存在（例如，它在 Yann LeCun 1987 年的硕士论文中提到）。在2008 年的一篇论文中，5 Pascal Vincent 等人。表明自动编码器也可用于特征提取。在2010 年的一篇论文中，6文森特等。引入了堆叠去噪自编码器。

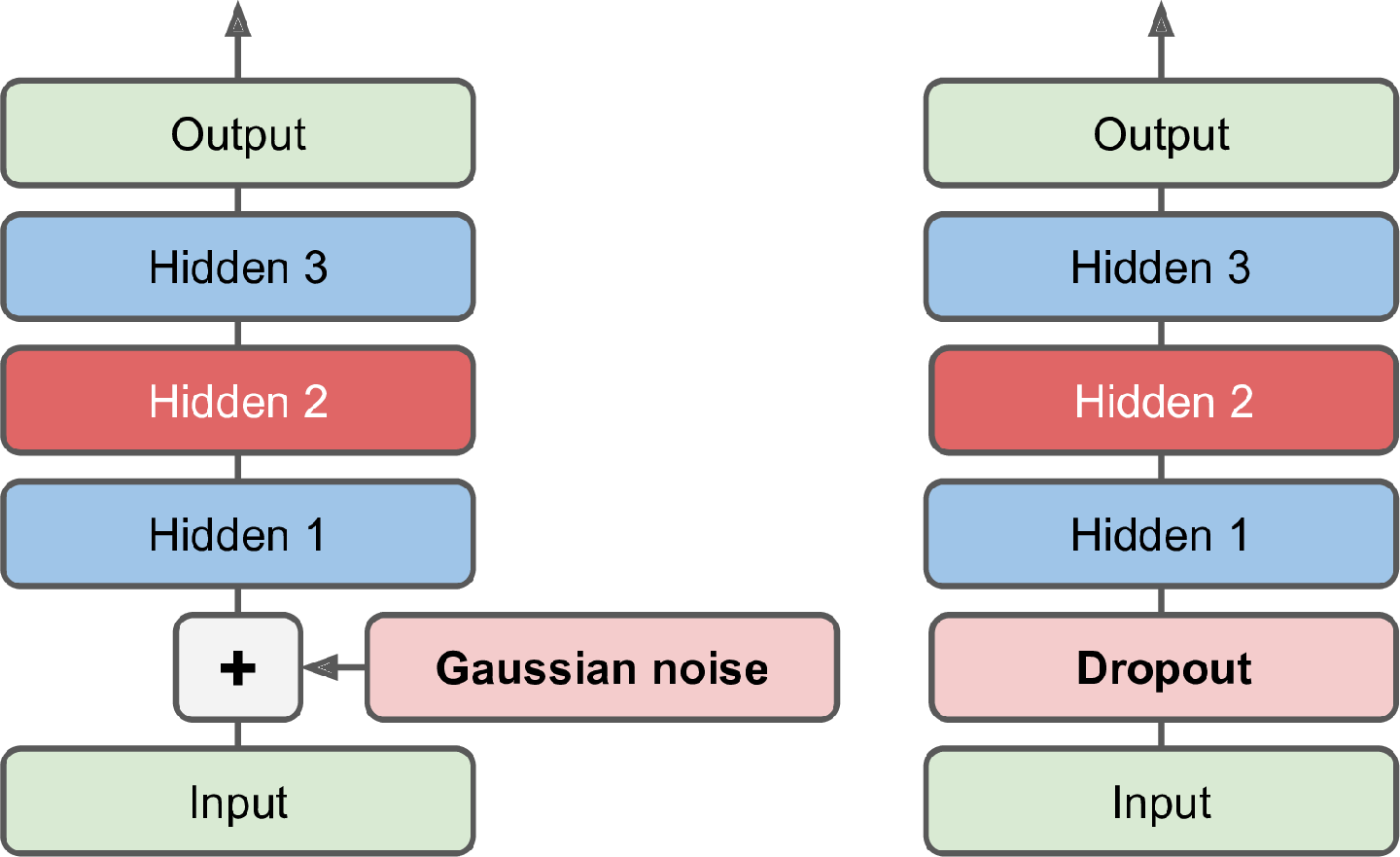
噪声可以是添加到输入的纯高斯噪声，也可以是随机关闭的输入，就像在 dropout 中一样（在第 11 章中介绍）。图 17-8显示了这两个选项。

图 17-8。去噪自编码器，具有高斯噪声（左）或 dropout（右）

实现很简单：它是一个常规的堆叠自动Dropout编码器，在编码器的输入上应用了一个附加层（或者您可以使用一个GaussianNoise层代替）。回想一下，该Dropout层仅在训练期间处于活动状态（该层也是如此GaussianNoise）：

dropout_encoder = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dropout(0.5),
    keras.layers.Dense(100, activation="selu"),
    keras.layers.Dense(30, activation="selu")
])
dropout_decoder = keras.models.Sequential([
    keras.layers.Dense(100, activation="selu", input_shape=[30]),
    keras.layers.Dense(28 * 28, activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])
dropout_ae = keras.models.Sequential([dropout_encoder, dropout_decoder])

图 17-9显示了一些噪声图像（关闭了一半像素），以及由基于 dropout 的去噪自动编码器重建的图像。请注意自动编码器如何猜测实际上不在输入中的细节，例如白衬衫的顶部（底行，第四张图像）。如您所见，去噪自编码器不仅可以用于数据可视化或无监督预训练，就像我们目前讨论的其他自编码器一样，而且它们还可以非常简单有效地用于从图像中去除噪声。

图 17-9。噪声图像（上）及其重建（下）

稀疏自动编码器（Sparse Autoencoders）

另一种通常导致良好特征提取的约束是稀疏性：通过向成本函数添加适当的项，自动编码器被推动以减少编码层中活动神经元的数量。例如，它可能会被迫在编码层中平均只有 5% 的显着活跃神经元。这迫使自动编码器将每个输入表示为少量激活的组合。结果，编码层中的每个神经元通常最终代表一个有用的特征（如果你每个月只能说几个词，你可能会尝试让它们值得一听）。

一种简单的方法是在编码层中使用 sigmoid 激活函数（将编码限制在 0 和 1 之间的值），使用大型编码层（例如，具有 300 个单元），并在编码层的激活（解码器只是一个常规解码器）：

sparse_l1_encoder = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dense(100, activation="selu"),
    keras.layers.Dense(300, activation="sigmoid"),
    keras.layers.ActivityRegularization(l1=1e-3)
])
sparse_l1_decoder = keras.models.Sequential([
    keras.layers.Dense(100, activation="selu", input_shape=[300]),
    keras.layers.Dense(28 * 28, activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])
sparse_l1_ae = keras.models.Sequential([sparse_l1_encoder, sparse_l1_decoder])

该ActivityRegularization层仅返回其输入，但作为副作用，它增加了等于其输入绝对值总和的训练损失（该层仅在训练期间产生影响）。等效地，您可以删除该ActivityRegularization层并activity_regularizer=keras.regularizers.l1(1e-3)在前一层中设置。这种惩罚将鼓励神经网络产生接近 0 的编码，但由于如果它不能正确重构输入也会受到惩罚，因此它必须输出至少一些非零值。使用 ℓ 1范数而不是 ℓ 2范数将推动神经网络保留最重要的编码，同时消除输入图像不需要的编码（而不是仅仅减少所有编码）。

另一种通常产生更好结果的方法是在每次训练迭代时测量编码层的实际稀疏度，并在测量的稀疏度与目标稀疏度不同时惩罚模型。我们通过在整个训练批次中计算编码层中每个神经元的平均激活来做到这一点。批量大小不能太小，否则平均值将不准确。

一次我们有每个神经元的平均激活，我们想通过在成本函数中添加稀疏损失来惩罚过于活跃或不够活跃的神经元。例如，如果我们测量一个神经元的平均激活为 0.3，但目标稀疏度为 0.1，则必须对其进行惩罚以减少激活。一种方法是简单地将平方误差 (0.3 – 0.1) 2添加到成本函数中，但实际上更好的方法是使用具有更强梯度的 Kullback-Leibler (KL) 散度（在第 4 章中简要讨论）比均方误差，如图 17-10 所示。

图 17-10。稀疏损失

给定两个离散概率分布P和Q，这些分布之间的 KL 散度，记为D KL ( P || Q )，可以使用公式 17-1计算。

公式 17-1。Kullback-Leibler 散度

在我们的例子中，我们想要测量编码层中神经元将激活的目标概率p与实际概率q（即训练批次的平均激活）之间的差异。因此 KL 散度简化为公式 17-2。

公式 17-2。目标稀疏度p和实际稀疏度q之间的 KL 散度

一旦我们计算了编码层中每个神经元的稀疏损失，我们将这些损失相加并将结果添加到成本函数中。为了控制稀疏损失和重建损失的相对重要性，我们可以将稀疏损失乘以稀疏权重超参数。如果这个权重太高，模型将紧贴目标稀疏度，但它可能无法正确重建输入，使模型无用。相反，如果它太低，模型将大多忽略稀疏目标，不会学习任何有趣的特征。

我们现在拥有了实现基于 KL 散度的稀疏自动编码器所需的一切。首先，让我们创建一个自定义正则化器来应用 KL 散度正则化：

K = keras.backend
kl_divergence = keras.losses.kullback_leibler_divergence

class KLDivergenceRegularizer(keras.regularizers.Regularizer):
    def __init__(self, weight, target=0.1):
        self.weight = weight
        self.target = target
    def __call__(self, inputs):
        mean_activities = K.mean(inputs, axis=0)
        return self.weight * (
            kl_divergence(self.target, mean_activities) +
            kl_divergence(1. - self.target, 1. - mean_activities))

现在我们可以构建稀疏自动编码器，使用KLDivergenceRegularizer编码层的激活：

kld_reg = KLDivergenceRegularizer(weight=0.05, target=0.1)
sparse_kl_encoder = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dense(100, activation="selu"),
    keras.layers.Dense(300, activation="sigmoid", activity_regularizer=kld_reg)
])
sparse_kl_decoder = keras.models.Sequential([
    keras.layers.Dense(100, activation="selu", input_shape=[300]),
    keras.layers.Dense(28 * 28, activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])
sparse_kl_ae = keras.models.Sequential([sparse_kl_encoder, sparse_kl_decoder])

在 Fashion MNIST 上训练这个稀疏自编码器后，编码层中神经元的激活大多接近于 0（大约 70% 的激活低于 0.1），所有神经元的平均激活在 0.1 左右（大约 90%所有神经元的平均激活值都在 0.1 和 0.2 之间），如图 17-11所示。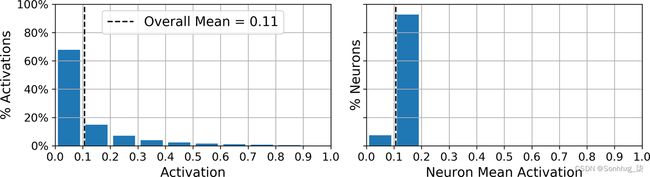

图 17-11。编码层中所有激活的分布（左）和每个神经元的平均激活分布（右）

变分自编码器（Variational Autoencoders）

另一个重要类别自动编码器由 Diederik Kingma 和 Max Welling于 2013 年推出，并迅速成为最流行的自动编码器类型之一：变分自动编码器。7

它们与我们迄今为止讨论的所有自动编码器完全不同，在这些特定方面：

• 他们是概率自动编码器，这意味着它们的输出部分是由偶​​然决定的，即使在训练之后也是如此（与去噪自动编码器相反，它只在训练期间使用随机性）。

• 最多重要的是，它们是生成式自动编码器，这意味着它们可以生成看起来像是从训练集中采样的新实例。

这两个属性都使它们与 RBM 非常相似，但它们更容易训练，并且采样过程要快得多（使用 RBM，您需要等待网络稳定到“热平衡”，然后才能对新实例进行采样） . 事实上，正如他们的名字所暗示的那样，变分自动编码器执行变分贝叶斯推理（在第 9 章中介绍），这是一种执行近似贝叶斯推理的有效方法。

让我们来看看它们是如何工作的。图 17-12（左）显示了一个变分自动编码器。您可以识别所有自动编码器的基本结构，编码器后跟一个解码器（在这个例子中，它们都有两个隐藏层），但是有一个转折：不是直接为给定输入生成编码，而是编码器产生平均编码 μ和标准偏差σ。然后，实际编码是从具有均值μ和标准偏差σ的高斯分布中随机采样的。之后，解码器正常解码采样编码。该图的右侧部分显示了一个通过此自动编码器的训练实例。首先，编码器产生μ和σ，然后随机采样一个编码（注意它并不完全位于μ），最后对这个编码进行解码；最终输出类似于训练实例。

图 17-12。变分自动编码器（左）和经过它的实例（右）

正如您在图中看到的那样，尽管输入可能具有非常复杂的分布，但变分自动编码器倾向于产生看起来好像是从简单的高斯分布中采样的编码：8在训练期间，成本函数（接下来讨论）推动编码在编码空间（也称为潜在空间）内逐渐迁移，最终看起来像一团高斯点。一个重要的结果是，在训练变分自动编码器之后，您可以非常轻松地生成一个新实例：只需从高斯分布中采样一个随机编码，对其进行解码，然后瞧！

现在，让我们看一下成本函数。它由两部分组成。第一个是通常的重建损失，它推动自动编码器重现其输入（我们可以为此使用交叉熵，如前所述）。第二个是推动自动编码器的编码看起来好像是从简单的高斯分布中采样的潜在损失：它是目标分布（即高斯分布）和编码的实际分布之间的 KL 散度。数学比稀疏自动编码器复杂一点，特别是因为高斯噪声，它限制了可以传输到编码层的信息量（从而推动自动编码器学习有用的特征）。幸运的是，方程简化了，因此可以使用方程 17-3非常简单地计算潜在损失：9

公式 17-3。变分自编码器的潜在损失

 在这个等式中，ℒ 是潜在损失，n是编码的维度，μ i和σ i是编码的第i个分量的均值和标准差。向量μ和σ（包含所有μ i和σ i）由编码器输出，如图 17-12（左）所示。

对变分自动编码器架构的一个常见调整是使编码器输出γ = log( σ 2 ) 而不是σ。然后可以如公式 17-4所示计算潜在损失。这种方法在数值上更加稳定并加快了训练速度。

公式 17-4。变分自动编码器的潜在损失，使用γ = log( σ ²)重写

 让我们开始为 Fashion MNIST 构建一个变分自动编码器（如图 17-12所示，但使用了γ调整）。首先，我们需要一个自定义层来对编码进行采样，给定μ和γ：

class Sampling(keras.layers.Layer):
    def call(self, inputs):
        mean, log_var = inputs
        return K.random_normal(tf.shape(log_var)) * K.exp(log_var / 2) + mean

该Sampling层有两个输入：mean（μ）和log_var（γ）。它使用该函数从正态分布中采样一个随机向量（与γK.random_normal()具有相同的形状），平均值为 0，标准差为 1。然后将其乘以 exp( γ  / 2) （等于σ，因为你可以验证），最后加上μ并返回结果。这会从具有平均值μ和标准偏差σ的正态分布中采样编码向量。

接下来，我们可以使用功能 API 创建编码器，因为模型不是完全顺序的：

codings_size = 10

inputs = keras.layers.Input(shape=[28, 28])
z = keras.layers.Flatten()(inputs)
z = keras.layers.Dense(150, activation="selu")(z)
z = keras.layers.Dense(100, activation="selu")(z)
codings_mean = keras.layers.Dense(codings_size)(z)  # μ
codings_log_var = keras.layers.Dense(codings_size)(z)  # γ
codings = Sampling()([codings_mean, codings_log_var])
variational_encoder = keras.Model(
    inputs=[inputs], outputs=[codings_mean, codings_log_var, codings])

请注意，Dense输出codings_mean( μ ) 和codings_log_var( γ ) 的层具有相同的输入（即第二Dense层的输出）。然后我们将两者都传递codings_mean给codings_log_var层Sampling。最后，该variational_encoder模型具有三个输出，以防您要检查 和 的codings_mean值codings_log_var。我们将使用的唯一输出是最后一个 ( codings)。现在让我们构建解码器：

decoder_inputs = keras.layers.Input(shape=[codings_size])
x = keras.layers.Dense(100, activation="selu")(decoder_inputs)
x = keras.layers.Dense(150, activation="selu")(x)
x = keras.layers.Dense(28 * 28, activation="sigmoid")(x)
outputs = keras.layers.Reshape([28, 28])(x)
variational_decoder = keras.Model(inputs=[decoder_inputs], outputs=[outputs])

对于这个解码器，我们可以使用 Sequential API 而不是 Functional API，因为它实际上只是一个简单的层堆栈，与我们迄今为止构建的许多解码器几乎相同。最后，让我们构建变分自编码器模型：

_, _, codings = variational_encoder(inputs)
reconstructions = variational_decoder(codings)
variational_ae = keras.Model(inputs=[inputs], outputs=[reconstructions])

请注意，我们忽略了编码器的前两个输出（我们只想将编码馈送到解码器）。最后，我们必须添加潜在损失和重建损失：

latent_loss = -0.5 * K.sum(
    1 + codings_log_var - K.exp(codings_log_var) - K.square(codings_mean),
    axis=-1)
variational_ae.add_loss(K.mean(latent_loss) / 784.)
variational_ae.compile(loss="binary_crossentropy", optimizer="rmsprop")

我们首先应用公式 17-4来计算批次中每个实例的潜在损失（我们在最后一个轴上求和）。然后我们计算批次中所有实例的平均损失，并将结果除以 784 以确保它与重建损失相比具有适当的规模。事实上，变分自编码器的重建损失应该是像素重建误差的总和，但是当 Keras 计算"binary_crossentropy"损失，它计算所有 784 个像素的平均值，而不是总和。因此，重建损失比我们需要的小 784 倍。我们可以定义一个自定义损失来计算总和而不是平均值，但是将潜在损失除以 784 更简单（最终损失将比应有的小 784 倍，但这只是意味着我们应该使用更大的学习率）。

请注意，我们使用了RMSprop优化器，在这种情况下效果很好。最后我们可以训练自动编码器了！

history = variational_ae.fit(X_train, X_train, epochs=50, batch_size=128,
                             validation_data=[X_valid, X_valid])

生成时尚 MNIST 图像

现在让我们使用这个变分自动编码器来生成看起来像时尚单品的图像。我们需要做的就是从高斯分布中采样随机编码并对其进行解码：

codings = tf.random.normal(shape=[12, codings_size])
images = variational_decoder(codings).numpy()

图 17-13显示了 12 个生成的图像。

图 17-13。变分自动编码器生成的时尚 MNIST 图像

这些图像中的大多数看起来都相当有说服力，如果有点太模糊的话。其余的都不是很好，但不要对自动编码器太苛刻——它只有几分钟的时间来学习！给它更多的微调和训练时间，这些图像应该看起来更好。

变分自动编码器使执行语义插值成为可能：我们可以在编码级别进行插值，而不是在像素级别插值两个图像（看起来好像两个图像重叠）。我们首先通过编码器运行两个图像，然后对得到的两个编码进行插值，最后对插值后的编码进行解码，得到最终图像。它看起来像普通的 Fashion MNIST 图像，但它是原始图像之间的中间图像。在下面的代码示例中，我们取刚刚生成的 12 个编码，将它们组织成一个 3 × 4 的网格，并使用 TensorFlow 的tf.image.resize()函数将这个网格的大小调整为 5 × 7。默认情况下，resize()函数将执行双线性插值，因此每隔一行和一列将包含插值编码。然后我们使用解码器生成所有图像：

codings_grid = tf.reshape(codings, [1, 3, 4, codings_size])
larger_grid = tf.image.resize(codings_grid, size=[5, 7])
interpolated_codings = tf.reshape(larger_grid, [-1, codings_size])
images = variational_decoder(interpolated_codings).numpy()

图 17-14显示了生成的图像。原始图像被框起来，其余的是附近图像之间语义插值的结果。例如，请注意，第四行和第五列中的鞋子是位于其上方和下方的两只鞋子之间的一个很好的插值。

图 17-14。语义插值

几年来，变分自编码器非常流行，但 GAN 最终占据了领先地位，特别是因为它们能够生成更逼真、更清晰的图像。因此，让我们将注意力转向 GAN。

生成对抗网络（Generative Adversarial Networks）

生成对抗网络由 Ian Goodfellow 等人在2014 年的一篇论文10中提出，尽管这个想法几乎立刻让研究人员兴奋不已，但还是花了几年时间才克服了训练 GAN 的一些困难。像许多伟大的想法一样，事后看来，这似乎很简单：让神经网络相互竞争，希望这场竞争能够推动它们脱颖而出。如图 17-15所示，一个 GAN 由两个神经网络组成：

发电机

将随机分布作为输入（通常是高斯分布）并输出一些数据——通常是图像。您可以将随机输入视为要生成的图像的潜在表示（即编码）。所以，正如你所看到的，生成器提供了与变分自动编码器中的解码器相同的功能，并且可以以相同的方式使用它来生成新图像（只需给它一些高斯噪声，它就会输出一个全新的图像）。然而，我们很快就会看到，它的训练方式非常不同。

鉴别器

将生成器中的假图像或训练集中的真实图像作为输入，并且必须猜测输入图像是假的还是真实的。

图 17-15。生成对抗网络

在训练过程中，生成器和判别器有相反的目标：判别器试图将假图像与真实图像区分开来，而生成器试图生成看起来足够真实的图像来欺骗判别器。因为 GAN 由两个具有不同目标的网络组成，所以不能像常规神经网络那样进行训练。每次训练迭代分为两个阶段：

• 在第一阶段，我们训练判别器。从训练集中抽取一批真实图像，并用生成器生成的相同数量的假图像完成。假图像的标签设置为 0，真实图像的标签设置为 1，鉴别器在这个标记的批次上训练一步，使用二元交叉熵损失。重要的是，反向传播仅在此阶段优化鉴别器的权重。

• 在第二阶段，我们训练生成器。我们首先用它来产生另一批假图像，再一次用鉴别器来判断图像是假的还是真的。这次我们不在批次中添加真实图像，所有标签都设置为 1（真实）：换句话说，我们希望生成器生成判别器（错误地）认为是真实的图像！至关重要的是，鉴别器的权重在此步骤中被冻结，因此反向传播仅影响生成器的权重。

笔记

生成器从未真正看到任何真实图像，但它逐渐学会产生令人信服的假图像！它得到的只是通过鉴别器流回的梯度。幸运的是，判别器越好，这些二手梯度中包含的真实图像信息就越多，因此生成器可以取得显着进步。

让我们继续为 Fashion MNIST 构建一个简单的 GAN。

首先，我们需要构建生成器和判别器。生成器类似于自动编码器的解码器，判别器是常规的二元分类器（它以图像为输入，以Dense包含单个单元并使用 sigmoid 激活函数的层结束）。对于每个训练迭代的第二阶段，我们还需要包含生成器和鉴别器的完整 GAN 模型：

codings_size = 30

generator = keras.models.Sequential([
    keras.layers.Dense(100, activation="selu", input_shape=[codings_size]),
    keras.layers.Dense(150, activation="selu"),
    keras.layers.Dense(28 * 28, activation="sigmoid"),
    keras.layers.Reshape([28, 28])
])
discriminator = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dense(150, activation="selu"),
    keras.layers.Dense(100, activation="selu"),
    keras.layers.Dense(1, activation="sigmoid")
])
gan = keras.models.Sequential([generator, discriminator])

接下来，我们需要编译这些模型。由于鉴别器是二元分类器，我们自然可以使用二元交叉熵损失。生成器只会通过gan模型进行训练，所以我们根本不需要编译它。该gan模型也是一个二元分类器，因此可以使用二元交叉熵损失。重要的是，判别器不应在第二阶段进行训练，因此我们在编译gan模型之前使其不可训练：

discriminator.compile(loss="binary_crossentropy", optimizer="rmsprop")
discriminator.trainable = False
gan.compile(loss="binary_crossentropy", optimizer="rmsprop")

笔记

Keras 仅在编译模型时才trainable考虑该属性，因此在运行此代码后，如果我们调用它的方法或它的方法（我们将使用）它是可训练的，而当我们调用这些方法时它是不可训练的模型。discriminator fit()train_on_batch()gan

由于训练循环不寻常，我们不能使用常规fit()方法。相反，我们将编写一个自定义训练循环。为此，我们首先需要创建一个Dataset来遍历图像：

batch_size = 32
dataset = tf.data.Dataset.from_tensor_slices(X_train).shuffle(1000)
dataset = dataset.batch(batch_size, drop_remainder=True).prefetch(1)

我们现在准备好编写训练循环了。让我们将它包装在一个train_gan()函数中：

def train_gan(gan, dataset, batch_size, codings_size, n_epochs=50):
    generator, discriminator = gan.layers
    for epoch in range(n_epochs):
        for X_batch in dataset:
            # phase 1 - training the discriminator
            noise = tf.random.normal(shape=[batch_size, codings_size])
            generated_images = generator(noise)
            X_fake_and_real = tf.concat([generated_images, X_batch], axis=0)
            y1 = tf.constant([[0.]] * batch_size + [[1.]] * batch_size)
            discriminator.trainable = True
            discriminator.train_on_batch(X_fake_and_real, y1)
            # phase 2 - training the generator
            noise = tf.random.normal(shape=[batch_size, codings_size])
            y2 = tf.constant([[1.]] * batch_size)
            discriminator.trainable = False
            gan.train_on_batch(noise, y2)

train_gan(gan, dataset, batch_size, codings_size)

如前所述，您可以在每次迭代中看到两个阶段：

• 在第一阶段，我们将高斯噪声输入生成器以生成假图像，然后我们通过连接相同数量的真实图像来完成这批图像。对于假图像，目标y1设置为 0，对于真实图像，目标设置为 1。然后我们在这批上训练鉴别器。请注意，我们将鉴别器的trainable属性设置为True: 这只是为了消除 Keras 在注意到trainable现在False但True在编译模型时显示的警告（反之亦然）。

• 在第二阶段，我们为 GAN 提供了一些高斯噪声。它的生成器将首先生成假图像，然后鉴别器将尝试猜测这些图像是假的还是真的。我们希望鉴别器相信假图像是真实的，因此目标y2设置为 1。请注意，我们将trainable属性设置为False，再次避免警告。

而已！如果显示生成的图像（见图 17-16），您会看到在第一个 epoch 结束时，它们已经开始看起来像（非常嘈杂的）时尚 MNIST 图像。

不幸的是，图像从来没有真正变得比这更好，你甚至可能会发现 GAN 似乎忘记了它学到的东西的时期。这是为什么？好吧，事实证明，训练 GAN 可能具有挑战性。让我们看看为什么。

图 17-16。GAN 在一个 epoch 训练后生成的图像

训练 GAN 的难点

期间在训练中，生成器和判别器在零和游戏中不断地试图超越对方。随着训练的推进，博弈可能会最终进入博弈论者称之为纳什均衡的状态，以数学家约翰纳什命名：在这种情况下，假设其他玩家不改变他们的策略，没有玩家会更好地改变自己的策略。例如，当每个人都在道路左侧行驶时，就达到了纳什均衡：没有司机最好是唯一一个换边的人。当然，还有第二种可能的纳什均衡：当每个人都靠右行驶时路边。不同的初始状态和动力学可能导致一种平衡或另一种平衡。在此示例中，一旦达到均衡（即与其他人在同一侧行驶），就会有一个最优策略，但纳什均衡可能涉及多种竞争策略（例如，捕食者追逐它的猎物，猎物试图逃跑，改变他们的策略也不会更好）。

那么这如何适用于 GAN 呢？好吧，该论文的作者证明了 GAN 只能达到一个纳什均衡：那就是生成器生成完美逼真的图像，而判别器被迫猜测（50% 真实，50% 虚假）。这个事实非常令人鼓舞：看起来你只需要训练 GAN 足够长的时间，它最终会达到这个平衡，给你一个完美的生成器。不幸的是，事情并没有那么简单：没有什么能保证永远达到平衡。

这最大的困难叫做模式崩溃：这是生成器的输出逐渐变得不那么多样化的时候。这怎么可能发生？假设生成器在生产令人信服的鞋子方面比任何其他类别都做得更好。它会用鞋子更多地欺骗鉴别器，这将鼓励它产生更多的鞋子图像。渐渐地，它会忘记如何生产其他东西。同时，判别器唯一能看到的假图像是鞋子，所以它也会忘记如何辨别其他类别的假图像。最终，当鉴别器设法区分假鞋和真鞋时，生成器将被迫转移到另一个类别。然后它可能会变得擅长衬衫，忘记鞋子，鉴别器会随之而来。GAN 可能会逐渐在几个类别中循环，但从未真正变得非常擅长其中任何一个类别。

此外，由于生成器和判别器不断相互推动，它们的参数最终可能会振荡并变得不稳定。由于这些不稳定性，训练可能会正常开始，然后突然无缘无故地发散。而且由于许多因素会影响这些复杂的动态，因此 GAN 对超参数非常敏感：您可能需要花费大量精力来微调它们。

自 2014 年以来，这些问题一直让研究人员非常忙碌：许多论文都围绕这个主题发表，其中一些提出了新的成本函数11（尽管谷歌研究人员2018 年的一篇论文12质疑其效率）或稳定训练或避免模式崩溃问题的技术。例如，一种流行的技术所谓的经验重放包括将生成器在每次迭代中生成的图像存储在重放缓冲区中（逐渐丢弃较旧的生成图像）并使用真实图像和从该缓冲区中提取的假图像训练鉴别器（而不仅仅是当前生成的假图像）发电机）。这减少了鉴别器过度拟合最新生成器输出的机会。另一种常用技术被称为小批量鉴别：它测量整个批次中图像的相似程度，并将此统计信息提供给鉴别器，因此它可以轻松拒绝整批缺乏多样性的假图像。这鼓励生成器产生更多种类的图像，减少模式崩溃的机会。其他论文只是提出了恰好表现良好的特定架构。

总之，这仍然是一个非常活跃的研究领域，GAN 的动力学仍然没有被完全理解。但好消息是，已经取得了很大的进展，其中一些结果确实令人震惊！因此，让我们看看一些最成功的架构，从几年前最先进的深度卷积 GAN 开始。然后我们将看看两个最近（也更复杂）的架构。

深度卷积 GAN

这2014 年的原始 GAN 论文尝试了卷积层，但只尝试生成小图像。不久之后，许多研究人员尝试基于更深的卷积网络构建 GAN，以获取更大的图像。事实证明这很棘手，因为训练非常不稳定，但 Alec Radford 等人。在尝试了许多不同的架构和超参数之后，终于在 2015 年底取得了成功。他们将他们的架构称为深度卷积 GAN（DCGAN）。13以下是他们为构建稳定的卷积 GAN 提出的主要指导方针：

• 用跨步卷积（在鉴别器中）和转置卷积（在生成器中）替换任何池化层。

• 在生成器和判别器中都使用 Batch Normalization，但在生成器的输出层和判别器的输入层除外。

• 移除完全连接的隐藏层以获得更深的架构。

• 在生成器中对除输出层外的所有层使用 ReLU 激活，输出层应使用 tanh。

• 在所有层的鉴别器中使用leaky ReLU 激活。

这些指南在许多情况下都有效，但并非总是如此，因此您可能仍需要尝试不同的超参数（事实上，只需更改随机种子并再次训练相同的模型有时会奏效）。例如，这是一个与 Fashion MNIST 配合得很好的小型 DCGAN：

codings_size = 100

generator = keras.models.Sequential([
    keras.layers.Dense(7 * 7 * 128, input_shape=[codings_size]),
    keras.layers.Reshape([7, 7, 128]),
    keras.layers.BatchNormalization(),
    keras.layers.Conv2DTranspose(64, kernel_size=5, strides=2, padding="same",
                                 activation="selu"),
    keras.layers.BatchNormalization(),
    keras.layers.Conv2DTranspose(1, kernel_size=5, strides=2, padding="same",
                                 activation="tanh")
])
discriminator = keras.models.Sequential([
    keras.layers.Conv2D(64, kernel_size=5, strides=2, padding="same",
                        activation=keras.layers.LeakyReLU(0.2),
                        input_shape=[28, 28, 1]),
    keras.layers.Dropout(0.4),
    keras.layers.Conv2D(128, kernel_size=5, strides=2, padding="same",
                        activation=keras.layers.LeakyReLU(0.2)),
    keras.layers.Dropout(0.4),
    keras.layers.Flatten(),
    keras.layers.Dense(1, activation="sigmoid")
])
gan = keras.models.Sequential([generator, discriminator])

生成器采用大小为 100 的编码，并将它们投影到 6272 维（7 * 7 * 128），并对结果进行整形以获得 7 × 7 × 128 张量。该张量被批量归一化并馈送到步长为 2 的转置卷积层，该层将其从 7×7 上采样到 14×14，并将其深度从 128 减少到 64。结果再次批量归一化并馈送到另一个转置卷积层步幅为 2 的层，将其从 14 × 14 上采样到 28 × 28，并将深度从 64 减少到 1。该层使用 tanh 激活函数，因此输出范围为 –1 到 1。因此，在训练 GAN 之前，我们需要将训练集重新缩放到相同的范围。我们还需要对其进行重塑以添加通道维度：

X_train = X_train.reshape(-1, 28, 28, 1) * 2. - 1. # reshape and rescale

鉴别器看起来很像用于二进制分类的常规 CNN，除了我们使用跨步卷积（strides=2）而不是使用最大池化层来下采样图像。另请注意，我们使用了leaky ReLU 激活函数。

总的来说，我们尊重 DCGAN 指南，除了我们用BatchNormalization层替换了鉴别器中的Dropout层（否则在这种情况下训练是不稳定的），并且我们用生成器中的 SELU 替换了 ReLU。随意调整这个架构：你会看到它对超参数有多么敏感（尤其是两个网络的相对学习率）。

最后，为了构建数据集，然后编译和训练这个模型，我们使用与之前完全相同的代码。经过 50 个 epoch 的训练后，生成器生成的图像如图 17-17所示。它仍然不完美，但其中许多图像非常令人信服。

图 17-17。DCGAN 在 50 次训练后生成的图像

如果你扩大这个架构并在一个大的人脸数据集上训练它，你可以获得相当逼真的图像。事实上，DCGAN 可以学习非常有意义的潜在表示，如图 17-18 所示：生成了很多图像，其中九张是手动挑选的（左上），其中三个代表戴眼镜的男性，三个代表不戴眼镜的男性，三个代表不戴眼镜的女性。对于这些类别中的每一个，对用于生成图像的编码进行平均，并根据生成的平均编码生成图像（左下）。简而言之，左下角的三个图像中的每一个都代表位于其上方的三个图像的平均值。但这不是在像素级别计算的简单平均值（这将导致三个重叠的人脸），它是在潜在空间中计算的平均值，因此图像看起来仍然像正常人脸。令人惊讶的是，如果你计算戴眼镜的男人，减去不戴眼镜的男人，加上不戴眼镜的女性——每个术语对应一个平均编码——然后你生成与这个编码相对应的图像，你会得到右侧 3 × 3 人脸网格中心的图像：戴眼镜的女人！它周围的其他八张图像是基于相同的向量加上一点噪声生成的，以说明 DCGAN 的语义插值能力。能够在脸上做算术感觉就像科幻小说！

图 17-18。视觉概念的向量算术（DCGAN 论文中图 7 的一部分）14

小费

如果您将每个图像的类别作为额外输入添加到生成器和判别器，它们都将了解每个类别的外观，因此您将能够控制生成器生成的每个图像的类别。这称为条件 GAN 15 (CGAN)。

不过，DCGAN 并不完美。例如，当您尝试使用 DCGAN 生成非常大的图像时，您通常会得到局部令人信服的特征，但总体上不一致（例如，一个袖子比另一个袖子长得多的衬衫）。你怎么能解决这个问题？

GAN 的逐步发展

一个Nvidia 研究人员 Tero Karras 等人在2018 年的一篇论文16中提出了一项重要技术：他们建议在训练开始时生成小图像，然后在生成器和判别器中逐渐添加卷积层以生成越来越大的图像（4 × 4、8 × 8、16 × 16、……、512 × 512、1,024 × 1,024）。这种方法类似于堆叠自动编码器的贪婪逐层训练。额外的层被添加到生成器的末尾和判别器的开头，之前训练的层仍然是可训练的。

例如，当将生成器的输出从 4 × 4 增加到 8 × 8（见图 17-19）时，在现有卷积层（“Conv 1”）中添加一个上采样层（使用最近邻滤波）以产生 8 × 8 个特征图。这些被输入到新的卷积层（“Conv 2”），然后输入到新的输出卷积层。为了避免破坏“Conv 1”的训练权重，我们逐渐淡入两个新的卷积层（在图 17-19中用虚线表示）并淡出原始输出层。为此，最终输出是新输出（权重为α）和原始输出（权重为 1 -  α ）的加权和， α缓慢增加从 0 到 1。当一个新的卷积层被添加到鉴别器时使用类似的淡入/淡出技术（随后是用于下采样的平均池化层）。请注意，所有卷积层都使用"same"填充和步幅为 1，因此它们保留了输入的高度和宽度。这包括原始卷积层，因此它现在产生 8 × 8 输出（因为它的输入现在是 8 × 8）。最后，输出层使用内核大小 1。它们只是将输入投影到所需的颜色通道数（通常为 3）。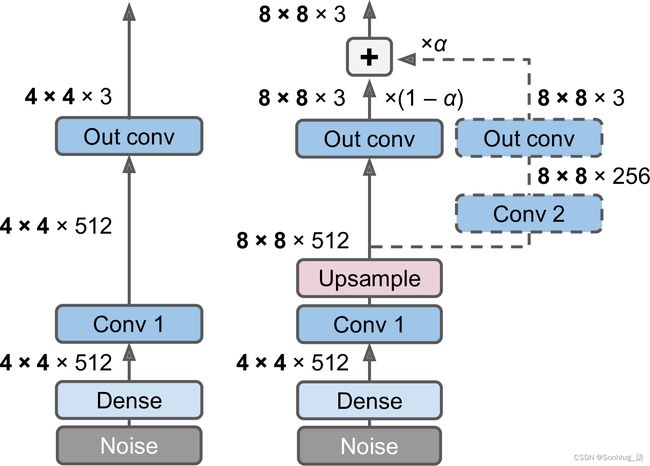

图 17-19。渐进式 GAN：GAN 生成器输出 4 × 4 彩色图像（左）；我们将其扩展为输出 8 × 8 图像（右）

该论文还介绍了其他几种旨在增加输出多样性（以避免模式崩溃）并使训练更加稳定的技术：

Minibatch 标准差层

添加在附近判别器的结束。对于输入中的每个位置，它计算批次中所有通道和所有实例的标准偏差 ( S = tf.math.reduce_std(inputs, axis=[0, -1]))。然后将这些标准偏差在所有点上平均得到一个值 ( v = tf.reduce_​mean(S))。最后，将一个额外的特征图添加到批处理中的每个实例并填充计算值 ( tf.concat([inputs, tf.fill([batch_size, height, width, 1], v)], axis=-1))。这有什么帮助？好吧，如果生成器生成的图像变化不大，那么鉴别器中的特征图之间会有一个小的标准偏差。多亏了这一层，鉴别器将可以轻松访问此统计信息，从而不太可能被产生太少多样性的生成器所愚弄。这将鼓励生成器产生更多样化的输出，从而降低模式崩溃的风险。

均衡学习率

初始化所有权重均使用均值为 0，标准差为 1 的简单高斯分布，而不是使用 He 初始化。然而，权重在运行时（即每次执行层时）按与 He 初始化中相同的因子按比例缩小：它们除以2ninputs，其中n 个输入是该层的输入数。该论文证明，当使用 RMSProp、Adam 或其他自适应梯度优化器时，该技术显着提高了 GAN 的性能。实际上，这些优化器通过估计的标准差（参见第 11 章）对梯度更新进行归一化，因此具有更大动态范围的参数17将需要更长的时间来训练，而动态范围较小的参数可能会更新得太快，导致不稳定。通过重新调整权重作为模型本身的一部分，而不是仅仅在初始化时重新调整它们，这种方法确保了所有参数的动态范围在整个训练过程中都是相同的，因此它们都以相同的速度学习。这既可以加快训练速度又可以稳定训练。

逐像素归一化层

添加在生成器中的每个卷积层之后。它基于相同图像和相同位置但跨所有通道的所有激活对每个激活进行归一化（除以均方激活的平方根）。在 TensorFlow 代码中，这是inputs / tf.sqrt(tf.reduce_mean(tf.square(X), axis=-1, keepdims=True) + 1e-8)（需要平滑项1e-8以避免被零除）。这种技术避免了由于生成器和判别器之间的过度竞争而导致的激活爆炸。

所有这些技术的结合使作者能够生成极具说服力的高清面部图像。但究竟什么是我们所说的“令人信服”？评估是使用 GAN 时的一大挑战：虽然可以自动评估生成图像的多样性，但判断它们的质量是一项更加棘手和主观的任务。一种技术是使用人工评估者，但这是昂贵且耗时的。因此，作者提出考虑每个尺度，测量生成图像的局部图像结构与训练图像之间的相似性。这个想法使他们进行了另一项突破性的创新：StyleGANs。

StyleGAN

国家同一 Nvidia 团队在2018 年的一篇论文18中再次推进了高分辨率图像生成的艺术，该论文介绍了流行的 StyleGAN 架构。作者在生成器中使用了风格迁移技术，以确保生成的图像在每个尺度上都具有与训练图像相同的局部结构，从而大大提高了生成图像的质量。鉴别器和损失函数没有被修改，只有生成器。让我们看一下 StyleGAN。它由两个网络组成（见图 17-20）：

测绘网络

将潜在表示z（即编码）映射到向量w的八层 MLP 。然后发送该向量通过多次仿射变换（即Dense没有激活函数的层，由图 17-20中的“A”框表示），产生多个向量。这些向量在不同级别控制生成图像的风格，从细粒度纹理（例如，头发颜色）到高级特征（例如，成人或儿童）。简而言之，映射网络将编码映射到多个样式向量。

综合网络

负责生成图片。它有一个恒定的学习输入（需要明确的是，这个输入在训练后将是恒定的，但在训练期间它会不断通过反向传播进行调整）。如前所述，它通过多个卷积和上采样层处理此输入，但有两个转折：首先，一些噪声被添加到输入和卷积层的所有输出（在激活函数之前）。二、每个噪声层后面是自适应实例归一化（AdaIN）层：它独立地标准化每个特征图（通过减去特征图的均值并除以其标准差），然后它使用样式向量来确定每个特征图的比例和偏移量（风格向量包含每个特征图的一个尺度和一个偏置项）。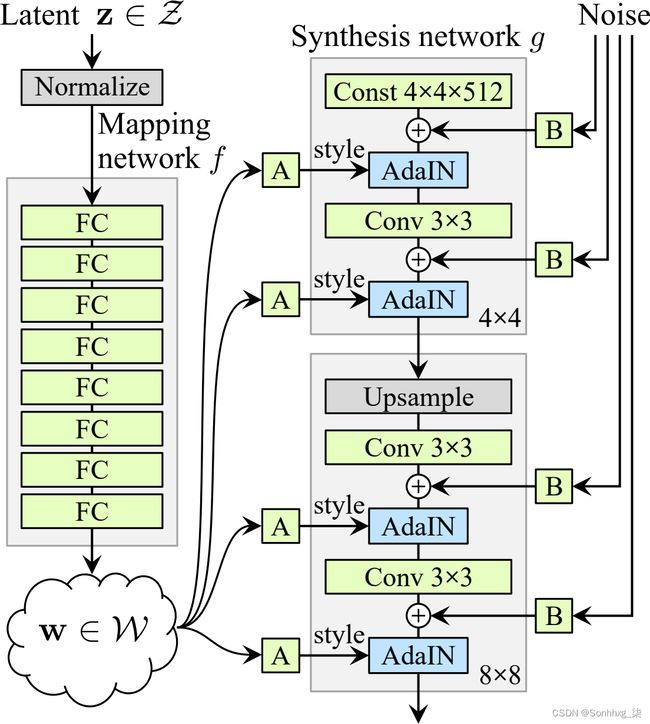

图 17-20。StyleGAN 的生成器架构（来自 StyleGAN 论文的图 1 的一部分）19

独立于编码添加噪声的想法非常重要。图像的某些部分非常随机，例如每个雀斑或头发的确切位置。在早期的 GAN 中，这种随机性要么来自编码，要么是生成器本身产生的一些伪随机噪声。如果它来自编码，则意味着生成器必须将很大一部分编码的表征能力用于存储噪声：这是相当浪费的。此外，噪声必须能够流过网络并到达生成器的最后一层：这似乎是一个不必要的约束，可能会减慢训练速度。最后，由于在不同级别使用了相同的噪声，可能会出现一些视觉伪影。相反，如果生成器试图产生自己的伪随机噪声，这种噪音可能看起来不太令人信服，从而导致更多的视觉伪影。另外，生成器的部分权重将专门用于生成伪随机噪声，这似乎又是一种浪费。通过添加额外的噪声输入，可以避免所有这些问题；GAN 能够使用提供的噪声为图像的每个部分添加适量的随机性。

每个级别添加的噪声都不同。每个噪声输入由一个充满高斯噪声的单个特征图组成，该特征图被广播到（给定级别的）所有特征图并使用学习的每个特征缩放因子进行缩放（这由图 17中的“B”框表示） 20 ) 在添加之前。

最后，StyleGAN 使用一种称为混合正则化（或风格混合）的技术，其中一定比例的生成图像是使用两种不同的编码生成的。具体来说，编码c 1和c 2通过映射网络发送，给出两个样式向量w 1和w 2。然后合成网络根据第一层的样式w 1和样式w 2生成图像对于剩余的水平。截止级别是随机选择的。这阻止了网络假设相邻级别的样式是相关的，这反过来又鼓励了 GAN 中的局部性，这意味着每个样式向量仅影响生成图像中有限数量的特征。

GAN 种类繁多，需要一整本书才能涵盖所有内容。希望这个介绍给了你主要的想法，最重要的是，你渴望了解更多。如果您正在为一个数学概念而苦苦挣扎，那么可能有一些博客文章可以帮助您更好地理解它。然后继续实现你自己的 GAN，如果一开始学习有困难，不要气馁：不幸的是，这很正常，需要相当多的耐心才能奏效，但结果是值得的。如果您正在为实现细节而苦恼，可以查看大量 Keras 或 TensorFlow 实现。实际上，如果您只想快速获得一些惊人的结果，那么您可以使用预训练模型（例如，

在下一章中，我们将转向深度学习的一个完全不同的分支：深度强化学习。

练习

1. 自动编码器的主要任务是什么？

2. 假设您想训练一个分类器，并且您有大量未标记的训练数据，但只有几千个标记实例。自动编码器如何提供帮助？你将如何进行？

3. 如果自动编码器完美地重构了输入，它一定是一个好的自动编码器吗？您如何评估自动编码器的性能？

4. 什么是欠完备和过完备自动编码器？过度不完整的自动编码器的主要风险是什么？过完备自动编码器的主要风险是什么？

5. 你如何在堆叠的自动编码器中绑定权重？这样做有什么意义？

6. 什么是生成模型？你能说出一种生成自动编码器的名字吗？

7. 什么是 GAN？你能说出几个 GAN 可以大放异彩的任务吗？

8. 训练 GAN 的主要困难是什么？

9. 尝试使用去噪自动编码器来预训练图像分类器。如果您想要更大的挑战，您可以使用 MNIST（最简单的选项）或更复杂的图像数据集，例如CIFAR10 。无论您使用什么数据集，请按照以下步骤操作：

   • 将数据集拆分为训练集和测试集。在整个训练集上训练深度去噪自动编码器。

   • 检查图像是否重建得相当好。可视化最能激活编码层中每个神经元的图像。

   • 构建分类 DNN，重用自编码器的较低层。仅使用训练集中的 500 张图像对其进行训练。无论有没有预训练，它的表现会更好吗？

10. 在您选择的图像数据集上训练变分自动编码器，并使用它来生成图像。或者，您可以尝试找到您感兴趣的未标记数据集，看看是否可以生成新样本。

11. 训练 DCGAN 来处理您选择的图像数据集，并使用它来生成图像。添加经验回放，看看是否有帮助。将其变成一个条件 GAN，您可以在其中控制生成的类。

附录 A中提供了这些练习的解决方案。

1威廉 G. 蔡斯和赫伯特 A. 西蒙，“国际象棋感知”，认知心理学4，第 4 期。1 (1973): 55–81。

2您可能很想使用准确度指标，但它无法正常工作，因为该指标要求每个像素的标签为 0 或 1。您可以通过创建自定义指标来轻松解决此问题，该指标在将目标和预测四舍五入为 0 或 1 后计算准确度。

3Yoshua Bengio 等人，“深度网络的贪婪层级训练” ，第 19 届神经信息处理系统国际会议论文集（2006 年）：153-160。

4Jonathan Masci 等人，“用于分层特征提取的堆叠卷积自动编码器” ，第 21 届人工神经网络国际会议论文集1（2011 年）：52-59。

5Pascal Vincent 等人，“Extracting and Composing Robust Features with Denoising Autoencoders” ，第 25 届机器学习国际会议论文集（2008 年）：1096-1103。

6Pascal Vincent 等人，“Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion” ，机器学习研究杂志11（2010）：3371–3408。

7Diederik Kingma 和 Max Welling，“自动编码变分贝叶斯”，arXiv 预印本 arXiv:1312.6114 (2013)。

8变分自编码器实际上更通用。编码不限于高斯分布。

9有关更多数学细节，请查看关于变分自动编码器的原始论文，或 Carl Doersch 的精彩教程(2016)。

10Ian Goodfellow 等人，“生成对抗网络” ，第 27 届神经信息处理系统国际会议论文集2（2014 年）：2672-2680。

11要对主要的 GAN 损失进行很好的比较，请查看Hwalsuk Lee 的这个伟大的 GitHub 项目。

12Mario Lucic 等人，“GAN 是否生而平等？一项大规模研究，”第 32 届神经信息处理系统国际会议论文集（2018 年）：698-707。

13Alec Radford 等人，“使用深度卷积生成对抗网络的无监督表示学习”，arXiv 预印本 arXiv:1511.06434 (2015)。

14经作者善意授权转载。

15Mehdi Mirza 和 Simon Osindero，“条件生成对抗网络”，arXiv 预印本 arXiv:1411.1784 (2014)。

16Tero Karras 等人，“GAN 的渐进式增长以提高质量、稳定性和变异性” ，国际学习表示会议论文集（2018 年）。

17变量的动态范围是它可能取的最高值和最低值之间的比率。

18Tero Karras 等人，“A Style-Based Generator Architecture for Generative Adversarial Networks”，arXiv 预印本 arXiv:1812.04948 (2018)。