损失函数汇总
· 0-1损失:
· 平方损失:
· 绝对值损失:
![]()
· hinge loss:
![]()
· 交叉熵损失:
· focal loss:
![]()
在one-stage检测算法中,会出现正负样本数量不平衡以及难易样本数量不平衡的情况,为了解决则以问题提出了focal loss。
hit的检测框就是正样本。容易的正样本是指置信度高且hit的检测框,困难的正样本就是置信度低但hit的检测框,容易的负样本是指未hit且置信度低的检测框,困难的负样本指未hit但置信度高的检测框(hit指预测框和gt框iou是否大于设定的阈值)。
· arcface loss:
· SSIM (Structural SIMilarity) 结构相似性:
SSIM公式基于样本和之间的三个比较衡量:亮度 (luminance)、对比度 (contrast) 和结构 (structure)。
基本不等式: ![]()
施瓦茨不等式:![]()
μ_为均值,δ_为方差,δ_ _协方差,c为常数,避免除0;
![]()
每次计算的时候都从图片上取一个N*N的窗口,然后不断滑动窗口进行计算,最后取平均值作为全局的 SSIM。
# im1 和 im2 都为灰度图像,uint8 类型
ssim = skimage.measure.compare_ssim(im1, im2, data_range=255)附工具链接:
scikit-image
· PSNR (Peak Signal-to-Noise Ratio) 峰值信噪比:
给定一个大小为m*n的干净图像I和噪声图像K,均方误差MSE定义为:
PSNR定义为:
![]() 为图片可能的最大像素值。如果每个像素都由 8 位二进制来表示,那么就为 255;
为图片可能的最大像素值。如果每个像素都由 8 位二进制来表示,那么就为 255;
上面是针对灰度图像的计算方法,如果是彩色图像,通常有三种方法来计算(其中,第二和第三种方法比较常见):
· 分别计算 RGB 三个通道的 PSNR,然后取平均值;
· 计算 RGB 三通道的 MSE ,然后再除以 3 ;
· 将图片转化为 YCbCr 格式,然后只计算 Y 分量也就是亮度分量的 PSNR;
# im1 和 im2 都为灰度图像,uint8 类型
# method 1
diff = im1 - im2
mse = np.mean(np.square(diff))
psnr = 10 * np.log10(255 * 255 / mse)
# method 2
psnr = skimage.measure.compare_psnr(im1, im2, 255)· L1、L2、smooth L1:
![]()
![]()
smooth L1 loss的优势:
当预测框与ground truth差别过大时,梯度不至于过大;
当预测框与ground truth差别很小时,梯度值可足够小;
· IOU loss:
四点回归存在问题:
通过4个点回归坐标框的方式是假设4个坐标点是相互独立的,没有考虑其相关性,实际4个坐标点具有一定的相关性;不具有尺度不变形;可能存在相同的l1 或 l2 loss(如下图),但是IOU不唯一。
IOU loss解决的问题:
尺度不变性,也就是对尺度不敏感(scale invariant), 在regression任务中,判断predict box和gt的距离最直接的指标就是IoU。(满足非负性;同一性;对称性;三角不等性)。
· GIOU loss:
![]() 表示两个框的最小外接矩形
表示两个框的最小外接矩形
IOU loss存在的问题:
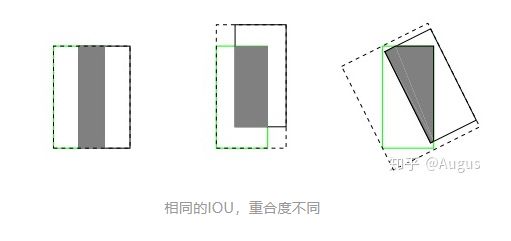
如果两个框没有相交,根据定义,IoU=0,不能反映两者的距离大小(重合度)。同时因为loss=0,没有梯度回传,无法进行学习训练。IoU无法精确的反映两者的重合度大小。如下图所示,三种情况IoU都相等,但看得出来他们的重合度是不一样的,左边的图回归的效果最好,右边的最差。
GIOU loss解决的问题:
尺度不变性、边框相交时,可以反映边框的相交情况。
· DIOU loss:
![]()
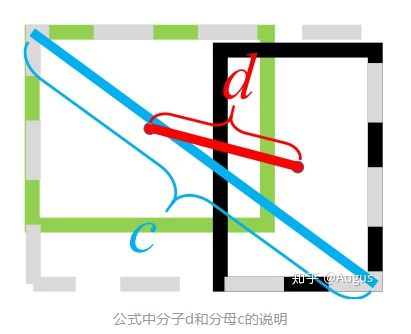
![]() 表示下图中的d,下图c表示两框最小外接矩形对角线长度
表示下图中的d,下图c表示两框最小外接矩形对角线长度
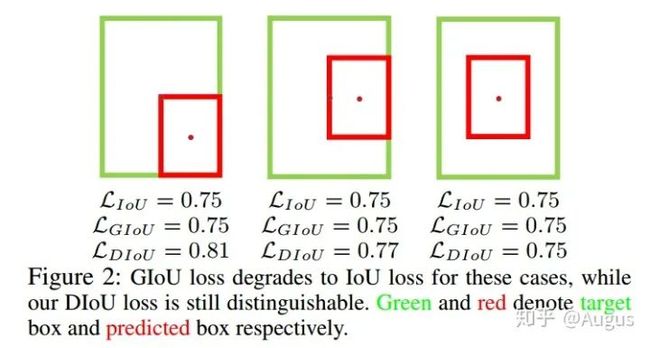
GIOU存在的问题:
只要x和y有一个对上gt、或者预测框包含gt,那GIOU loss就退化成了IOU loss;
DIOU loss解决的问题:
尺度不变性
相比于GIOU,优化距离替换优化面积,收敛速度更快。
解决GIOU的缺点:完全包裹预测框时loss一样的情况。
· CIOU loss:
![]()
DIOU存在的问题:
DIOU没有考虑到检测框的长宽比。长宽比更接近的边框应当有更低的loss。
CIOU解决的问题:
加入检测框的长宽比;
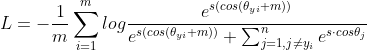
![MSE = \frac{1}{mn}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1}[I(i, j)-K(i,j)]^2](http://img.e-com-net.com/image/info8/28565599497947eab29311e25b1b09b3.gif)