【Machine Learning】4.特征缩放和学习率
特征缩放和学习率
- 1.导入
-
- 1.1 导入包
- 1.2 导入数据集并可视化
- 2.梯度下降
- 3.学习率的选择
- 4.特征缩放
-
- 4.1 z-score normalization
- 4.2.预测
- 4.3 代价等高线 cost contours
本节主要介绍如何处理多个特征,以及怎么调整多元线性回归时的学习率 α \alpha α
1.导入
1.1 导入包
import numpy as np
np.set_printoptions(precision=2)
import matplotlib.pyplot as plt
dlblue = '#0096ff'; dlorange = '#FF9300'; dldarkred='#C00000'; dlmagenta='#FF40FF'; dlpurple='#7030A0';
plt.style.use('./deeplearning.mplstyle')
from lab_utils_multi import load_house_data, compute_cost, run_gradient_descent
from lab_utils_multi import norm_plot, plt_contour_multi, plt_equal_scale, plot_cost_i_w
1.2 导入数据集并可视化
导入数据集
# load the dataset
X_train, y_train = load_house_data()
X_features = ['size(sqft)','bedrooms','floors','age']
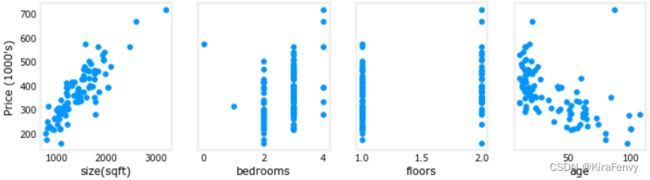
可视化,绘制每个特征和目标值的对比图,可以观察哪个特征的影响更大
fig,ax=plt.subplots(1, 4, figsize=(12, 3), sharey=True)
for i in range(len(ax)):
ax[i].scatter(X_train[:,i],y_train)
ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("Price (1000's)")
plt.show()
2.梯度下降
Here are the equations you developed in the last lab on gradient descent for multiple variables.:
repeat until convergence: { w j : = w j − α ∂ J ( w , b ) ∂ w j for j = 0..n-1 b : = b − α ∂ J ( w , b ) ∂ b } \begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\; & w_j := w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{1} \; & \text{for j = 0..n-1}\newline &b\ \ := b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{align*} repeat} until convergence:{wj:=wj−α∂wj∂J(w,b)b :=b−α∂b∂J(w,b)for j = 0..n-1(1)
where, n is the number of features, parameters w j w_j wj, b b b, are updated simultaneously and where
∂ J ( w , b ) ∂ w j = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) ∂ J ( w , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) \begin{align} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \tag{2} \\ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{3} \end{align} ∂wj∂J(w,b)∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))xj(i)=m1i=0∑m−1(fw,b(x(i))−y(i))(2)(3)
-
m is the number of training examples in the data set
-
f w , b ( x ( i ) ) f_{\mathbf{w},b}(\mathbf{x}^{(i)}) fw,b(x(i)) is the model’s prediction, while y ( i ) y^{(i)} y(i) is the target value
具体理论和代码实现在【Machine Learning】3.多元线性回归 所说过
3.学习率的选择
学习率太大会无法收敛到最优值,学习率太小收敛速度慢,因此要选择一个恰当的学习率
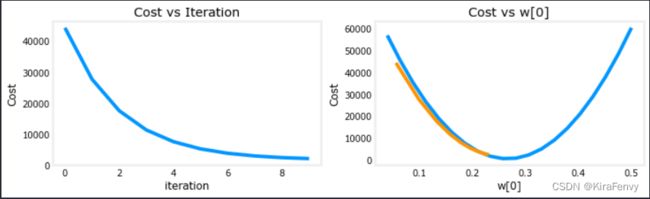
学习率太大时的图像
这个图像的代价甚至是在增长,说明学习率大得离谱

这个图像摆动幅度太大,收敛慢
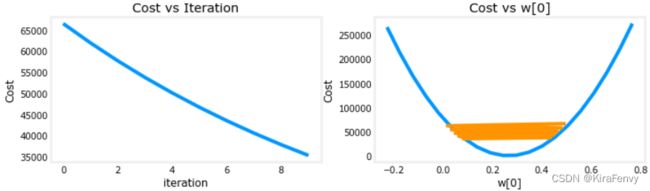
收敛速度合适的图像
4.特征缩放
三种技术:
- Feature scaling 特征缩放, essentially dividing each feature by a user selected value to result in a range between -1 and 1.
- Mean normalization 均值标准化: x i : = x i − μ i m a x − m i n x_i := \dfrac{x_i - \mu_i}{max - min} xi:=max−minxi−μi
- Z-score normalization which we will explore below. Z-score归一化
4.1 z-score normalization
After z-score normalization, all features will have a mean of 0 and a standard deviation of 1. 处理之后,特征平均值为0,标准差为1
x j ( i ) = x j ( i ) − μ j σ j (4) x^{(i)}_j = \dfrac{x^{(i)}_j - \mu_j}{\sigma_j} \tag{4} xj(i)=σjxj(i)−μj(4)
where j j j selects a feature or a column in the X matrix. µ j µ_j µj is the mean of all the values for feature (j) and σ j \sigma_j σj is the standard deviation of feature (j).
μ j = 1 m ∑ i = 0 m − 1 x j ( i ) σ j 2 = 1 m ∑ i = 0 m − 1 ( x j ( i ) − μ j ) 2 \begin{align} \mu_j &= \frac{1}{m} \sum_{i=0}^{m-1} x^{(i)}_j \tag{5}\\ \sigma^2_j &= \frac{1}{m} \sum_{i=0}^{m-1} (x^{(i)}_j - \mu_j)^2 \tag{6} \end{align} μjσj2=m1i=0∑m−1xj(i)=m1i=0∑m−1(xj(i)−μj)2(5)(6)
Implementation Note: 记得把均值和方差标准差存储到变量当中
def zscore_normalize_features(X):
"""
computes X, zcore normalized by column
Args:
X (ndarray): Shape (m,n) input data, m examples, n features
Returns:
X_norm (ndarray): Shape (m,n) input normalized by column
mu (ndarray): Shape (n,) mean of each feature
sigma (ndarray): Shape (n,) standard deviation of each feature
"""
# find the mean of each column/feature
mu = np.mean(X, axis=0) # mu will have shape (n,)
# find the standard deviation of each column/feature
sigma = np.std(X, axis=0) # sigma will have shape (n,)
# element-wise, subtract mu for that column from each example, divide by std for that column
X_norm = (X - mu) / sigma
return (X_norm, mu, sigma)
#check our work
#from sklearn.preprocessing import scale
#scale(X_orig, axis=0, with_mean=True, with_std=True, copy=True)
绘图表示处理过程:
mu = np.mean(X_train,axis=0)
sigma = np.std(X_train,axis=0)
X_mean = (X_train - mu)
X_norm = (X_train - mu)/sigma
fig,ax=plt.subplots(1, 3, figsize=(12, 3))
ax[0].scatter(X_train[:,0], X_train[:,3])
ax[0].set_xlabel(X_features[0]); ax[0].set_ylabel(X_features[3]);
ax[0].set_title("unnormalized")
ax[0].axis('equal')
ax[1].scatter(X_mean[:,0], X_mean[:,3])
ax[1].set_xlabel(X_features[0]); ax[0].set_ylabel(X_features[3]);
ax[1].set_title(r"X - $\mu$")
ax[1].axis('equal')
ax[2].scatter(X_norm[:,0], X_norm[:,3])
ax[2].set_xlabel(X_features[0]); ax[0].set_ylabel(X_features[3]);
ax[2].set_title(r"Z-score normalized")
ax[2].axis('equal')
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
fig.suptitle("distribution of features before, during, after normalization")
plt.show()
- 左:未规范化:“大小(平方英尺)”特征的值范围或方差比年龄大得多
- 中间:第一步从每个特征中减去平均值。这会留下以零为均值的特征。很难看出“年龄”特征的差异,但“大小(平方英尺)”显然约为零。
- 右:第二步除以方差。这将使两个要素以类似的比例居中于零。
计算并存储均值和标准差:
# normalize the original features
X_norm, X_mu, X_sigma = zscore_normalize_features(X_train)
print(f"X_mu = {X_mu}, \nX_sigma = {X_sigma}")
print(f"Peak to Peak range by column in Raw X:{np.ptp(X_train,axis=0)}")
print(f"Peak to Peak range by column in Normalized X:{np.ptp(X_norm,axis=0)}")
X_mu = [1.42e+03 2.72e+00 1.38e+00 3.84e+01],
X_sigma = [411.62 0.65 0.49 25.78]
Peak to Peak range by column in Raw X:[2.41e+03 4.00e+00 1.00e+00 9.50e+01]
Peak to Peak range by column in Normalized X:[5.85 6.14 2.06 3.69]
绘制归一化前和归一化后的各个特征的分布
fig,ax=plt.subplots(1, 4, figsize=(12, 3))
for i in range(len(ax)):
norm_plot(ax[i],X_train[:,i],)
ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("count");
fig.suptitle("distribution of features before normalization")
plt.show()
fig,ax=plt.subplots(1,4,figsize=(12,3))
for i in range(len(ax)):
norm_plot(ax[i],X_norm[:,i],)
ax[i].set_xlabel(X_features[i])
ax[0].set_ylabel("count");
fig.suptitle(f"distribution of features after normalization")
plt.show()
w_norm, b_norm, hist = run_gradient_descent(X_norm, y_train, 1000, 1.0e-1, )
请注意,使用标准化特征进行预测,而使用原始特征值显示绘图。
#predict target using normalized features
m = X_norm.shape[0]
yp = np.zeros(m)
for i in range(m): #使用标准化特征预测
yp[i] = np.dot(X_norm[i], w_norm) + b_norm
# plot predictions and targets versus original features
fig,ax=plt.subplots(1,4,figsize=(12, 3),sharey=True)
for i in range(len(ax)):
ax[i].scatter(X_train[:,i],y_train, label = 'target') #使用原始特征值绘图
ax[i].set_xlabel(X_features[i])
ax[i].scatter(X_train[:,i],yp,color=dlorange, label = 'predict')
ax[0].set_ylabel("Price"); ax[0].legend();
fig.suptitle("target versus prediction using z-score normalized model")
plt.show()
4.2.预测
预测的时候也要将输入数据进行归一化
# First, normalize out example.
x_house = np.array([1200, 3, 1, 40])
x_house_norm = (x_house - X_mu) / X_sigma
print(x_house_norm)
x_house_predict = np.dot(x_house_norm, w_norm) + b_norm
print(f" predicted price of a house with 1200 sqft, 3 bedrooms, 1 floor, 40 years old = ${x_house_predict*1000:0.0f}")
[-0.53 0.43 -0.79 0.06]
predicted price of a house with 1200 sqft, 3 bedrooms, 1 floor, 40 years old = $318709
4.3 代价等高线 cost contours
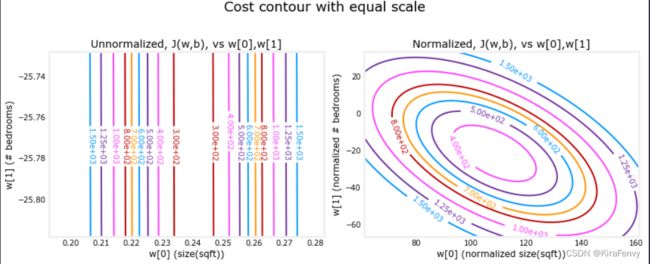
当特征比例不匹配时,等高线图中成本与参数的关系图是不对称的。
在下图中,参数的比例是匹配的。左边的图是w[0]的成本等值线图,平方英尺与w[1]的对比,是特征正常化之前的卧室数量。图是如此不对称,完成轮廓的曲线是不可见的。相比之下,当特征归一化时,成本轮廓更加对称。结果是,梯度下降期间的参数更新可以使每个参数的进度相等。