9.20残差网络 ResNet
- 现在经常使用的网络之一
问题:随着神经网络的不断加深,一定会带来好处吗?
- 不一定。
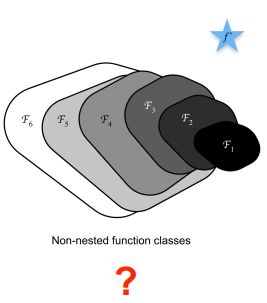
- 蓝色五角星表示最优值
- 标有Fi的闭合区域表示函数,闭合区域的面积代表函数的复杂程度,在这个区域中能够找到一个最优的模型(可以用区域中的一个点来表示,该点到最优值的距离可以用来衡量模型的好坏)
- 从上图中可以看出,随着函数的复杂度的不断增加,虽然函数的区域面积增大了,但是在该区域中所能找到的最优模型(该区域内的某一点)离最优值的距离可能会越来越远(也就是模型所在的区域随着函数复杂度的增加,逐渐偏离了原来的区域,离最优值越来越远)(非嵌套函数(non-nested function))
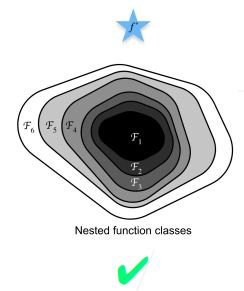
- 解决上述问题(模型走偏)的方法:每一次增加函数复杂度之后函数所覆盖的区域会包含原来函数所在的区域(嵌套函数(nested function)),只有当较复杂的函数类包含复杂度较小的函数类时,才能确保提高它的性能,如下图所示
- 也就是说,增加函数的复杂度只会使函数所覆盖的区域在原有的基础上进行扩充,而不会偏离原本存在的区域
- 对于深度神经网络,如果能将新添加的层训练成恒等映射(identify function)f(x) = x,新模型和原模型将同样有效;同时,由于新模型可能得出更优的解来拟合训练数据集,因此添加层似乎更容易降低训练误差
核心思想
残差网络的核心思想是:每个附加层都应该更容易地包含原始函数作为其元素之一
由此,残差块(residual blocks)诞生了
残差块
- 之前增加模型深度的方法都是层层堆叠的方法,ResNet的思想是在堆叠层数的同时不会增加模型的复杂度
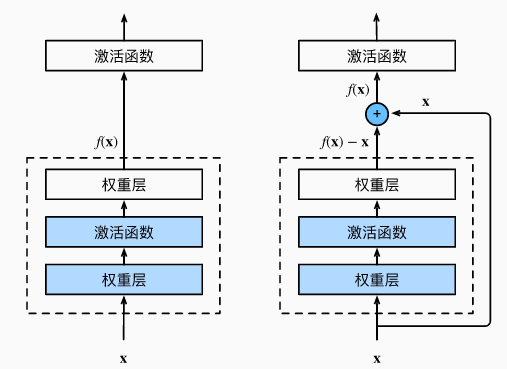
- 上图中左侧表示一个正常块,右侧表示一个残差块
- x:原始输入
- f(x):理想映射(也是激活函数的输入)
- 对于正常块中来说,虚线框中的部分需要直接拟合出理想映射 f(x);而对于残差块来说,同样的虚线框中的部分需要拟合出残差映射 f(x) - x
- 残差映射在现实中往往更容易优化
- 如果以恒等映射 f(x) = x 作为所想要学出的理想映射 f(x),则只需要将残差块中虚线框内加权运算的权重和偏置参数设置为 0,f(x) 就变成恒等映射了
- 在实际中,当理想映射 f(x) 极接近于恒等映射时,残差映射易于捕捉恒等映射的细微波动
- 在残差块中,输入可以通过跨层数据线路更快地向前传播
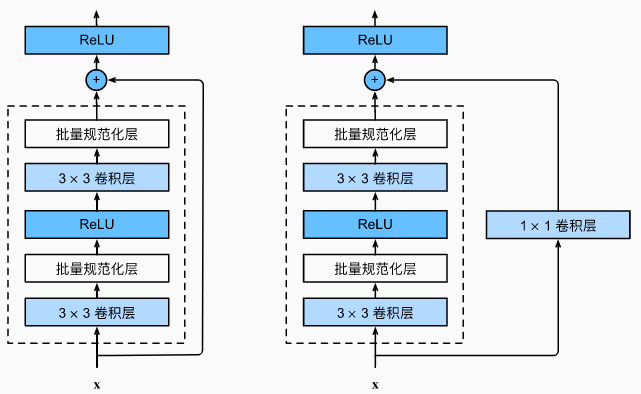
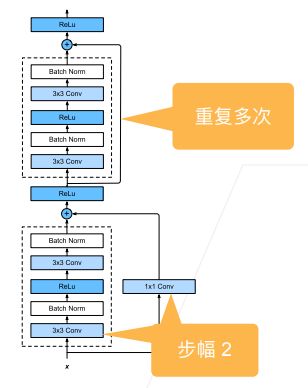
- 左边是ResNet的第一种实现(不包含1 * 1卷积层的残差块),它直接将输入加在了叠加层的输出上面
- 右边是ResNet的第二种实现(包含1 * 1卷积层的残差块),它先对输入进行了1 * 1的卷积变换通道(改变范围),再加入到叠加层的输出上面
- ResNet沿用了VGG完整的3 * 3卷积层设计
- 残差块中首先有2个相同输出通道数的3 * 3卷积层,每个卷积层后面接一个批量归一化层和ReLu激活函数;通过跨层数据通路,跳过残差块中的两个卷积运算,将输入直接加在最后的ReLu激活函数前(这种设计要求2个卷积层的输出与输入形状一样,这样才能使第二个卷积层的输出(也就是第二个激活函数的输入)和原始的输入形状相同,才能进行相加)
- 如果想要改变通道数,就需要引入一个额外的1 * 1的卷积层来将输入变换成需要的形状后再做相加运算(如上图中右侧含1 * 1卷积层的残差块)
不同的残差块
ResNet架构
原本的ResNet和VGG类似,ResNet块有两种:
- 第一种是高宽减半的ResNet块。第一个卷积层的步幅等于2,使得高宽减半,通道数翻倍(如上图下半部分所示)
- 第二种是高宽不减半的RexNet块,如上图上半部分所示,重复多次,所有卷积层的步幅等于1
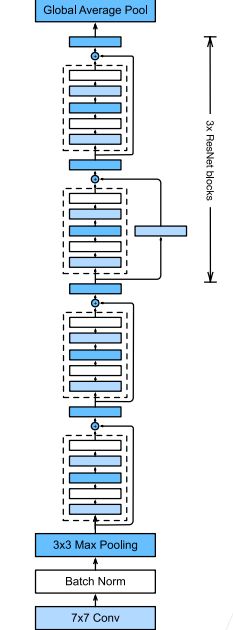
通过ResNet块数量和通道数量的不同,可以得到不同的ResNet架构,ResNet-18架构如下图所示
- ResNet架构类似于VGG和GoogLeNet的总体架构,但是替换成了ResNet块(ResNet块的每个卷积层后增加了批量归一化层)
- ResNet的前两层和GoogLeNet中的一样,也分成了5个stage:在输出通道数为64、步幅为2的7 * 7卷积层后,接步幅为2的3 * 3的最大汇聚层
- GoogLeNet在后面接了4由Inception块组成的模块;ResNet使用了4个由残差块组成的模块,每个模块使用若干个同样输出通道数的残差块,第一个模块的通道数同输入通道数一致;由于之前已经使用了步幅为2的最大汇聚层,所以无需减小高和宽;之后每个模块在第一个残差块里将上一个模块的通道数翻倍,并将高和宽减半
- 通过配置不同的通道数和模块中的残差块数可以得到不同的ResNet模型:ResNet-18:每个模块都有4个卷积层(不包含恒等映射的1 * 1卷积层),再加上第一个7 * 7卷积层和最后一个全连接层,一共有18层;还有更深的152层的ResNet-152
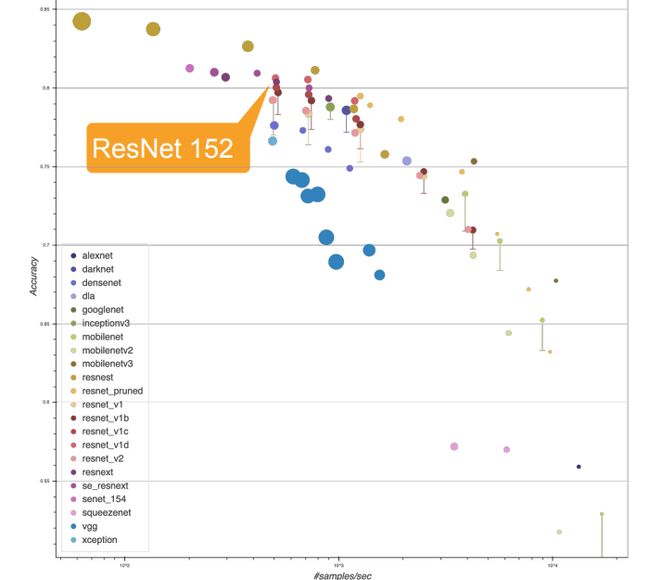
ResNet 152
- 图中所示的是ResNet-152(经过两三次改良之后的版本)在ImageNet数据集上分类任务的精度
- 模型的层数越少通常速度越快,精度越低,层数越多,精度越低
- ResNet 152是一个经常用来刷分的模型,在实际中使用的比较少
总结
- 残差块使得很深的网络更加容易训练(不管网络有多深,因为有跨层数据通路连接的存在,使得始终能够包含小的网络,因为跳转连接的存在,所以会先将下层的小型网络训练好再去训练更深层次的网络),甚至可以训练一千层的网络(只要内存足够,优化算法就能够实现)
- 学习嵌套函数是神经网络的理想情况,在深层神经网络中,学习另一层作为恒等映射比较容易
- 残差映射可以更容易地学习同一函数,例如将权重层中的参数近似为零
- 利用残差块可以训练出一个有效的深层神经网络:输入可以通过层间的残余连接更快地向前传播
- 残差网络对随后的深层神经网络的设计产生了深远影响,无论是卷积类网络还是全连接类网络,几乎现在所有的网络都会用到,因为只有这样才能够让网络搭建的更深
代码:
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual (nn.Module):
def __init__(self, input_channels, num_channels, use_1x1conv=False,strides=1): # num_channels为输出channel数
super().__init__()
self.conv1 = nn.Conv2d(
input_channels, num_channels, kernel_size=3,
padding=1, stride=strides) # 可以使用传入进来的strides
self.conv2 = nn.Conv2d(
num_channels, num_channels, kernel_size=3,
padding=1) # 使用nn.Conv2d默认的strides=1
if use_1x1conv:
self.conv3 = nn.Conv2d(
input_channels, num_channels, kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
self.relu = nn.ReLU(inplace=True) # inplace原地操作,不创建新变量,对原变量操作,节约内存
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)
# 输入和输出形状一致
blk = Residual(3,3) # 输入三通道,输出三通道
X = torch.rand(4,3,6,6)
Y = blk(X) # stride用的默认的1,所以宽高没有变化。如果strides用2,则宽高减半
Y.shape
# 增加输出通道数的同时,减半输出的高和宽
blk = Residual(3,6,use_1x1conv=True,strides=2) # 由3变为6,通道数加倍
blk(X).shape
# ResNet的第一个stage
b1 = nn.Sequential(nn.Conv2d(1,64,kernel_size=7,stride=2,padding=3),
nn.BatchNorm2d(64),nn.ReLU(),
nn.MaxPool2d(kernel_size=3,stride=2,padding=1))
# class Residual为小block,resnet_block 为大block,为Resnet网络的一个stage
def resnet_block(input_channels,num_channels,num_residuals,first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block: # stage中不是第一个block则高宽减半
blk.append(Residual(input_channels, num_channels, use_1x1conv=True,strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64,64,2,first_block=True)) # 因为b1做了两次宽高减半,nn.Conv2d、nn.MaxPool2d,所以b2中的首次就不减半了
b3 = nn.Sequential(*resnet_block(64,128,2)) # b3、b4、b5的首次卷积层都减半
b4 = nn.Sequential(*resnet_block(128,256,2))
b5 = nn.Sequential(*resnet_block(256,512,2))
net = nn.Sequential(b1,b2,b3,b4,b5,nn.AdaptiveAvgPool2d((1,1)),nn.Flatten(),nn.Linear(512,10))
# 观察一下ReNet中不同模块的输入形状是如何变化的
X = torch.rand(size=(1,1,224,224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__,'output shape:\t',X.shape) # 通道数翻倍、模型减半
# 训练模型
lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())