【Java】想进大厂？你应该知道的算法经典习题(链表)

✅作者简介：大家好我是烫嘴的辛拉面，大家可以叫我拉面。
个人主页: 烫嘴的辛拉面的博客
系列专栏： 经典算法习题集
为大推荐一款刷题神器哦 点击跳转进入网站

前言：我将在专栏 经典算法习题集持续更新，整理牛客网经典算法的习题练习，如果感兴趣请关注专栏。牛客网除了算法题单之外还有其他热门的各种提单，应有尽有，大家快刷起来吧点击跳转进入牛客网

✏️链表

✒️AB9 【模板】链表

题目描述

描述
请你实现一个链表。
操作：
insert x y：将yyy加入链表，插入在第一个值为xxx的结点之前。若链表中不存在值为xxx的结点，则插入在链表末尾。保证xxx,yyy为int型整数。
delete x：删除链表中第一个值为xxx的结点。若不存在值为xxx的结点，则不删除。
输入描述：
第一行输入一个整数nnn (1≤n≤1041\le n \le 10^41≤n≤104)，表示操作次数。
接下来的nnn行，每行一个字符串，表示一个操作。保证操作是题目描述中的一种。
输出描述：
输出一行，将链表中所有结点的值按顺序输出。若链表为空，输出"NULL"(不含引号)。
示例1
输入：

5
insert 0 1
insert 0 3
insert 1 2
insert 3 4
delete 4

输出：

2 1 3

解题思路

本题主要进行 在指定位置插入节点 以及 删除指定位置节点 的链表操作的模拟（本题解使用带头节点的链表）

首先在结构体中定义用于存储节点数据的data和用于指向下一个节点的结构体指针next。

对于插入操作，需要在第一次出现指定值的节点之前的位置进行节点的插入，因此需要两个指针，p指针向后遍历链表寻找指定值节点，q指针跟随在p指针之前，以便于新节点的插入。当p指针找到指定值节点或为空时，便new一个新节点，将其插入到q节点之后即可。

对于删除操作，与插入操作类似，依然需要p和q两个指针，当p指针找到指定位置后，将q指针的next指向p指针的next，然后将p指针的next置空，即可delete p，达到删除指定位置节点的要求。

代码实现

![#include<iostream>
using namespace std;
struct List
{
    int data;
    List* next;
};
void insert(List* p, int x, int y) // 在指定位置插入节点
{
    List* q = p;
    p = p->next;
    while(p != NULL)
    {
        if(p->data == x)
        {
            break;
        }
        q = p;
        p = p->next;
    }
    List* t = new List();
    t->data = y;
    q->next = t;
    t->next = p;
}
void del(List* p, int x) // 删除指定位置节点
{
    List* q = p;
    p = p->next;
    while(p != NULL)
    {
        if(p->data == x)
        {
            q->next = p->next;
            p->next = NULL;
            delete p;
            return ;
        }
        q = p
        p = p->next;
    }
}
int main()
{
    int n;
    cin>>n;
    List* head = new List();
    head->next = NULL; // 创建带头节点的链表
    for(int i = 0; i < n; i++)
    {
        string op;
        cin>>op;
        if(op == "insert")
        {
            int x, y;
            cin>>x>>y;
            insert(head, x, y);
        }
        if(op == "delete")
        {
            int x;
            cin>>x;
            del(head, x);
        }
    }
    List* f = head->next; // 因为带头节点，因此需要从head->next开始遍历链表
    if(f == NULL)
    {
        cout<<"NULL";
    }
    while(f != NULL)
    {
        cout<<f->data<<" ";
        f = f->next;
    }
    return 0;
}](https://img-blog.csdnimg.cn/add9259baf0f4a93a3457893856bf80c.png)

✒️AB10 反转链表

题目描述

给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

数据范围： 0≤n≤10000\leq n\leq10000≤n≤1000
要求：空间复杂度 O(1)O(1)O(1) ，时间复杂度 O(n)O(n)O(n) 。

如当输入链表{1,2,3}时，
经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。
以上转换过程如下图所示：

示例1

输入：{1,2,3}
返回值：{3,2,1}

示例2

输入：{}
返回值：{}

说明：

空链表则输出空

解题思路与代码实现

有三种解决方式
1，使用栈解决

链表的反转是老生常谈的一个问题了，同时也是面试中常考的一道题。最简单的一种方式就是使用栈，因为栈是先进后出的。实现原理就是把链表节点一个个入栈，当全部入栈完之后再一个个出栈，出栈的时候在把出栈的结点串成一个新的链表。原理如下
图片说明

import java.util.Stack;
public class Solution {
public ListNode ReverseList(ListNode head) {
    Stack<ListNode> stack= new Stack<>();
    //把链表节点全部摘掉放到栈中
    while (head != null) {
        stack.push(head);
        head = head.next;
    }
    if (stack.isEmpty())
        return null;
    ListNode node = stack.pop();
    ListNode dummy = node;
    //栈中的结点全部出栈，然后重新连成一个新的链表
    while (!stack.isEmpty()) {
        ListNode tempNode = stack.pop();
        node.next = tempNode;
        node = node.next;
    }
    //最后一个结点就是反转前的头结点，一定要让他的next
    //等于空，否则会构成环
    node.next = null;
    return dummy;
}
}

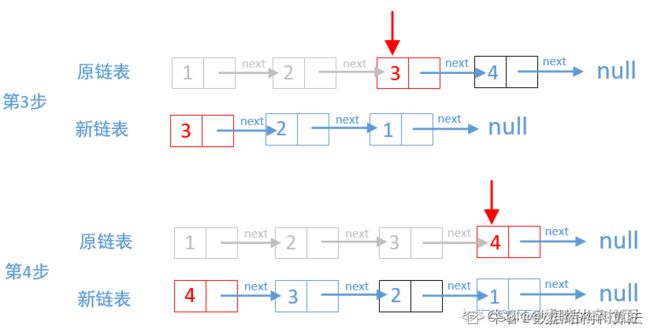
2,双链表求解

双链表求解是把原链表的结点一个个摘掉，每次摘掉的链表都让他成为新的链表的头结点，然后更新新链表。下面以链表1→2→3→4为例画个图来看下。
图片说明

图片说明

他每次访问的原链表节点都会成为新链表的头结点，最后再来看下代码

public ListNode ReverseList(ListNode head) {
    //新链表
    ListNode newHead = null;
    while (head != null) {
        //先保存访问的节点的下一个节点，保存起来
        //留着下一步访问的
        ListNode temp = head.next;
        //每次访问的原链表节点都会成为新链表的头结点，
        //其实就是把新链表挂到访问的原链表节点的
        //后面就行了
        head.next = newHead;
        //更新新链表
        newHead = head;
        //重新赋值，继续访问
        head = temp;
    }
    //返回新链表
    return newHead;
}

3,递归解决

我们再来回顾一下递归的模板，终止条件，递归调用，逻辑处理。
public ListNode reverseList(参数0) {
    if (终止条件)
        return;

    逻辑处理（可能有，也可能没有，具体问题具体分析）

    //递归调用
    ListNode reverse = reverseList(参数1);

    逻辑处理（可能有，也可能没有，具体问题具体分析）
}

终止条件就是链表为空，或者是链表没有尾结点的时候，直接返回

if (head == null || head.next == null)
    return head;

递归调用是要从当前节点的下一个结点开始递归。逻辑处理这块是要把当前节点挂到递归之后的链表的末尾，看下代码

public ListNode ReverseList(ListNode head) {
    //终止条件
    if (head == null || head.next == null)
        return head;
    //保存当前节点的下一个结点
    ListNode next = head.next;
    //从当前节点的下一个结点开始递归调用
    ListNode reverse = ReverseList(next);
    //reverse是反转之后的链表，因为函数reverseList
    // 表示的是对链表的反转，所以反转完之后next肯定
    // 是链表reverse的尾结点，然后我们再把当前节点
    //head挂到next节点的后面就完成了链表的反转。
    next.next = head;
    //这里head相当于变成了尾结点，尾结点都是为空的，
    //否则会构成环
    head.next = null;
    return reverse;
}

因为递归调用之后head.next节点就会成为reverse节点的尾结点，我们可以直接让head.next.next = head;，这样代码会更简洁一些，看下代码

public ListNode ReverseList(ListNode head) {
    if (head == null || head.next == null)
        return head;
    ListNode reverse = ReverseList(head.next);
    head.next.next = head;
    head.next = null;
    return reverse;
}

这种递归往下传递的时候基本上没有逻辑处理，当往回反弹的时候才开始处理，也就是从链表的尾端往前开始处理的。我们还可以再来改一下，在链表递归的时候从前往后处理，处理完之后直接返回递归的结果，这就是所谓的尾递归，这种运行效率要比上一种好很多

public ListNode ReverseList(ListNode head) {
    return reverseListInt(head, null);
}

private ListNode reverseListInt(ListNode head, ListNode newHead) {
    if (head == null)
        return newHead;
    ListNode next = head.next;
    head.next = newHead;
    return reverseListInt(next, head);
}

尾递归虽然也会不停的压栈，但由于最后返回的是递归函数的值，所以在返回的时候都会一次性出栈，不会一个个出栈这么慢。但如果我们再来改一下，像下面代码这样又会一个个出栈了

public ListNode ReverseList(ListNode head) {
    return reverseListInt(head, null);
}

private ListNode reverseListInt(ListNode head, ListNode newHead) {
    if (head == null)
        return newHead;
    ListNode next = head.next;
    head.next = newHead;
    ListNode node = reverseListInt(next, head);
    return node;
}

✒️AB11 合并两个排序的链表

题目描述

输入两个递增的链表，单个链表的长度为n，合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围： 0≤n≤10000 \le n \le 10000≤n≤1000，−1000≤节点值≤1000-1000 \le 节点值 \le 1000−1000≤节点值≤1000
要求：空间复杂度 O(1)O(1)O(1)，时间复杂度 O(n)O(n)O(n)

如输入{1,3,5},{2,4,6}时，合并后的链表为{1,2,3,4,5,6}，所以对应的输出为{1,2,3,4,5,6}，转换过程如下图所示：

或输入{-1,2,4},{1,3,4}时，合并后的链表为{-1,1,2,3,4,4}，所以对应的输出为{-1,1,2,3,4,4}，转换过程如下图所示：

示例1

输入：{1,3,5},{2,4,6}
返回值：{1,2,3,4,5,6}

示例2

输入：{},{}
返回值：{}

示例3

输入：{-1,2,4},{1,3,4}
返回值：{-1,1,2,3,4,4}

解题思路

方法一：迭代版本求解

初始化：定义cur指向新链表的头结点
操作：

如果l1指向的结点值小于等于l2指向的结点值，则将l1指向的结点值链接到cur的next指针，然后l1指向下一个结点值
否则，让l2指向下一个结点值
循环步骤1,2，直到l1或者l2为nullptr
将l1或者l2剩下的部分链接到cur的后面 

方法二：递归版本

方法一的迭代版本，很好理解，代码也好写。但是有必要介绍一下递归版本，可以练习递归代码。
写递归代码，最重要的要明白递归函数的功能。可以不必关心递归函数的具体实现。
比如这个ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
函数功能：合并两个单链表，返回两个单链表头结点值小的那个节点。

如果知道了这个函数功能，那么接下来需要考虑2个问题：

递归函数结束的条件是什么？
递归函数一定是缩小递归区间的，那么下一步的递归区间是什么？
对于问题1.对于链表就是，如果为空，返回什么
对于问题2，跟迭代方法中的一样，如果PHead1的所指节点值小于等于pHead2所指的结点值，那么phead1后续节点和pHead节点继续递归

代码实现

方法一：迭代版本求解

class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
    {
        ListNode *vhead = new ListNode(-1);
        ListNode *cur = vhead;
        while (pHead1 && pHead2) {
            if (pHead1->val <= pHead2->val) {
                cur->next = pHead1;
                pHead1 = pHead1->next;
            }
            else {
                cur->next = pHead2;
                pHead2 = pHead2->next;
            }
            cur = cur->next;
        }
        cur->next = pHead1 ? pHead1 : pHead2;
        return vhead->next;
    }
};

方法二：递归版本

class Solution {
public:
 ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
 {
     if (!pHead1) return pHead2;
     if (!pHead2) return pHead1;
     if (pHead1->val <= pHead2->val) {
         pHead1->next = Merge(pHead1->next, pHead2);
         return pHead1;
     }
     else {
         pHead2->next = Merge(pHead1, pHead2->next);
         return pHead2;
     }
 }
};

✒️AB12 删除链表的节点

题目描述

给定单向链表的头指针和一个要删除的节点的值，定义一个函数删除该节点。返回删除后的链表的头节点。
1.此题对比原题有改动
2.题目保证链表中节点的值互不相同
3.该题只会输出返回的链表和结果做对比，所以若使用 C 或 C++ 语言，你不需要 free 或 delete 被删除的节点

数据范围:
0<=链表节点值<=10000
0<=链表长度<=10000
示例1

输入：{2,5,1,9},5
返回值：{2,1,9}
说明：给定你链表中值为 5 的第二个节点，那么在调用了你的函数之后，该链表应变为 2 -> 1 -> 9

示例2

输入：{2,5,1,9},1
返回值：{2,5,9}
说明：给定你链表中值为 1 的第三个节点，那么在调用了你的函数之后，该链表应变为 2 -> 5 -> 9

解题思路

既然是整个链表元素都不相同，我们要删除给定的一个元素，那我们首先肯定要找到这个元素，然后考虑删除它。

删除一个链表节点，肯定是断掉它的前一个节点指向它的指针，然后指向它的后一个节点，即越过了需要删除的这个节点。

step 1：首先我们加入一个头部节点，方便于如果可能的话删除掉第一个元素。
step 2：准备两个指针遍历链表，一个指针指向当前要遍历的元素，另一个指针指向该元素的前序节点，便于获取它的指针。
step 3：遍历链表，找到目标节点，则断开连接，指向后一个。
step 4：返回时去掉我们加入的头节点。

图示：

代码实现

import java.util.*;
public class Solution {
    public ListNode deleteNode (ListNode head, int val) {
        //加入一个头节点
        ListNode res = new ListNode(0);
        res.next = head;
        //前序节点
        ListNode pre = res;
        //当前节点
        ListNode cur = head;
        //遍历链表
        while(cur != null){
            //找到目标节点
            if(cur.val == val){
                //断开连接
                pre.next = cur.next;
                break;
            }
            pre = cur;
            cur = cur.next;
        }
        //返回去掉头节点
        return res.next;
    }
}