深度学习与计算机视觉教程(18) | 深度强化学习 (梯度策略,Actor-Critic,DDPG,A3C)（CV通关指南·完结）

• 作者：韩信子@ShowMeAI
• 教程地址：https://www.showmeai.tech/tutorials/37
• 本文地址：https://www.showmeai.tech/article-detail/277
• 声明：版权所有，转载请联系平台与作者并注明出处
• 收藏ShowMeAI查看更多精彩内容

---

本系列为 斯坦福CS231n 《深度学习与计算机视觉(Deep Learning for Computer Vision)》的全套学习笔记，对应的课程视频可以在 这里 查看。更多资料获取方式见文末。

---

引言

前一篇ShowMeAI的文章 深度学习与计算机视觉教程(17) | 深度强化学习 (马尔可夫决策过程, Q-Learning, DQN) 中，我们学习了Q-Learning 系列方法，它是基于价值（value-based）的方法， 也就是通过计算每一个状态动作的价值，然后选择价值最大的动作执行。

这是一种间接的强化学习建模做法，另外一类policy-based方法会直接更新策略。本篇我们将顺着这条主线给大家介绍Policy Gradient等方法，当然，强化学习中还有结合policy-based 和 value-based 的 Actor-Critic 方法，以及在 Actor-Critic 基础上的 DDPG、A3C方法。

本篇重点

• Policy Gradient 算法
• Actor-Critic 算法
• DDPG 算法
• A3C 算法

1.Policy Gradient算法

1.1 算法介绍

Policy Gradient 是最基础的强化学习算法之一，它通过更新 策略网络/Policy Network 来直接更新策略的。Policy Network 是一个神经网络，输入是状态，输出直接就是动作（不是Q值） ，且一般输出有两种方式：

• ① 概率的方式，即输出某一个动作的概率。
• ② 确定性的方式，即输出具体的某一个动作。

如果要更新 Policy Network 策略网络，或者说要使用梯度下降的方法来更新网络，需要有一个目标函数，对于所有强化学习的任务来说，最终目标都是使所有累加reward/奖励（带衰减）最大。如下公式所示：

$$L(\theta )=\mathbb{E}(r_1+\gamma r_2+{\gamma }^2{r}_3+\dots \mid \pi (,\theta ))$$

但上述损失函数和 Policy Network 策略网络无法直接关联：reward 是环境给出的，无法基于参数 $\theta$ 计算得到。假如我们后续优化还是基于「梯度下降」等算法，那损失函数关于参数的梯度 ${\nabla }_{\theta }L(\theta )$ 如何得到呢？

我们换一个思路来考虑：假如我们现在有一个策略网络，输入状态，输出动作的概率。然后执行完动作之后，我们可以得到 reward，或者 result。

我们可以采取1个非常直观简单的做法：增大得到 reward 多的动作的输出概率，减小得到 reward 少的动作的输出概率。

但是大家可能会注意到：用 reward 或 result 来评判动作好坏可能是不准确的（因为任何一个 reward，result 都依赖于大量的动作才导致的，不能只将功劳或过错归于当前的动作上）。

我们的处理思路改为：我们构造一个判断动作好坏的「评判指标」，再通过改变动作的出现概率来优化策略！

假设这个评价指标是 $f(s,a)$，我们的策略网络输出的 $\pi (a|s,\theta )$ 是概率，那么可以通过极大似然估计的方法来优化这个目标。比如说我们可以构造如下目标函数：

$$L(\theta )=\sum log\pi (a|s,\theta )f(s,a)$$

举例来说，对某场游戏来说，假如最终赢了，那么认为这局游戏中每一步都是好的，如果输了，那么认为都是不好的。好的 $f(s,a)$ 就是 $1$，不好的就是 $-1$，然后极大化上面的目标函数即可。

实际上，除了极大化上面的目标函数，还可以直接对 $f(s,a)$ 进行极大化，如这篇博文 Deep Reinforcement Learning: Pong from Pixels 中直接最大化 $f(x)$ 也就是 $f(s,a)$ 的期望，可以看到，最后的结果跟上面的目标函数是一致的。

$$\begin{array}{rlr}{\nabla }_{\theta }{E}_x[f(x)]& ={\nabla }_{\theta }\sum _{x}p(x)f(x)& \text{ 定义期望 }\\ & =\sum _x{\nabla }_{\theta }p(x)f(x)& \text{ 把「求和」挪至前方 }\\ & =\sum _{x}p(x)\frac{{\nabla }_{\theta }p(x)}{p(x)}f(x)& \text{ 公式变化，乘除 }p(x)\\ & =\sum _{x}p(x){\nabla }_{\theta }\log p(x)f(x)& \text{ 基于求导公式 }{\nabla }_{\theta }\log (z)=\frac{1}{z}{\nabla }_{\theta }z\\ & =E_x\left[f(x){\nabla }_{\theta }\log p(x)\right]& \text{期望的定义}\end{array}$$

1.2 PG评判指标的选择

从上文中可以看出来，Policy Gradient 中评价指标 $f(s,a)$ 的定义是关键。 我们前面提到的「根据回合的输赢来判断这个回合中的每1步好坏」的方式比较粗糙简单。但其实我们更希望每走1步就能够获取到这一步的具体评价，因此出现了很多其他的直接给出某个时刻的评估的评价方式。如这篇论文 High-dimensional continuous control using generalized advantage estimation 里就对比了若干种 PG 评价指标。

1.3 梯度策略算法总结

借用 David Silver 老师讲解梯度策略算法时候的一页核心 PPT 内容，翻译作为梯度策略算法的总结。Policy gradient 通过不断重复估测梯度 $g:={\nabla }_{\theta }\mathbb{E}\left[{\sum }_{t=0}^{\infty }{r}_t\right]$ 来最大化期望收益，有几种不同的梯度策略形式，我们可以统一写成：

$$g=\mathbb{E}\left[\sum _{t=0}^{\infty }{\Psi }_t{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right)\right]$$

上面公式中的 ${\Psi }_t$ 就是 $t$ 时刻的评价指标。它可能是如下的形态：

• ① ${\sum }_{t=0}^{\infty }{r}_t$：整个过程总体 reward 收益

• ② ${\sum }_{t^{\prime }=t}^{\infty }{r}_{t^{\prime }}$：动作 $a_t$ 之后的收益

• ③ ${\sum }_{t^{\prime }=t}^{\infty }{r}_{t^{\prime }}-b\left(s_t\right)$：前序公式的基线版本

• ④ $Q^{\pi }\left(s_t,a_t\right)$：state-action价值函数

• ⑤ $A^{\pi }\left(s_t,a_t\right)$：advantage function/优势函数

• ⑥ $r_t+V^{\pi }\left(s_{t+1}\right)-V^{\pi }\left(s_t\right)$ ：TD residual/时序差分残差

更具体的一些公式如下：

$$V^{\pi }\left(s_t\right):=\mathbb{E}{s}_{t+1:\infty },\left[\sum _{l=0}^{\infty }{r}_{t+l}\right]$$

$$Q^{\pi }\left(s_t,a_t\right):={\mathbb{E}}_{a_{t+1:\infty }}^{a_{t+1:\infty }}\left[\sum _{l=0}^{\infty }{r}_{t+l}\right]$$

$$A^{\pi }\left(s_t,a_t\right):=Q^{\pi }\left(s_t,a_t\right)-V^{\pi }\left(s_t\right)(Advantagefunction)$$

在梯度策略里我们可以使用 reward，使用 $Q$、$A$ 或者 $TD$ 来作为动作的评价指标。这些方法的本质区别在于 variance 和 bias 的问题：

用 reward 来作为动作的评价：

• 这样做 bias 比较低，不过 variance 很大，reward 值太不稳定，训练可能不收敛。

采用 $Q$ 值的方法：

• 因为 $Q$ 值是对 reward 的期望值，使用 $Q$ 值 variance 比较小，bias 比较大。一般我们会选择使用 $A$，Advantage。$A=Q-V$，是一个动作相对当前状态的价值。本质上 $V$ 可以看做是baseline。对于上面 ③ 的公式，也可以直接用 $V$ 来作为 baseline。
• 但是还是一样的问题，$A$ 的 variance 比较大。为了平衡 variance 和 bias 的问题，使用 $TD$ 会是比较好的做法，既兼顾了实际值 reward，又使用了估计值 $V$。在 $TD$ 中，$TD(lambda)$ 平衡不同长度的 $TD$ 值，会是比较好的做法。

在实际使用中，需要根据具体的问题选择不同的方法。有的问题 reward 很容易得到，有的问题 reward 非常稀疏。reward 越稀疏，也就越需要采用估计值。

总结一下 Policy Gradient 的核心思想：

通过 policy network 输出的 Softmax 概率 和获取的 reward （通过评估指标获取）构造目标函数，然后对 policy network 进行更新。

梯度策略避免了原来的 reward 和 policy network 之间是不可微的问题。也因为它这个特点，目前的很多传统监督学习的问题因为输出都是 Softmax 的离散形式，都可以改造成 Policy Gradient 的方法来实现，调节得当效果会在监督学习的基础上进一步提升。

2.Actor-Critic算法

在 policy gradient 中讲解到的多种评估指标已经涵盖了下面要介绍的 Actor-Critic 的思想，梯度策略算法往往采用回合更新的模式，即每轮结束后才能进行更新。

如某盘游戏，假如最后的结果是胜利了，那么可以认为其中的每一步都是好的，反之则认为其中的每一步都是不好的。

下图摘自 David Silver老师的强化学习 Policy Gradient 讲解课件 ，这种方法也叫 Monte-Carlo Policy Gradient

上图中的 $\log {\pi }_{\theta }(s_t,a_t)$ 是 policy network 输出的概率，$v_t$ 是当前这一局的结果。这是 policy gradient 最基本的更新形式。

但我们前面也分析了：最后的结果好久并不能说明其中每一步都好。我们能不能抛弃回合更新的做法，加快到单步更新呢，Actor-Critic 算法就做了这个调整。

但要采用单步更新，我们就需要为每一步都即时做出评估。Actor-Critic 算法中的 Critic 负责的就是评估这部分工作，而 Actor 则是负责选择出要执行的动作。这就是 Actor-Critic 的思想。Critic 的输出有多种形式，可以采用 $Q$ 值、$V$ 值 或 $TD$ 等。

总结一下Actor-Critic算法核心思想：

在 Actor-Critic 算法中，Critic 是评判模块（多采用深度神经网络方法），它会对动作的好坏评价，然后反馈给 Actor（多采用深度神经网络方法），让 Actor 更新策略。

从具体的训练细节来说，Actor 和 Critic 分别采用不同的目标函数进行更新， 可以参考的代码实现如[这里](https://keras.io/examples/rl/actor_critic_cartpole/）。

3.DDPG算法（Deep Deterministic Policy Gradient）

对于action动作个数是离散和有限的情况，我们前面提到的Policy Gradient梯度策略算法是OK的，但有些情况下输出的值是连续的，比如说「自动驾驶控制的速度」，「机器人控制移动的幅度」，「游戏中调整的角度」等，那梯度策略就不管用了。

在 Deterministic Policy Gradient Algorithms 这篇论文中提出了输出连续动作值的 DPG（Deterministic Policy Gradient），之后论文 Continuous control with deep reinforcement learning 基于 DPG 做了改进，提出了 DDPG（Deep Deterministic Policy Gradient）算法。

DPG算法主要证明了 deterministic policy gradient不仅存在，而且是model-free形式且是action-value function的梯度。因此 policy 不仅仅可以通过概率分布表示，动作空间可以无限大。

DDPG 相对于 DPG 的核心改进是引入了 Deep Learning，采用深度神经网络作为 DPG 中的Policy策略函数 $\mu$ 和 $Q$ 函数的模拟，即 Actor 网络和 Critic 网络；然后使用深度学习的方法来训练上述神经网络。DDPG与DPG的关系类似于 DQN 与 Q-learning 的关系。

DDPG算法中有2个网络：「Actor 网络」与 「Critic 网络」：

• ① 对于状态 $s$，基于Actor网络获取动作action $a$（这里的 $a$ 是一个向量）
• ② 将 $a$ 输入 Critic 网络，得到 $Q$ 值（输出），目标函数就是极大化 $Q$ 值

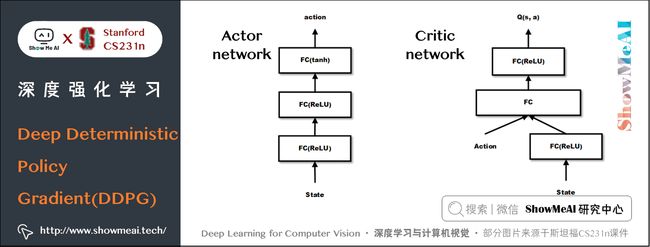
具体的「Actor 网络」和 「Critic 网络」更新有一差异，DDPG论文中算法流程如下图所示：

如上图，Actor 网络和 Critic 网络是分开训练的，但两者的输入输出存在联系，Actor 网络输出的 action 是 Critic 网络的输入，同时 Critic 网络的输出会被用到 Actor 网络进行反向传播。

两个网络的参考示意图如下：Critic 跟之前提到的 DQN 有点类似，但是这里的输入是 state + action，输出是一个 $Q$ 值而不是各个动作的 $Q$ 值。

在DDPG算法中，我们不再用单一的概率值表示某个动作，而是用向量表示某个动作，由于向量空间可以被认为是无限的，因此也能够跟无限的动作空间对应起来。DDPG的代码实现可以参考 这里。

4.A3C算法（Asynchronous Advantage Actor-Critic）

DDPG算法之后，DeepMind对其改造，提出了效果更好的 Asynchronous Advantage Actor-Critic（A3C）算法（论文是 Asynchronous Methods for Deep Reinforcement Learning ）。A3C 算法和DDPG类似，通过深度神经网络拟合 policy function 和 value function的估计。改进点在于：

• ① A3C 中有多个 agent 对网络进行异步更新，这样的做法使得样本间的相关性较低，A3C中也无需采用Experience Replay的机制，且支持在线的训练模式。
• ② A3C 有两个输出，其中一个 Softmax output 作为 policy $\pi (a_t|s_t;\theta )$，而另一个linear output为 value function $V(s_t;{\theta }_v)$ 。
• ③ A3C 中的Policy network 的评估指标采用的是上面比较了多种评估指标的论文中提到的 Advantage Function（即A值) 而不是 DDPG 中单纯的 $Q$ 值。

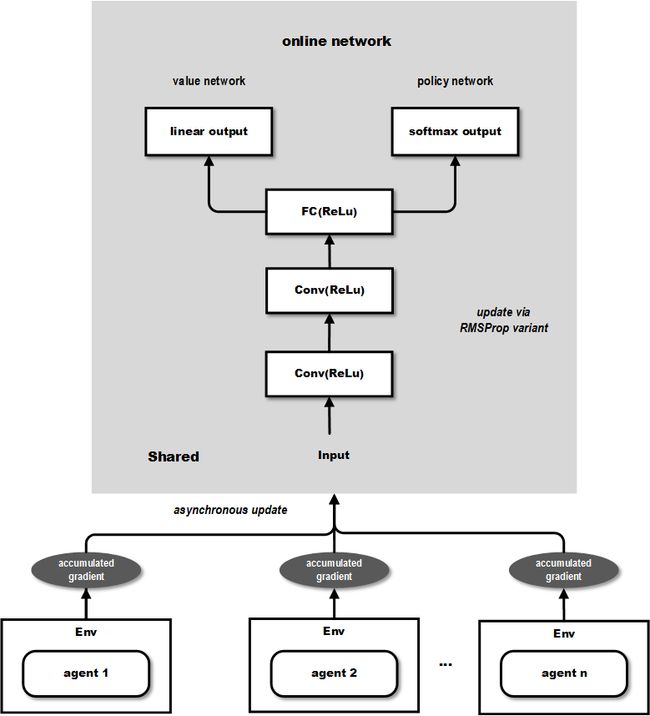
下图（摘自 这篇文章 ）展示了其网络结构：

从上图可以看出输出包含2个部分，value network 的部分可以用来作为连续动作值的输出，而 policy network 可以作为离散动作值的概率输出，因此能够同时解决前面提到的2类问题。

两个网络的更新公式如下：

• Estimate state-value function

$$V(s,\mathbf{v})\approx \mathbb{E}\left[r_{t+1}+\gamma r_{t+2}+\dots \mid s\right]$$

• Q-value estimated by an n -step sample

$$q_t=r_{t+1}+\gamma r_{t+2\cdots }+{\gamma }^{n-1}{r}_{t+n}+{\gamma }^{n}V\left(s_{t+n},\mathbf{v}\right)$$

• Actor is updated towards target

$$\frac{\partial I_u}{\partial \mathbf{u}}=\frac{\partial \log \pi \left(a_t\mid s_t,\mathbf{u}\right)}{\partial \mathbf{u}}\left(q_t-V\left(s_t,\mathbf{v}\right)\right)$$

• Critic is updated to minimise MSE w.r.t. Target

$$I_v={\left(q_t-V\left(s_t,\mathbf{v}\right)\right)}^2$$

A3C 通过创建多个 agent，在多个环境实例中并行且异步的执行和学习，有个潜在的好处是不那么依赖于 GPU 或大型分布式系统，实际上 A3C 可以跑在一个多核 CPU 上，而工程上的设计和优化也是原始paper的一个重点。

A3C的代码实现可以参考这里

5.算法总结

• 我们从最基础的Policy Gradient梯度策略方法开始介绍，最基础的版本是「回合更新」的。
• 引入Critic 后变成了「单步更新」，进而演变为Actor-Critic算法，其中Critic 有多种可选的方法。
• 输出动作为连续值的情形，无法通过输出动作概率分布方式解决，因此提出了 DPG 和 DDPG算法，DDPG 对 DPG 的改进在于引入深度神经网络去拟合 policy function 和 value function。
• 在 DDPG 基础上又提出了效果更好的 A3C算法，这个方法在 DDPG 上引入了多个 agent 对网络进行 异步更新，不仅取得了更好的效果，而且降低了训练的代价。

6.拓展学习

可以点击 B站 查看视频的【双语字幕】版本

【字幕+资料下载】斯坦福CS231n | 面向视觉识别的卷积神经网络 (2017·全16讲)

• 【课程学习指南】斯坦福CS231n | 深度学习与计算机视觉
• 【字幕+资料下载】斯坦福CS231n | 深度学习与计算机视觉 (2017·全16讲)
• 【CS231n进阶课】密歇根EECS498 | 深度学习与计算机视觉
• 【深度学习教程】吴恩达专项课程 · 全套笔记解读
• 【Stanford官网】CS231n: Deep Learning for Computer Vision

7.参考资料

• 强化学习笔记(3)- 从 Policy Gradient 到 A3C
• 深度增强学习之Policy Gradient方法1
• Deep Reinforcement Learning: Pong from Pixels
• 深度增强学习（DRL）漫谈 - 从AC（Actor-Critic）到A3C（Asynchronous Advantage Actor-Critic）
• 深度强化学习（Deep Reinforcement Learning）入门：RL base & DQN-DDPG-A3C introduction

ShowMeAI 斯坦福 CS231n 全套解读

• 深度学习与计算机视觉教程(1) | CV引言与基础 @CS231n
• 深度学习与计算机视觉教程(2) | 图像分类与机器学习基础 @CS231n
• 深度学习与计算机视觉教程(3) | 损失函数与最优化 @CS231n
• 深度学习与计算机视觉教程(4) | 神经网络与反向传播 @CS231n
• 深度学习与计算机视觉教程(5) | 卷积神经网络 @CS231n
• 深度学习与计算机视觉教程(6) | 神经网络训练技巧 (上) @CS231n
• 深度学习与计算机视觉教程(7) | 神经网络训练技巧 (下) @CS231n
• 深度学习与计算机视觉教程(8) | 常见深度学习框架介绍 @CS231n
• 深度学习与计算机视觉教程(9) | 典型CNN架构 (Alexnet, VGG, Googlenet, Restnet等) @CS231n
• 深度学习与计算机视觉教程(10) | 轻量化CNN架构 (SqueezeNet, ShuffleNet, MobileNet等) @CS231n
• 深度学习与计算机视觉教程(11) | 循环神经网络及视觉应用 @CS231n
• 深度学习与计算机视觉教程(12) | 目标检测 (两阶段, R-CNN系列) @CS231n
• 深度学习与计算机视觉教程(13) | 目标检测 (SSD, YOLO系列) @CS231n
• 深度学习与计算机视觉教程(14) | 图像分割 (FCN, SegNet, U-Net, PSPNet, DeepLab, RefineNet) @CS231n
• 深度学习与计算机视觉教程(15) | 视觉模型可视化与可解释性 @CS231n
• 深度学习与计算机视觉教程(16) | 生成模型 (PixelRNN, PixelCNN, VAE, GAN) @CS231n
• 深度学习与计算机视觉教程(17) | 深度强化学习 (马尔可夫决策过程, Q-Learning, DQN) @CS231n
• 深度学习与计算机视觉教程(18) | 深度强化学习 (梯度策略, Actor-Critic, DDPG, A3C) @CS231n

ShowMeAI 系列教程推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读