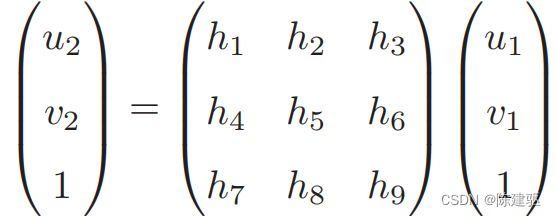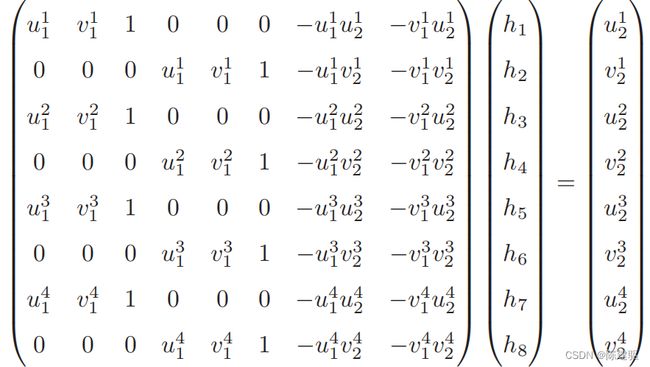对极几何-三角测量-知识点
单目SLAM
对极约束
所谓极线约束就是说同一个点在两幅图像上的映射,已知左图映射点 p 1 \boldsymbol{p}_1 p1 ,那么右图映射点 p 2 \boldsymbol{p}_2 p2 一定在相对于 p 1 \boldsymbol{p}_1 p1 的极线上,这样可以减少待匹配的点数量。(画图解释)
对极约束的推导
3D点的投影:
[ u v 1 ] = 1 Z [ f x 0 c x 0 f y c y 0 0 1 ] [ X Y Z ] ≡ 1 Z K P \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \frac{1}{Z} \begin{bmatrix} f_x && 0 && c_x \\ 0 && f_y && c_y \\ 0 && 0 && 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \equiv \frac{1}{Z} \bold{K} \bold{P} ⎣ ⎡uv1⎦ ⎤=Z1⎣ ⎡fx000fy0cxcy1⎦ ⎤⎣ ⎡XYZ⎦ ⎤≡Z1KP
在第一帧的坐标系下, P P P 的空间位置为 P = [ X , Y , Z ] T \boldsymbol{P}=[X,Y,Z]^T P=[X,Y,Z]T ,两个像素点的位置为 p 1 , p 2 \bold{p}_1,\bold{p}_2 p1,p2 ,深度为 s 1 , s 2 s_1,s_2 s1,s2。根据相机模型,有:
s 1 p 1 = K P s 2 p 2 = K ( R P + t ) s_{1}\mathbf{p}_{1} = \mathbf{K}\mathbf{P} \\ s_{2}\mathbf{p}_{2} = \mathbf{K}\left( \mathbf{R}\mathbf{P} + \mathbf{t} \right) s1p1=KPs2p2=K(RP+t)
K \bold{K} K 为相机内参矩阵, R , t \bold{R},\bold{t} R,t,为第一个坐标系到第二个坐标系的运动。 s 1 p 1 s_1 \bold{p}_1 s1p1和 p 1 \bold{p}_1 p1 成投影关系,它们在齐次坐标的意义下是相等的,称这种相等关系为尺度意义下相等(equal up to a scale),记作:$s \bold{p} \cong \bold{p} $ 。因此上面的投影关系写为:
p 1 ≅ K P p 2 ≅ K ( R P + t ) \mathbf{p}_{1} \cong \mathbf{K}\mathbf{P} \\ \mathbf{p}_{2} \cong \mathbf{K} (\mathbf{RP}+\mathbf{t}) p1≅KPp2≅K(RP+t)
取 x 1 , x 2 \bold{x}_1,\bold{x}_2 x1,x2 是P点投影到归一化平面上的坐标,有:
p 1 = K x 1 , p 2 = K x 2 ⇒ x 1 = K − 1 p 1 , x 2 = K − 1 p 2 \left. \bold{p}_{1} = \bold{K}\bold{x}_{1},\bold{p}_{2} = \bold{K}\bold{x}_{2} \\ \Rightarrow \bold{x}_{1} = \bold{K}^{- 1}\bold{p}_{1},\bold{x}_{2} = \bold{K}^{- 1}\bold{p}_{2} \right. p1=Kx1,p2=Kx2⇒x1=K−1p1,x2=K−1p2
将 x 1 , x 2 \bold{x}_1,\bold{x}_2 x1,x2 代入上式,得:
p 1 ≅ K P , p 2 ≅ K ( R P + t ) ⇒ K x 1 ≅ K P , K x 2 ≅ K ( R P + t ) ⇒ x 1 ≅ P , x 2 ≅ R P + t ⇒ x 2 ≅ R x 1 + t \left. \bold{p}_{1} \cong \bold{KP},\bold{p}_{2} \cong \bold{K}(\bold{RP} + \bold{t}) \\ \Rightarrow \bold{K}\bold{x}_{1} \cong \bold{KP},\bold{K} \bold{x}_{2} \cong \bold{K}(\bold{RP} + \bold{t}) \\ \Rightarrow \bold{x}_{1} \cong \bold{P},\bold{x}_{2} \cong \bold{RP} + \bold{t} \\ \Rightarrow \bold{x}_{2} \cong \bold{R} \bold{x}_{1} + \bold{t} \right. p1≅KP,p2≅K(RP+t)⇒Kx1≅KP,Kx2≅K(RP+t)⇒x1≅P,x2≅RP+t⇒x2≅Rx1+t
两边同时与 t \bold{t} t 做外积:
t ∧ x 2 ≅ t ∧ R x 1 \bold{t}^{\land}\bold{x}_{2} \cong \bold{t}^{\land} \bold{R} \bold{x}_{1} t∧x2≅t∧Rx1
然后两侧同时左乘 x 2 T \bold{x}_2^T x2T :
x 2 T t ∧ x 2 ≅ x 2 T t ∧ R x 1 \bold{x}_{2}^{T} \bold{t}^{\land} \bold{x}_{2} \cong \bold{x}_{2}^{T} \bold{t}^{\land} \bold{R} \bold{x}_{1} x2Tt∧x2≅x2Tt∧Rx1
t ∧ x 2 \bold{t}^{\land} \bold{x}_2 t∧x2 是一个与 t \bold{t} t 和 x 2 \boldsymbol{x}_2 x2 都垂直的向量,把它再和 x 2 \boldsymbol{x}_2 x2 做内积时,将得到0。因此可以省略掉尺度不变性,得:
x 2 T t ∧ R x 1 = 0 \bold{x}_{2}^{T} \bold{t}^{\land} \bold{R} \bold{x}_{1} = 0 x2Tt∧Rx1=0
重新代入 p 1 , p 2 \bold{p}_1,\bold{p}_2 p1,p2 , 得:
p 2 T K − T t ∧ R K − 1 p 1 = 0 \bold{p}_{2}^{{T}}\bold{K}^{-{T}} \bold{t}^{\land} \bold{RK}^{- 1} \bold{p}_{1} = 0 p2TK−Tt∧RK−1p1=0
对极约束
上面两个公式都称为对极约束,几何意义是 O 1 , P , O 2 O_1,P,O_2 O1,P,O2 三者共面。对极约束中同时包含了平移和旋转。记中间部分为基础矩阵 F \bold{F} F (Fundamental Matrix)和 本质矩阵 E \bold{E} E (Essential Matrix),对极约束为:
E = t ∧ R F = K − T E K − 1 = K − T t ∧ R K − 1 x 2 T E x 1 = p 2 T F p 1 = 0 \mathbf{E} = \mathbf{t}^{\land}\mathbf{R} \\ \mathbf{F} = \mathbf{K}^{- {T}}\mathbf{E}\mathbf{K}^{- 1} = \mathbf{K}^{- {T}}\mathbf{t}^{\land}\mathbf{R}\mathbf{K}^{- 1} \\ \mathbf{x}_{2}^{T}\mathbf{E}\mathbf{x}_{1} = \mathbf{p}_{2}^{T}\mathbf{F}\mathbf{p}_{1} = 0 E=t∧RF=K−TEK−1=K−Tt∧RK−1x2TEx1=p2TFp1=0
于是,相机位姿估计问题变为以下两步:
-
根据配对点的像素位置求出 E \bold{E} E 或者 F \bold{F} F 。
-
根据 E \bold{E} E 或 F \bold{F} F 求出 R , t \bold{R,t} R,t 。
极线约束的好处:从上面的描述我们可以看到,我们在做特征点匹配时,左图成像点 p 1 p_1 p1 的待匹配点 p 2 p_2 p2 一定在相对于 p 1 p_1 p1 的极线上,那么我们在做搜索时就可以在极线附近(考虑实际可能 会有一点误差)进行搜索,相对暴力匹配极大减少待匹配的点的数量。
https://www.cnblogs.com/CV-life/p/11159820.html
极线约束也叫对极约束。这个约束的意思就是说,假设相机在不同位置拍摄了两幅图像,如果一个空间点P在两幅图上分别有两个成像点,已知左图成像点为p1,那么右图成像点p2一定在相对于p1的极线上。
极线约束的好处:从上面的描述我们可以看到,我们在做特征点匹配时,左图成像点p1的待匹配点p2一定在相对于p1的极线上,那么我们在做搜索时就可以在极线附近(考虑实际可能 会有一点误差)进行搜索,相对暴力匹配极大减少待匹配的点的数量。
极线约束可以简洁的给出匹配点的空间位置关系,使得相机位姿估计问题变的简单。
本质矩阵、基础矩阵、单应矩阵
本质矩阵E和基础矩阵F
本质矩阵和基础矩阵是对极约束的表示形式,对极约束中同时包含了平移和旋转。记 K K K 为相机内参矩阵, R , t \bold{R},\bold{t} R,t 为坐标系 O 1 O_1 O1 到坐标系 O 2 O_2 O2 的运动。
本质矩阵 E (Essential Matrix):
E = t ∧ R \bold{E} = \bold{t}^{\land} \bold{R} E=t∧R
基础矩阵 F (Fundamental Matrix):
F = K − T E K − 1 \bold{F} = \bold{K} ^{-T} \bold{E} \bold{K}^{-1} F=K−TEK−1
对极约束为:
x 2 T E x 1 = p 2 T F p 1 = 0 \boldsymbol{x}_2^T \bold{E} \boldsymbol{x}_1 = \boldsymbol{p}_2^T \bold{F} \boldsymbol{p}_1 = 0 x2TEx1=p2TFp1=0
其中 p 1 , p 2 \boldsymbol{p}_1,\boldsymbol{p}_2 p1,p2 是像素坐标, x 1 , x 2 \boldsymbol{x}_1,\boldsymbol{x}_2 x1,x2 是归一化坐标。
单应矩阵H
单应矩阵:描述了两个平面之间的映射关系。若场景中的特征点都落在同一平面上(比如墙、地面等),则可以通过单应性来进行运动估计。这种情况在无人机携带的俯视相机或扫地机携带的顶视相机中比较常见。
单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系。考虑在图像 I 1 I_1 I1 和 I 2 I_2 I2 有一对匹配好的特征点 p 1 p_1 p1 和 p 2 p_2 p2 。这些特征点落在平面 P \bold{P} P 上,设这个平面满足方程: n T P + d = 0 \boldsymbol{n}^T \bold{P} + \boldsymbol{d} = 0 nTP+d=0 ,整理得:
− n T P d = 1 -\frac{\mathbf{n}^{T}\mathbf{P}}{\mathbf{d}} = 1 −dnTP=1
前面说过的尺度意义下相等,得:
p 2 = K ( R P + t ) = K ( R P + t ⋅ ( − n T P d ) ) = K ( R − t n T d ) P = K ( R − t n T d ) K − 1 p 1 \mathbf{p}_{2} = \mathbf{K}\left( {\mathbf{R}\mathbf{P} + \mathbf{t}} \right) \\ = \mathbf{K}\left( {\mathbf{R}\mathbf{P} + \mathbf{t} \cdot \left( {- \frac{\mathbf{n}^{T}\mathbf{P}}{d}} \right)} \right) \\ = \mathbf{K}\left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{d}} \right)\mathbf{P} \\ = \mathbf{K}\left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{d}} \right)\mathbf{K}^{- 1}\mathbf{p}_{1} p2=K(RP+t)=K(RP+t⋅(−dnTP))=K(R−dtnT)P=K(R−dtnT)K−1p1
得到了一个直接描述图像坐标 p 1 p_1 p1 和 p 2 p_2 p2 之间的变换,把中间这部分记为 单应矩阵 H \bold{H} H :
H = ( R − t n T d ) \mathbf{H} = \left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{\mathbf{d}}} \right) H=(R−dtnT)
于是:
p 2 = H p 2 p_2 = \mathbf{H} p_2 p2=Hp2
它的定义与旋转、平移及平面的参数有关。
E、F、H的自由度和秩
视觉SLAM中,本质矩阵、基础矩阵、单应性矩阵自由度和秩分析
本质矩阵 E \bold{E} E :由于平移和旋转各有 3 个自由度,故 t ∧ R \bold{t}^{\land}\bold{R} t∧R 共有 6 个自由度。但由于尺度等价性,故 E \bold{E} E 实际上有 5 个自由度,秩为2。
自由度:
旋转和平移一共6个自由度。由于对极约束的原因,本质矩阵是具有尺度等价性的,所以自由度减1。所以,本质矩阵的自由度为5。
PS:旋转矩阵虽然9个参数,但不是任意数都可以,得满足矩阵为单位(去掉3个自由度)正交(去掉2个自由度)阵,行列式为正1(去掉1个自由度)的性质,所以,这些约束导致自由度减少,虽然是9个数但是表达3个自由度。
秩:
旋转矩阵秩为3,是可逆矩阵。平移的反对称矩阵秩为2。所以本质矩阵的秩为2。
基础矩阵 F \bold{F} F : F \bold{F} F 矩阵的参数数量是3x3=9,但是因为尺度等价性,因此自由度减一 ;又因为 F \bold{F} F满足 det ( F ) = 0 \text{det}(\bold{F})=0 det(F)=0 ,自由度再减一 。故 矩阵有7个自由度,秩为2。由于每对特征只提供了一个约束,因此最少需要7对特征来求解。
自由度:
基础矩阵也是一个3x3的矩阵。其仍然受对极约束的影响,具有尺度等价性。基础矩阵的行列式为0。
最后得到,基础矩阵的自由度为7。
秩:
相机内参矩阵秩为3,旋转矩阵秩为3。平移反对称矩阵秩为2。最后,同样由性质2得出,基础矩阵的秩为2。
单应矩阵 H \bold{H} H :自由度为8。使用DLT求解时,每对特征提供两个约束,因此至少需要4对点求解。
自由度:
单应性矩阵也是一个3x3的矩阵。其具有尺度等价性。最后得到,基础矩阵的自由度为8。
秩:
因为单应性矩阵是可逆矩阵,所以他的秩为3。
基础矩阵的性质
基础矩阵F的求解
基础矩阵最少只需要7对点(7个自由度,每对点提供一个约束)即可计算出来。根据基础矩阵的对极约束,同样可以采用8点法来求解基础矩阵 F \mathbf{F} F :
p 2 T F p 1 = 0 \mathbf{p}_{2}^{T}\mathbf{F}\mathbf{p}_{1} = 0 p2TFp1=0
假设一对匹配点,其像素坐标为 p 1 = [ u 1 , v 1 , 1 ] T , p 2 = [ u 2 , v 2 , 1 ] T \mathbf{p}_{1} = \left\lbrack {u_{1},v_{1},1} \right\rbrack^{T},\mathbf{p}_{2} = \left\lbrack {u_{2},v_{2},1} \right\rbrack^{T} p1=[u1,v1,1]T,p2=[u2,v2,1]T,根据对极约束得:
p 2 T F p 1 = [ u 2 v 2 1 ] [ f 1 f 2 f 3 f 4 f 5 f 6 f 7 f 8 f 9 ] [ u 1 v 1 1 ] = 0 \mathbf{p}_{2}^{T}\mathbf{F}\mathbf{p}_{1} = \begin{bmatrix} u_{2} & v_{2} & 1 \\ \end{bmatrix}\begin{bmatrix} f_{1} & f_{2} & f_{3} \\ f_{4} & f_{5} & f_{6} \\ f_{7} & f_{8} & f_{9} \\ \end{bmatrix}\begin{bmatrix} u_{1} \\ v_{1} \\ 1 \\ \end{bmatrix} = 0 p2TFp1=[u2v21]⎣ ⎡f1f4f7f2f5f8f3f6f9⎦ ⎤⎣ ⎡u1v11⎦ ⎤=0
将本质矩阵 F \mathbf{F} F 展开, f = [ f 1 , f 2 , f 3 , f 4 , f 5 , f 6 , f 7 , f 8 , f 9 ] T \mathbf{f} = \left\lbrack {f_{1},f_{2},f_{3},f_{4},f_{5},f_{6},f_{7},f_{8},f_{9}} \right\rbrack^{T} f=[f1,f2,f3,f4,f5,f6,f7,f8,f9]T ,则对极约束写成 F \mathbf{F} F 有关的形式。SLAM14讲书上推得到:
[ u 1 u 2 , v 1 u 2 , u 2 , u 1 v 2 , v 1 v 2 , v 2 , u 1 , v 1 , 1 ] ∗ f = 0 \left\lbrack u_{1}u_{2},v_{1}u_{2},u_{2},u_{1}v_{2},v_{1}v_{2},v_{2},u_{1},v_{1},1 \right\rbrack*\mathbf{f} = 0 [u1u2,v1u2,u2,u1v2,v1v2,v2,u1,v1,1]∗f=0
将8对匹配点放在同一方程组里,得:
如果 8 对匹配点组成的矩阵满足秩为 8 的条件,那么 F \mathbf{F} F 的各元素就可由上述方程解得。上式是 Ax=0 的问题,使用SVD求最小二乘解即可得到 F \mathbf{F} F 矩阵。
将 F \mathbf{F} F 矩阵恢复为 t , R \mathbf{t,R} t,R 。首先使用内参矩阵 将 F \mathbf{F} F 矩阵转换为 E \mathbf{E} E 矩阵,再将 E \mathbf{E} E 分解为 t , R \mathbf{t,R} t,R 。
本质矩阵E的分解为R,t
反对称矩阵的特征值形式
于 t ∧ \bold{t}^{\land} t∧ 的特征值为 λ 1 = 0 , λ 2 , 3 = i ∥ t ∥ 2 \lambda_{1} = 0,\lambda_{2,3} = i\left\| \mathbf{t} \right\|_{2} λ1=0,λ2,3=i∥t∥2 ,其中 ∥ t ∥ 2 \left\| \mathbf{t} \right\|_{2} ∥t∥2 表示 t \bold{t} t 的模。
推导:TODO
E的分解
得到 E \mathbf{E} E 之后,因为有 E = t ∧ R \mathbf{E} = \bold{t} ^{\land} \bold{R} E=t∧R ,可以通过SVD分解获得 t , R \mathbf{t,R} t,R 。
根据 E \mathbf{E} E 和 R \mathbf{R} R 的性质,有:
E E T = t ∧ R ( t ∧ R ) T = t ∧ R R T t ∧ T = t ∧ t ∧ T = t ∧ ( − t ∧ ) = − t ∧ 2 \mathbf{E}\mathbf{E}^{T} = \mathbf{t}^{\land}\mathbf{R}\left( {\mathbf{t}^{\land}\mathbf{R}} \right)^{T} = \mathbf{t}^{\land}\mathbf{R}\mathbf{R}^{T}{\mathbf{t}^{\land}}^{T} = \mathbf{t}^{\land}{\mathbf{t}^{\land}}^{T} = \mathbf{t}^{\land}\left( {- \mathbf{t}^{\land}} \right) = - {\mathbf{t}^{\land}}^{2} EET=t∧R(t∧R)T=t∧RRTt∧T=t∧t∧T=t∧(−t∧)=−t∧2
由于 t ∧ \bold{t}^{\land} t∧ 的特征值为 λ 1 = 0 , λ 2 , 3 = i ∥ t ∥ 2 \lambda_{1} = 0,\lambda_{2,3} = i\left\| \mathbf{t} \right\|_{2} λ1=0,λ2,3=i∥t∥2 ,其中 ∥ t ∥ 2 \left\| \mathbf{t} \right\|_{2} ∥t∥2 表示 t \bold{t} t 的模。所以 E E T \mathbf{E}\mathbf{E}^{T} EET 的特征值为 − λ 2 -\lambda^2 −λ2 ,也就是 λ 1 = 0 , λ 2 , 3 = ∥ t ∥ 2 2 \lambda_{1} = 0,\lambda_{2,3} = \left\| \mathbf{t} \right\|_{2}^{2} λ1=0,λ2,3=∥t∥22 。所以 E \mathbf{E} E 的奇异值就等于平移向量的二范数或者模长。
假设有SVD分解:
E = U Σ V T = U [ a 0 0 0 a 0 0 0 0 ] V T = t ∧ R , a > 0 \mathbf{E}~ = ~\mathbf{U}\mathbf{\Sigma}\mathbf{V}^{T} = \mathbf{U}\begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\mathbf{V}^{T} = \mathbf{t}^{\land}\mathbf{R},\mathbf{~}a > 0 E = UΣVT=U⎣ ⎡a000a0000⎦ ⎤VT=t∧R, a>0
则 α = ∥ t ∥ 2 \alpha = \Vert \bold{t} \Vert_2 α=∥t∥2 。 U \mathbf{U} U 和 V \mathbf{V} V 都是酉矩阵,如果复矩阵 U \mathbf{U} U 满足 U H U = U U T = I \mathbf{U}^{H}\mathbf{U} = \mathbf{U}\mathbf{U}^{T} = \mathbf{I} UHU=UUT=I ,或 U H = U ˉ T \mathbf{U}^{H} = \bold{\bar{U}}^T UH=UˉT ,则称 为酉矩阵 U \mathbf{U} U (复正交矩阵)。
又因为:
Σ = [ a 0 0 0 a 0 0 0 0 ] = [ 0 a 0 − a 0 0 0 0 0 ] [ 0 − 1 0 1 0 0 0 0 1 ] \mathbf{\Sigma} = \begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} = \begin{bmatrix} 0 & a & 0 \\ {- a} & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} 0 & {- 1} & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} Σ=⎣ ⎡a000a0000⎦ ⎤=⎣ ⎡0−a0a00000⎦ ⎤⎣ ⎡010−100001⎦ ⎤
则:
E = U [ a 0 0 0 a 0 0 0 0 ] V T = U [ 0 a 0 − a 0 0 0 0 0 ] [ 0 − 1 0 1 0 0 0 0 1 ] V T = U [ 0 a 0 − a 0 0 0 0 0 ] U T U [ 0 − 1 0 1 0 0 0 0 1 ] V T = t ∧ R \mathbf{E}~ = ~\mathbf{U}\begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\mathbf{V}^{T} = \mathbf{U}\begin{bmatrix} 0 & a & 0 \\ {- a} & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} 0 & {- 1} & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\mathbf{V}^{T} \\ = \mathbf{U}\begin{bmatrix} 0 & a & 0 \\ {- a} & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\mathbf{U}^{T}\mathbf{U}\begin{bmatrix} 0 & {- 1} & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\mathbf{V}^{T} = \mathbf{t}^{\land}\mathbf{R} E = U⎣ ⎡a000a0000⎦ ⎤VT=U⎣ ⎡0−a0a00000⎦ ⎤⎣ ⎡010−100001⎦ ⎤VT=U⎣ ⎡0−a0a00000⎦ ⎤UTU⎣ ⎡010−100001⎦ ⎤VT=t∧R
得平移:
t ∧ = U [ 0 a 0 − a 0 0 0 0 0 ] U T = ( U [ 0 0 a ] ) ∧ t = U [ 0 0 a ] = [ U 0 U 1 U 2 ] [ 0 0 a ] = U 2 a \mathbf{t}^{\land} = \mathbf{U}\begin{bmatrix} 0 & a & 0 \\ {- a} & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\mathbf{U}^{T} = \left( {\mathbf{U}\begin{bmatrix} 0 \\ 0 \\ a \\ \end{bmatrix}} \right)^{\land} \\ \mathbf{t} = \mathbf{U}\begin{bmatrix} 0 \\ 0 \\ a \\ \end{bmatrix} = \begin{bmatrix} \mathbf{U}_{0} & \mathbf{U}_{1} & \mathbf{U}_{2} \\ \end{bmatrix}\begin{bmatrix} 0 \\ 0 \\ a \\ \end{bmatrix} = \mathbf{U}_{2}a t∧=U⎣ ⎡0−a0a00000⎦ ⎤UT=⎝ ⎛U⎣ ⎡00a⎦ ⎤⎠ ⎞∧t=U⎣ ⎡00a⎦ ⎤=[U0U1U2]⎣ ⎡00a⎦ ⎤=U2a
得旋转:
R = U [ 0 − 1 0 1 0 0 0 0 1 ] V T ≡ U W V T \mathbf{R} = \mathbf{U}\begin{bmatrix} 0 & {- 1} & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\mathbf{V}^{T} \equiv \mathbf{U}\mathbf{W}\mathbf{V}^{T} R=U⎣ ⎡010−100001⎦ ⎤VT≡UWVT
此外, 还有另一种分解:
Σ = [ a 0 0 0 a 0 0 0 0 ] = [ 0 − a 0 a 0 0 0 0 0 ] [ 0 1 0 − 1 0 0 0 0 1 ] \mathbf{\Sigma} = \begin{bmatrix} a & 0 & 0 \\ 0 & a & 0 \\ 0 & 0 & 0 \\ \end{bmatrix} = \begin{bmatrix} 0 & {- a} & 0 \\ a & 0 & 0 \\ 0 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} 0 & 1 & 0 \\ {- 1} & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} Σ=⎣ ⎡a000a0000⎦ ⎤=⎣ ⎡0a0−a00000⎦ ⎤⎣ ⎡0−10100001⎦ ⎤
此时,得:
t = U [ 0 0 − a ] = [ U 0 U 1 U 2 ] [ 0 0 − a ] = − U 2 a R = U [ 0 1 0 − 1 0 0 0 0 1 ] V T ≡ U W T V T \mathbf{t} = \mathbf{U}\begin{bmatrix} 0 \\ 0 \\ {- a} \\ \end{bmatrix} = \begin{bmatrix} \mathbf{U}_{0} & \mathbf{U}_{1} & \mathbf{U}_{2} \\ \end{bmatrix}\begin{bmatrix} 0 \\ 0 \\ {- a} \\ \end{bmatrix} = - \mathbf{U}_{2}a \\ \mathbf{R} = \mathbf{U}\begin{bmatrix} 0 & 1 & 0 \\ {- 1} & 0 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}\mathbf{V}^{T} \equiv \mathbf{U}\mathbf{W}^{T}\mathbf{V}^{T} t=U⎣ ⎡00−a⎦ ⎤=[U0U1U2]⎣ ⎡00−a⎦ ⎤=−U2aR=U⎣ ⎡0−10100001⎦ ⎤VT≡UWTVT
因此, t \bold{t} t 和 R \bold{R} R 都有两种情况:
- t 2 = − t 1 \mathbf{t}_{2} = - \mathbf{t}_{1} t2=−t1
- R 2 \bold{R}_2 R2 是 R 1 \bold{R}_1 R1 绕( t \bold{t} t 平移向量)旋转 π \pi π 弧度。
因此,在SVD分解中,一个 存在两个可能的 t \bold{t} t 和 R \bold{R} R 与之对应:
t 1 ∧ = U R z ( π 2 ) Σ U T , R 1 = U R Z T ( π 2 ) V T t 1 ∧ = U R z ( − π 2 ) Σ U T , R 1 = U R Z T ( − π 2 ) V T {\mathbf{t}_{1}}^{\land} = \mathbf{U}\mathbf{R}_{z}\left( \frac{\pi}{2} \right)\mathbf{\Sigma}\mathbf{U}^{T},\mathbf{~}\mathbf{~}\mathbf{R}_{1} = \mathbf{U}\mathbf{R}_{Z}^{T}\left( \frac{\pi}{2} \right)\mathbf{V}^{T} \\ {\mathbf{t}_{1}}^{\land} = \mathbf{U}\mathbf{R}_{z}\left( {- \frac{\pi}{2}} \right)\mathbf{\Sigma}\mathbf{U}^{T},\mathbf{~}\mathbf{~}\mathbf{R}_{1} = \mathbf{U}\mathbf{R}_{Z}^{T}\left( {- \frac{\pi}{2}} \right)\mathbf{V}^{T} t1∧=URz(2π)ΣUT, R1=URZT(2π)VTt1∧=URz(−2π)ΣUT, R1=URZT(−2π)VT
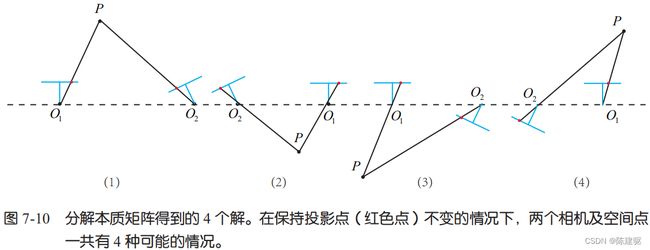
R Z ( π / 2 ) \bold{R}_Z (\pi / 2) RZ(π/2) 表示沿 Z 轴旋转 90◦ 得到的旋转矩阵。由于 − E -\bold{E} −E 和 E \bold{E} E 等价,所以对任意一个 t \bold{t} t 取负号,也会得到同样的结果。因此,从 E \bold{E} E 分解到 t , R \mathbf{t,R} t,R 时,一共存在 4 个可能的解。示意图:
如上图所示,只有第一种解中 P 在两个相机中都具有正的深度。因此,只要把任意一点代入 4 种解中,检测该点在两个相机下的深度,就可以确定哪个解是正确的了。
根据线性方程解出的 E \bold{E} E ,可能不满足 E \bold{E} E 的内在性质——它的奇异值不一定为 σ , σ , 0 \sigma,\sigma,0 σ,σ,0的形式。这时,我们会刻意地把 Σ \bold{\Sigma} Σ 矩阵调整成上面的样子。通常的做法是,对八点法求得的 E \bold{E} E 进行 SVD 分解后,会得到奇异值矩阵 Σ = d i a g ( σ 1 , σ 2 , σ 3 ) \mathbf{\Sigma}~ = ~diag\left( \sigma_{1},~\sigma_{2},~\sigma_{3} \right) Σ = diag(σ1, σ2, σ3) ,不妨设 σ 1 ⩾ σ 2 ⩾ σ 3 \sigma_{1}~ \geqslant ~\sigma_{2}~ \geqslant ~\sigma_{3} σ1 ⩾ σ2 ⩾ σ3 。取:
E = U d i a g ( σ 1 + σ 2 2 , σ 1 + σ 2 2 , 0 ) V T \mathbf{E}~ = \mathbf{U}~diag\left( \frac{\sigma_{1} + \sigma_{2}}{2},~\frac{\sigma_{1} + \sigma_{2}}{2},~0 \right)\mathbf{V}^{T} E =U diag(2σ1+σ2, 2σ1+σ2, 0)VT
这相当于是把求出来的矩阵投影到了 E \bold{E} E 所在的流形上。当然,更简单的做法是将奇异值矩阵取成 d i a g ( 1 , 1 , 0 ) diag(1,1,0) diag(1,1,0) ,因为 E \bold{E} E 具有尺度等价性,所以这样做也是合理的。
由于 E \bold{E} E 本身具有尺度等价性,它分解得到的 t , R \mathbf{t,R} t,R 也有一个尺度等价性。而 R ∈ S O ( 3 ) \bold{R} \in SO(3) R∈SO(3) 自身具有约束,所以我们认为 t \bold{t} t 具有一个尺度。换言之,在分解过程中,对 t \bold{t} t 乘以任意非零常数,分解都是成立的。因此,我们通常把 t \bold{t} t 进行归一化,让它的长度等于 1。
代码实现
下面的代码,将E分解为4种解
/**
* @brief 分解Essential矩阵得到R,t
* 分解E矩阵将得到4组解,这4组解分别为[R1,t],[R1,-t],[R2,t],[R2,-t]
* 参考:Multiple View Geometry in Computer Vision - Result 9.19 p259
* @param[in] E 本质矩阵
* @param[in & out] R1 旋转矩阵1
* @param[in & out] R2 旋转矩阵2
* @param[in & out] t 平移向量,另外一个取相反数
*/
void Initializer::DecomposeE(const cv::Mat &E, cv::Mat &R1, cv::Mat &R2, cv::Mat &t)
{
// 对本质矩阵进行奇异值分解
//准备存储对本质矩阵进行奇异值分解的结果
cv::Mat u,w,vt;
//对本质矩阵进行奇异值分解
cv::SVD::compute(E,w,u,vt);
// 左奇异值矩阵U的最后一列就是t,对其进行归一化
u.col(2).copyTo(t);
t=t/cv::norm(t);
// 构造一个绕Z轴旋转pi/2的旋转矩阵W,按照下式组合得到旋转矩阵 R1 = u*W*vt
//计算完成后要检查一下旋转矩阵行列式的数值,使其满足行列式为1的约束
cv::Mat W(3,3,CV_32F,cv::Scalar(0));
W.at(0,1)=-1;
W.at(1,0)=1;
W.at(2,2)=1;
//计算
R1 = u*W*vt;
//旋转矩阵有行列式为+1的约束,所以如果算出来为负值,需要取反
if(cv::determinant(R1)<0)
R1=-R1;
// 同理将矩阵W取转置来按照相同的公式计算旋转矩阵R2 = u*W.t()*vt
R2 = u*W.t()*vt;
//旋转矩阵有行列式为1的约束
if(cv::determinant(R2)<0)
R2=-R2;
}
单应矩阵H的求解
单应矩阵 H \bold{H} H 也是一个 3 × 3 3 \times 3 3×3 的矩阵,求解时的思路也和 F \bold{F} F 类似,同样可以先根据匹配点计算 H \bold{H} H ,然后将它分解以计算旋转和平移。把上式展开,得:
这里的等号是在非零因子下成立的。我们在实际处理中通常乘以一个非零因子使得 (在它取非零值时)。然后根据第 3 行,去掉这个非零因子,即:
{ u 2 = h 1 u 1 + h 2 v 1 + h 3 v 2 = h 4 u 1 + h 5 v 1 + h 6 1 = h 7 u 1 + h 8 v 1 + h 9 ⇒ { u 2 = h 1 u 1 + h 2 v 1 + h 3 h 7 u 1 + h 8 v 1 + h 9 v 2 = h 4 u 1 + h 5 v 1 + h 6 h 7 u 1 + h 8 v 1 + h 9 \left. \left\{ \begin{matrix} {u_{2} = h_{1}u_{1} + h_{2}v_{1} + h_{3}} \\ {v_{2} = h_{4}u_{1} + h_{5}v_{1} + h_{6}} \\ {1 = h_{7}u_{1} + h_{8}v_{1} + h_{9}} \\ \end{matrix} \right. \\ \Rightarrow\left\{ \begin{matrix} {u_{2} = \frac{h_{1}u_{1} + h_{2}v_{1} + h_{3}}{h_{7}u_{1} + h_{8}v_{1} + h_{9}}} \\ {v_{2} = \frac{h_{4}u_{1} + h_{5}v_{1} + h_{6}}{h_{7}u_{1} + h_{8}v_{1} + h_{9}}} \\ \end{matrix} \right. \right. ⎩ ⎨ ⎧u2=h1u1+h2v1+h3v2=h4u1+h5v1+h61=h7u1+h8v1+h9⇒{u2=h7u1+h8v1+h9h1u1+h2v1+h3v2=h7u1+h8v1+h9h4u1+h5v1+h6
整理得:
h 1 u 1 + h 2 v 1 + h 3 − h 7 u 1 u 2 − h 8 v 1 u 2 = u 2 h 4 u 1 + h 5 v 1 + h 6 − h 7 u 1 v 2 − h 8 v 1 v 2 = v 2 h_1 u_1 + h_2 v_1 + h_3 - h_7 u_1 u_2 - h_8 v_1 u_2 = u_2 \\ h_4 u_1 + h_5 v_1 + h_6 - h_7 u_1 v_2 - h_8 v_1 v_2 = v_2 h1u1+h2v1+h3−h7u1u2−h8v1u2=u2h4u1+h5v1+h6−h7u1v2−h8v1v2=v2
这样一组匹配点对就可以构造出两项约束(事实上有三个约束,但是因为线性相关,只取前两个),于是自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出(注意,这些特征点不能有三点共线的情况),即求解以下的线性方程组(当 h 9 = 0 h_9 =0 h9=0 时,右侧为零):
A x = b \bold{A} \bold{x} = \bold{b} Ax=b
其中 x \bold{x} x 是H矩阵的展开. 这种做法把 H 矩阵看成了向量,通过解该向量的线性方程来恢复H,又称直接线性变换法(Direct Linear Transform**,DLT)**。
当A 超定时,用SVD求解:
// 定义输出变量,u是左边的正交矩阵U, w为奇异矩阵,vt中的t表示是右正交矩阵V的转置
cv::Mat u,w,vt;
//使用opencv提供的进行奇异值分解的函数
cv::SVDecomp(A, //输入,待进行奇异值分解的矩阵
w, //输出,奇异值矩阵
u, //输出,矩阵U
vt, //输出,矩阵V^T
cv::SVD::MODIFY_A | //输入,MODIFY_A是指允许计算函数可以修改待分解的矩阵,官方文档上说这样可以加快计算速度、节省内存
cv::SVD::FULL_UV); //FULL_UV=把U和VT补充成单位正交方阵
// 返回最小奇异值所对应的右奇异向量
// 注意前面说的是右奇异值矩阵的最后一列,但是在这里因为是vt,转置后了,所以是行;由于A有9列数据,故最后一列的下标为8
return vt.row(8).reshape(0,3); //将一个1x9的向量转换为一个3x3的矩阵
单应矩阵H分解为R,t
与本质矩阵相似,求出单应矩阵以后需要对其进行分解,才可以得到相应的旋转矩阵 R 和平移向量 t。分解的方法包括数值法与解析法。
与本质矩阵的分解类似,单应矩阵的分解同样会返回 4 组旋转矩阵与平移向量,并且同时可以计算出它们分别对应的场景点所在平面的法向量。如果已知成像的地图点的深度全为正值(即在相机前方),则又可以排除两组解。最后仅剩两组解,这时需要通过更多的先验信息进行判断。通常我们可以通过假设已知场景平面的法向量来解决,如场景平面与相机平面平行,那么法向量 n \boldsymbol{n} n 的理论值为 1 T \bold{1}^T 1T 。
具体过程:
TODO
手撕代码: DLT求解H矩阵
来自OBR-SLAM
/**
* @brief 用DLT方法求解单应矩阵H
* 这里最少用4对点就能够求出来,不过这里为了统一还是使用了8对点求最小二乘解
*
* @param[in] vP1 参考帧中归一化后的特征点
* @param[in] vP2 当前帧中归一化后的特征点
* @return cv::Mat 计算的单应矩阵H
*/
cv::Mat Initializer::ComputeH21(
const vector &vP1, //归一化后的点, in reference frame
const vector &vP2) //归一化后的点, in current frame
{
// 基本原理:见附件推导过程:
// |x'| | h1 h2 h3 ||x|
// |y'| = a | h4 h5 h6 ||y| 简写: x' = a H x, a为一个尺度因子
// |1 | | h7 h8 h9 ||1|
// 使用DLT(direct linear tranform)求解该模型
// x' = a H x
// ---> (x') 叉乘 (H x) = 0 (因为方向相同) (取前两行就可以推导出下面的了)
// ---> Ah = 0
// A = | 0 0 0 -x -y -1 xy' yy' y'| h = | h1 h2 h3 h4 h5 h6 h7 h8 h9 |
// |-x -y -1 0 0 0 xx' yx' x'|
// 通过SVD求解Ah = 0,A^T*A最小特征值对应的特征向量即为解
// 其实也就是右奇异值矩阵的最后一列
//获取参与计算的特征点的数目
const int N = vP1.size();
// 构造用于计算的矩阵 A
cv::Mat A(2*N, 9 , CV_32F); //每一个点的数据对应两行
// 构造矩阵A,将每个特征点添加到矩阵A中的元素
for(int i=0; i(2*i,0) = 0.0; A.at(2*i,1) = 0.0;A.at(2*i,2) = 0.0; A.at(2*i,3) = -u1; A.at(2*i,4) = -v1;
A.at(2*i,5) = -1; A.at(2*i,6) = v2*u1;A.at(2*i,7) = v2*v1; A.at(2*i,8) = v2;
//生成这个点的第二行
A.at(2*i+1,0) = u1;A.at(2*i+1,1) = v1; A.at(2*i+1,2) = 1;A.at(2*i+1,3) = 0.0; A.at(2*i+1,4) = 0.0;
A.at(2*i+1,5) = 0.0;A.at(2*i+1,6) = -u2*u1; A.at(2*i+1,7) = -u2*v1; A.at(2*i+1,8) = -u2;
}
// 定义输出变量,u是左边的正交矩阵U, w为奇异矩阵,vt中的t表示是右正交矩阵V的转置
cv::Mat u,w,vt;
//使用opencv提供的进行奇异值分解的函数
cv::SVDecomp(A, //输入,待进行奇异值分解的矩阵
w, //输出,奇异值矩阵
u, //输出,矩阵U
vt, //输出,矩阵V^T
cv::SVD::MODIFY_A | //输入,MODIFY_A是指允许计算函数可以修改待分解的矩阵,官方文档上说这样可以加快计算速度、节省内存
cv::SVD::FULL_UV); //FULL_UV=把U和VT补充成单位正交方阵
// 返回最小奇异值所对应的右奇异向量
// 注意前面说的是右奇异值矩阵的最后一列,但是在这里因为是vt,转置后了,所以是行;由于A有9列数据,故最后一列的下标为8
return vt.row(8).reshape(0, //转换后的通道数,这里设置为0表示是与前面相同
3); //转换后的行数,对应V的最后一列
}
H和F矩阵的区别
基础矩阵
基础矩阵:基础矩阵是对极约束的表示形式,对极约束中同时包含了平移和旋转。
F = K − T E K − 1 = K − T t ∧ R K − 1 \mathbf{F} = \mathbf{K}^{- T}\mathbf{E}\mathbf{K}^{- 1} = \mathbf{K}^{- T}\mathbf{t}^{\land}\mathbf{R}\mathbf{K}^{- 1} F=K−TEK−1=K−Tt∧RK−1
从上面的公式中可以看到,当平移 t \bold{t} t 为0时,基础矩阵 F \bold{F} F 也为0,从而导致根据 F \bold{F} F 来求旋转 R \bold{R} R 。此时可以通过单应矩阵来求。
基础矩阵的性质:
(1)基础矩阵 F \bold{F} F 是秩为2、自由度为7的齐次矩阵。
(2)若 p 1 \boldsymbol{p}_1 p1 与 p 2 \boldsymbol{p}_2 p2 是两幅图上的对应点,那么 p 2 T F p 1 = 0 \boldsymbol{p}_2^T \bold{F} \boldsymbol{p}_1 =0 p2TFp1=0 。
(3) l \boldsymbol{l} l 是对应于 p \boldsymbol{p} p 的对极线, l = F p \boldsymbol{l}= \bold{F} \boldsymbol{p} l=Fp 。
(4)若 e \boldsymbol{e} e 是第二个摄像机光心在第一幅图像上的极点,那么 F e = 0 \bold{F} \boldsymbol{e} =0 Fe=0 。
单应矩阵
单应矩阵:单应矩阵通常描述处于共同平面上的一些点在两张图像之间的变换关系。考虑在图像 I 1 I_1 I1 和 I 2 I_2 I2 有一对匹配好的特征点 p 1 \boldsymbol{p}_1 p1 与 p 2 \boldsymbol{p}_2 p2 。这些特征点落在平面 P 上,设这个平面满足方程: n T P + d = 0 \boldsymbol{n}^T \bold{P} + \boldsymbol{d}=0 nTP+d=0 ,整理得:
− n T P d = 1 -\frac{\mathbf{n}^{T}\mathbf{P}}{\mathbf{d}} = 1 −dnTP=1
前面说过的尺度意义下相等,得:
p 2 = K ( R P + t ) = K ( R P + t ⋅ ( − n T P d ) ) = K ( R − t n T d ) P = K ( R − t n T d ) K − 1 p 1 \mathbf{p}_{2} = \mathbf{K}\left( {\mathbf{R}\mathbf{P} + \mathbf{t}} \right) \\ = \mathbf{K}\left( {\mathbf{R}\mathbf{P} + \mathbf{t} \cdot \left( {- \frac{\mathbf{n}^{T}\mathbf{P}}{d}} \right)} \right) \\ = \mathbf{K}\left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{d}} \right)\mathbf{P} \\ = \mathbf{K}\left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{d}} \right)\mathbf{K}^{- 1}\mathbf{p}_{1} p2=K(RP+t)=K(RP+t⋅(−dnTP))=K(R−dtnT)P=K(R−dtnT)K−1p1
得到了一个直接描述图像坐标 p 1 \boldsymbol{p}_1 p1 与 p 2 \boldsymbol{p}_2 p2 之间的变换,把中间这部分记为 单应矩阵H:
H = ( R − t n T d ) \mathbf{H} = \left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{\mathbf{d}}} \right) H=(R−dtnT)
于是:
p 2 = H p 1 p_{2} = \mathbf{H}p_{1} p2=Hp1
它的定义与旋转、平移及平面的参数有关。
单应矩阵的性质:
- 自由度为8。
- 当相机进行纯旋转运动时,仍然可以求出R。
区别
F \bold{F} F 和 E \bold{E} E 的区别在于: F \bold{F} F 是像素点之间( p 1 \boldsymbol{p}_1 p1 与 p 2 \boldsymbol{p}_2 p2 )的对极约束, E \bold{E} E 是归一化坐标点之间( 和 )的对极约束。
根据 F \bold{F} F 的定义,只旋转不平移无法求解 F \bold{F} F ;根据 H \bold{H} H 的定义,只旋转不平移可以求解 H \bold{H} H 。
但仅有旋转,无法三角化求深度。
只旋转不平移能不能求F和H?
基础矩阵 F \bold{F} F 是根据对极约束来构造的,公式为:
F = K − T E K − 1 = K − T t ∧ R K − 1 \mathbf{F} = \mathbf{K}^{- T}\mathbf{E}\mathbf{K}^{- 1} = \mathbf{K}^{- T}\mathbf{t}^{\land}\mathbf{R}\mathbf{K}^{- 1} F=K−TEK−1=K−Tt∧RK−1
单应矩阵 H \bold{H} H 根据场景中的路标点处于同一个空间平面上来构造的,公式为:
H = ( R − t n T d ) \mathbf{H} = \left( {\mathbf{R} - \frac{\mathbf{t}\mathbf{n}^{T}}{\mathbf{d}}} \right) H=(R−dtnT)
本质矩阵 E \bold{E} E 同样是根据对极约束来构造的,公式为:
E = t ∧ R \mathbf{E} = \mathbf{t}^{\land}\mathbf{R} E=t∧R
F \bold{F} F 和 E \bold{E} E 的区别在于: F \bold{F} F 是像素点之间( p 1 \boldsymbol{p}_1 p1 与 p 2 \boldsymbol{p}_2 p2 )的对极约束, E \bold{E} E 是归一化坐标点之间( x 1 \boldsymbol{x}_1 x1 与 x 2 \boldsymbol{x}_2 x2 )的对极约束。
根据 F \bold{F} F 的定义,只旋转不平移无法求解 F \bold{F} F ;根据 H \bold{H} H 的定义,只旋转不平移可以求解 H \bold{H} H 。但仅有旋转,无法三角化求深度。
计算H矩阵和F矩阵的时候有什么技巧?
(实际上在问归一化的操作)。
因为要使用点构建A矩阵,求Ax=0。然后使用SVD分解求Ax=0的最小二乘解。在构建A矩阵前,首先对点进行标准化(均值为0,方差为1),这样可以增强数值稳定性。计算出F矩阵或H矩阵之后,再恢复尺度。
作者:深蓝学院 https://www.bilibili.com/read/cv7452301/ :
其中我能想到的技巧有两点,第一个是RANSAC操作,第二个是归一化操作,RANSAC操作前面已经解释过了,这里主要来分析下归一化操作,在《多视图几何》中提到了一种归一化八点法,方法是先用归一化矩阵对图像坐标进行平移和尺度缩放,然后利用八点法求解单应或者基础矩阵,最后再利用归一化矩阵恢复真实的单应或者基础矩阵,归一化具体操作和优势如下:
具体操作:又称各项同性缩放(非同性缩放有额外开销,但是效果并未提升),步骤如下
(1)对每幅图像中的坐标进行平移(每幅图像的平移不同)使点集的形心移至原点
(2)对坐标系进行缩放使得点x=(x,y,w)中的x,y,w总体上有一样的平均值,注意,对坐标方向,选择的是各向同性,也就是说一个点的x和y坐标等量缩放
(3)选择缩放因子使得点x到原点的平均距离等于
优势:
(1)提高了结果的精度;
(2)归一化步骤通过为测量数据选择有效的标准坐标系,预先消除了坐标变换的影响,使得八点法对于相似变换不变。
F矩阵退化会发生在哪些情况下?
F = K − T t ∧ R K − 1 p 2 T F p 1 = 0 \mathbf{F} = \mathbf{K}^{- T}\mathbf{t}^{\land}\mathbf{R}\mathbf{K}^{- 1} \\ \mathbf{p}_{2}^{T}\mathbf{F}\mathbf{p}_{1} = 0 F=K−Tt∧RK−1p2TFp1=0
则有:
p 2 T K − T t ∧ R K − 1 p 1 = 0 \mathbf{p}_{2}^{T}\mathbf{K}^{- T}\mathbf{t}^{\land}\mathbf{R}\mathbf{K}^{- 1}\mathbf{p}_{1} = 0 p2TK−Tt∧RK−1p1=0
原来的 F \bold{F} F 矩阵有7个自由度,什么情况下会发生 F \bold{F} F 矩阵的退化呢?
第一种情况:纯平移运动(就是沿着相机坐标系的z轴运动),这种情况下 E \bold{E} E 矩阵简化成了一个反对称矩阵 t ∧ \bold{t}^{\land} t∧ ,并且 t ∧ \bold{t}^{\land} t∧ 只有两个自由度(反对称矩阵并且尺度不变性),因此两组匹配点就可以求解这种情况。
第二种情况:纯平面运动(就是沿着相机坐标系的x轴运动),这种情况下 F \bold{F} F 矩阵的对称部分秩为2,所以会在原本的 F \bold{F} F 矩阵上再添加一个约束,使得自由度变成6个自由度。
第三种情况:标定之后的情形,其实就是 F \bold{F} F 矩阵在把内参获得之后就变成了 E \bold{E} E 矩阵,自由度变成五个自由度。
作者:深蓝学院 https://www.bilibili.com/read/cv7452301/ 出处:bilibili
相机在纯旋转下,单应矩阵和基础矩阵怎么应用,单目怎么做到初始化和三角测量
三角测量的公式推导及代码实现
VINS-Mono的方法
已知某个路标点 y \bold{y} y
y = [ X Y Z ] \mathbf{y} = \begin{bmatrix} X \\ Y \\ Z \\ \end{bmatrix} y=⎣ ⎡XYZ⎦ ⎤
在两帧的观测(归一化坐标)如下:
u 1 = [ u 1 v 1 1 ] , u 2 = [ u 2 v 2 1 ] \mathbf{u}_{1} = \begin{bmatrix}u_{1} \\v_{1} \\1 \\\end{bmatrix},~\mathbf{u}_{2} = \begin{bmatrix}u_{2} \\v_{2} \\1 \\\end{bmatrix} u1=⎣ ⎡u1v11⎦ ⎤, u2=⎣ ⎡u2v21⎦ ⎤
和世界坐标系到相机坐标系的矩阵(即位姿的逆) T 1 , T 2 \mathbf{T}_{1},\mathbf{T}_{2} T1,T2 ,则有:
λ 1 u 1 = T 1 y λ 2 u 2 = T 2 y \lambda_{1}\mathbf{u}_{1} = \mathbf{T}_{1}\mathbf{y} \\ \lambda_{2}\mathbf{u}_{2} = \mathbf{T}_{2}\mathbf{y} λ1u1=T1yλ2u2=T2y
对于 λ 1 u 1 = T 1 y \lambda_{1}\mathbf{u}_{1} = \mathbf{T}_{1}\mathbf{y} λ1u1=T1y 展开:
[ λ 1 u 1 λ 1 v 1 λ 1 ] = [ T 1 r o w 1 y T 1 r o w 2 y T 1 r o w 3 y ] \begin{bmatrix} {\lambda_{1}u_{1}} \\ {\lambda_{1}v_{1}} \\ \lambda_{1} \\ \end{bmatrix} = \begin{bmatrix} {{\mathbf{T}_{1}}_{row1}\mathbf{y}} \\ {{\mathbf{T}_{1}}_{row2}\mathbf{y}} \\ {{\mathbf{T}_{1}}_{row3}\mathbf{y}} \\ \end{bmatrix} ⎣ ⎡λ1u1λ1v1λ1⎦ ⎤=⎣ ⎡T1row1yT1row2yT1row3y⎦ ⎤
将第三行代入第1、2行,得:
T 1 r o w 3 y u 1 = T 1 r o w 1 y T 1 r o w 3 y v 1 = T 1 r o w 2 y {\mathbf{T}_{1}}_{row3}\mathbf{y}u_{1} = {\mathbf{T}_{1}}_{row1}\mathbf{y} \\{\mathbf{T}_{1}}_{row3}\mathbf{y}v_{1} = {\mathbf{T}_{1}}_{row2}\mathbf{y} T1row3yu1=T1row1yT1row3yv1=T1row2y
得:
( u 1 T 1 r o w 3 − T 1 r o w 1 ) y = 0 ( v 1 T 1 r o w 3 − T 1 r o w 2 ) y = 0 \left( {u_{1}{\mathbf{T}_{1}}_{row3} - {\mathbf{T}_{1}}_{row1}} \right)\mathbf{y} = 0 \\ \left( {v_{1}{\mathbf{T}_{1}}_{row3} - {\mathbf{T}_{1}}_{row2}} \right)\mathbf{y} = 0 (u1T1row3−T1row1)y=0(v1T1row3−T1row2)y=0
要求解的 y \bold{y} y 有3个未知数,因此至少三个方程。因此需要另一个点,有:
( u 2 T 2 r o w 3 − T 2 r o w 1 ) y = 0 ( v 2 T 2 r o w 3 − T 2 r o w 2 ) y = 0 \left( {u_{2}{\mathbf{T}_{2}}_{row3} - {\mathbf{T}_{2}}_{row1}} \right)\mathbf{y} = 0 \\ \left( {v_{2}{\mathbf{T}_{2}}_{row3} - {\mathbf{T}_{2}}_{row2}} \right)\mathbf{y} = 0 (u2T2row3−T2row1)y=0(v2T2row3−T2row2)y=0
合并上面四个方程,得:
[ u 1 T 1 r o w 3 − T 1 r o w 1 v 1 T 1 r o w 3 − T 1 r o w 2 u 2 T 2 r o w 3 − T 2 r o w 1 v 2 T 2 r o w 3 − T 2 r o w 2 ] y = D y = 0 \begin{bmatrix} {u_{1}{\mathbf{T}_{1}}_{row3} - {\mathbf{T}_{1}}_{row1}} \\ {v_{1}{\mathbf{T}_{1}}_{row3} - {\mathbf{T}_{1}}_{row2}} \\ {u_{2}{\mathbf{T}_{2}}_{row3} - {\mathbf{T}_{2}}_{row1}} \\ {v_{2}{\mathbf{T}_{2}}_{row3} - {\mathbf{T}_{2}}_{row2}} \\ \end{bmatrix}\mathbf{y} = \mathbf{D}\mathbf{y} = 0 ⎣ ⎡u1T1row3−T1row1v1T1row3−T1row2u2T2row3−T2row1v2T2row3−T2row2⎦ ⎤y=Dy=0
对D进行SVD分解,得:
D = U W V T \mathbf{D} = \mathbf{U}\mathbf{W}\mathbf{V}^{T} D=UWVT
得:
D V = U [ σ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ 0 ] \mathbf{D}\mathbf{V} = \mathbf{U}\begin{bmatrix} \sigma_{1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & 0 \\ \end{bmatrix} DV=U⎣ ⎡σ1⋮0⋯⋱⋯0⋮0⎦ ⎤
可知 V \bold{V} V 的最后一列满足 D V = 0 \bold{DV=0} DV=0 ,即 y = V c o l 4 \bold{y} = \bold{V}_{col4} y=Vcol4 。由于噪声影响, y \bold{y} y 的最后一行可能不唯一,因此需要进行归一化:
y = y ∥ y r o w 4 ∥ \mathbf{y} = \frac{\mathbf{y}}{\left\| \mathbf{y}_{row4} \right\|} y=∥yrow4∥y
代码
void GlobalSFM::triangulatePoint(Eigen::Matrix &Pose0, Eigen::Matrix &Pose1,Vector2d &point0, Vector2d &point1, Vector3d &point_3d)
{
Matrix4d design_matrix = Matrix4d::Zero();
design_matrix.row(0) = point0[0] * Pose0.row(2) - Pose0.row(0);
design_matrix.row(1) = point0[1] * Pose0.row(2) - Pose0.row(1);
design_matrix.row(2) = point1[0] * Pose1.row(2) - Pose1.row(0);
design_matrix.row(3) = point1[1] * Pose1.row(2) - Pose1.row(1);
Vector4d triangulated_point;
triangulated_point = design_matrix.jacobiSvd(Eigen::ComputeFullV).matrixV().rightCols<1>();
point_3d(0) = triangulated_point(0) / triangulated_point(3);
point_3d(1) = triangulated_point(1) / triangulated_point(3);
point_3d(2) = triangulated_point(2) / triangulated_point(3);
}
ORB-SLAM的方法
《计算机视觉的多视图几何》,241页
https://www.cnblogs.com/yepeichu/p/10792899.html
已知某个路标点 X \bold{X} X 在参考帧和当前帧的观测(像素坐标):
X = [ X Y Z ] , u r = [ u r v r 1 ] , u c = [ u c v c 1 ] \mathbf{X} = \begin{bmatrix} X \\ Y \\ Z \\ \end{bmatrix},\mathbf{u}_{r} = \begin{bmatrix} u_{r} \\ v_{r} \\ 1 \\ \end{bmatrix},~\mathbf{u}_{c} = \begin{bmatrix} u_{c} \\ v_{c} \\ 1 \\ \end{bmatrix} X=⎣ ⎡XYZ⎦ ⎤,ur=⎣ ⎡urvr1⎦ ⎤, uc=⎣ ⎡ucvc1⎦ ⎤
已知参考帧的位姿 T r w = [ R r w | t r w ] \mathbf{T}_{rw} = \left\lbrack \mathbf{R}_{rw} \middle| \mathbf{t}_{rw} \right\rbrack Trw=[Rrw∣trw] ,当前帧的位姿 T c w = [ R c w | t c w ] \mathbf{T}_{cw} = \left\lbrack \mathbf{R}_{cw} \middle| \mathbf{t}_{cw} \right\rbrack Tcw=[Rcw∣tcw] 。根据位姿和相机内参,可以构建参考帧和当前帧的投影矩阵 P r , P c \bold{P}_r,\bold{P}_c Pr,Pc ,且有:
u r = P r X u c = P c X \mathbf{u}_{r} = \mathbf{P}_{r}\mathbf{X} \\ \mathbf{u}_{c} = \mathbf{P}_{c}\mathbf{X} ur=PrXuc=PcX
可以将这两个投影方程展开为 A x = 0 \bold{Ax=0} Ax=0 的形式。
首先通过叉乘去掉齐次标量因子:
u r × P r X = u r × u r ⇒ u r × P r X = 0 \left. \mathbf{u}_{r} \times \mathbf{P}_{r}\mathbf{X} = \mathbf{u}_{r} \times \mathbf{u}_{r} \\ \Rightarrow\mathbf{u}_{r} \times \mathbf{P}_{r}\mathbf{X} = 0 \right. ur×PrX=ur×ur⇒ur×PrX=0
由于
u r ∧ = [ u r v r 1 ] ∧ = [ 0 − 1 v r 1 0 − u r − v r u r 0 ] P r = [ P r 1 T P r 2 T P r 3 T ] {\mathbf{u}_{r}}^{\land} = \begin{bmatrix} u_{r} \\ v_{r} \\ 1 \\ \end{bmatrix}^{\land} = \begin{bmatrix} 0 & {- 1} & v_{r} \\ 1 & 0 & {- u_{r}} \\ {- v_{r}} & u_{r} & 0 \\ \end{bmatrix} \\ \mathbf{P}_{r} = \begin{bmatrix} \mathbf{P}_{r}^{1T} \\ \mathbf{P}_{r}^{2T} \\ \mathbf{P}_{r}^{3T} \\ \end{bmatrix} ur∧=⎣ ⎡urvr1⎦ ⎤∧=⎣ ⎡01−vr−10urvr−ur0⎦ ⎤Pr=⎣ ⎡Pr1TPr2TPr3T⎦ ⎤
P r 1 T \mathbf{P}_{r}^{1T} Pr1T 表示 P r \mathbf{P}_{r} Pr 的第一行。则有:
u r × P r = [ 0 − 1 v r 1 0 − u r − v r u r 0 ] [ P r 1 T P r 2 T P r 3 T ] = [ v r P r 3 T − P r 2 T P r 1 T − u r P r 3 T u r P r 2 T − v r P r 1 T ] \mathbf{u}_{r} \times \mathbf{P}_{r} = \begin{bmatrix} 0 & {- 1} & v_{r} \\ 1 & 0 & {- u_{r}} \\ {- v_{r}} & u_{r} & 0 \\ \end{bmatrix}\begin{bmatrix} \mathbf{P}_{r}^{1T} \\ \mathbf{P}_{r}^{2T} \\ \mathbf{P}_{r}^{3T} \\ \end{bmatrix} = \begin{bmatrix} {v_{r}\mathbf{P}_{r}^{3T} - \mathbf{P}_{r}^{2T}} \\ {\mathbf{P}_{r}^{1T} - u_{r}\mathbf{P}_{r}^{3T}} \\ {u_{r}\mathbf{P}_{r}^{2T} - v_{r}\mathbf{P}_{r}^{1T}} \\ \end{bmatrix} ur×Pr=⎣ ⎡01−vr−10urvr−ur0⎦ ⎤⎣ ⎡Pr1TPr2TPr3T⎦ ⎤=⎣ ⎡vrPr3T−Pr2TPr1T−urPr3TurPr2T−vrPr1T⎦ ⎤
因此:
u r × P r X = 0 ⇒ [ v r P r 3 T − P r 2 T P r 1 T − u r P r 3 T u r P r 2 T − v r P r 1 T ] X = 0 ⇒ A X = 0 \left. \mathbf{u}_{r} \times \mathbf{P}_{r}\mathbf{X} = 0 \\ \Rightarrow\begin{bmatrix} {v_{r}\mathbf{P}_{r}^{3T} - \mathbf{P}_{r}^{2T}} \\ {\mathbf{P}_{r}^{1T} - u_{r}\mathbf{P}_{r}^{3T}} \\ {u_{r}\mathbf{P}_{r}^{2T} - v_{r}\mathbf{P}_{r}^{1T}} \\ \end{bmatrix}\mathbf{X} = 0 \\ \Rightarrow\mathbf{A}\mathbf{X} = 0 \right. ur×PrX=0⇒⎣ ⎡vrPr3T−Pr2TPr1T−urPr3TurPr2T−vrPr1T⎦ ⎤X=0⇒AX=0
该式子只有两行是独立的,比如 − u ( 第 1 行 ) − v r ( 第 2 行 ) = ( 第 3 行 ) - u\left( {第1行} \right) - v_{r}\left( {第2行} \right) = \left( {第3行} \right) −u(第1行)−vr(第2行)=(第3行) 。因此
[ u r P r 3 T − P r 1 T v r P r 3 T − P r 2 T ] X = 0 \begin{bmatrix} {u_{r}\mathbf{P}_{r}^{3T} - \mathbf{P}_{r}^{1T}} \\ {v_{r}\mathbf{P}_{r}^{3T} - \mathbf{P}_{r}^{2T}} \\ \end{bmatrix}\mathbf{X} = 0 [urPr3T−Pr1TvrPr3T−Pr2T]X=0
由于还有当前帧,因此每个点对最终列得的线性方程为:
[ u r P r 3 T − P r 1 T v r P r 3 T − P r 2 T u c P c 3 T − P c 1 T v c P c 3 T − P c 2 T ] X = 0 \begin{bmatrix} {u_{r}\mathbf{P}_{r}^{3T} - \mathbf{P}_{r}^{1T}} \\ {v_{r}\mathbf{P}_{r}^{3T} - \mathbf{P}_{r}^{2T}} \\ {u_{c}\mathbf{P}_{c}^{3T} - \mathbf{P}_{c}^{1T}} \\ {v_{c}\mathbf{P}_{c}^{3T} - \mathbf{P}_{c}^{2T}} \\ \end{bmatrix}\mathbf{X} = 0 ⎣ ⎡urPr3T−Pr1TvrPr3T−Pr2TucPc3T−Pc1TvcPc3T−Pc2T⎦ ⎤X=0
这是一个超定方程,通过SVD求最小二乘解即可得到 X \bold{X} X 。
/**
\* 三角化
\* @param kp1
\* @param kp2
\* @param P1 投影矩阵P1
\* @param P2 投影矩阵P2
\* @param x3D 输出的3D点
*/
void Initializer::Triangulate(const cv::KeyPoint &kp1, const cv::KeyPoint &kp2, const cv::Mat &P1, const cv::Mat &P2, cv::Mat &x3D)
{
//构造A矩阵
cv::Mat A(4,4,CV_32F);
A.row(0) = kp1.pt.x*P1.row(2)-P1.row(0);
A.row(1) = kp1.pt.y*P1.row(2)-P1.row(1);
A.row(2) = kp2.pt.x*P2.row(2)-P2.row(0);
A.row(3) = kp2.pt.y*P2.row(2)-P2.row(1);
//SVD分解
cv::Mat u,w,vt;
cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);
//取最小二乘解
x3D = vt.row(3).t();
//归一化,由于噪声影响,使得齐次变量X=[x,y,z,1]^T最后一行可能不为1
x3D = x3D.rowRange(0,3)/x3D.at(3);
}
提高三角测量的精度
不确定性:
当平移很小时,像素上的不确定性将导致较大的深度不确定性。也就是说,如果特征点运动一个像素 δ x \delta x δx ,使得视线角变化了一个角度 δ θ \delta \theta δθ ,那么将测量到深度值有 δ d \delta d δd 的变化。从几何关系可以看到,当 t 较大时, δ d \delta d δd 将明显变小,这说明平移较大时,在同样的相机分辨率下,三角化测量将更精确。
提高精度的方法:
其一是提高特征点的提取精度,也就是提高图像分辨率——但这会导致图像变大,增加计算成本。
另一方式是使平移量增大。但是,这会导致图像的外观发生明显的变化,比如箱子原先被挡住的侧面显示出来,又比如反射光发生变化,等等。外观变化会使得特征提取与匹配变得困难。总而言之,再增大平移,会导致匹配失效;而平移太小,则三角化精度不够——这就是三角化的矛盾。
如果假设特征点服从高斯分布,并且不断地对它进行观测,在信息正确的情况下,我们就能够期望它的方差会不断减小乃至收敛。这就得到了一个滤波器,称为深度滤波器(Depth Filter)。
基础矩阵的应用:点到极线的距离是否小于阈值?
平面几何基础
平面上直线的齐次表示
平面上的一条直线用 a x + b y + c = 0 ax + by + c=0 ax+by+c=0 的方程表示, a , b , c a,b,c a,b,c 的不同表示不同的直线。因此一条直线也可以用向量 ( a , b , c ) T (a,b,c)^T (a,b,c)T 表示, 同时 ( a , b , c ) T (a,b,c)^T (a,b,c)T 和 k ( a , b , c ) T k(a,b,c)^T k(a,b,c)T 表示同一条直线。
平面上点到齐次表示 : ( x , y , 1 ) (x,y,1) (x,y,1)
点x在直线l上当且仅当 x T l = 0 \bold{x}^T \bold{l}=0 xTl=0
两直线的交点: x = l × l ′ \bold{x} = \bold{l} \times \bold{l}' x=l×l′
过两点的直线为: l = x × x ′ \bold{l} = \bold{x} \times \bold{x}' l=x×x′
点到直线的距离:
d = a x + b y + c x 2 + y 2 d = \frac{ax+by+c}{\sqrt{x^2 + y^2}} d=x2+y2ax+by+c
基础矩阵的性质
源代码
ORB-SLAM源代码:
/**
* @brief 用基础矩阵检查极线距离是否符合要求
*
* @param[in] kp1 KF1中特征点
* @param[in] kp2 KF2中特征点
* @param[in] F12 从KF2到KF1的基础矩阵
* @param[in] pKF2 关键帧KF2
* @return true
* @return false
*/
bool ORBmatcher::CheckDistEpipolarLine(const cv::KeyPoint &kp1,const cv::KeyPoint &kp2,const cv::Mat &F12,const KeyFrame* pKF2)
{
// Epipolar line in second image l2 = x1'F12 = [a b c]
// Step 1 求出kp1在pKF2上对应的极线
const float a = kp1.pt.x*F12.at(0,0)+kp1.pt.y*F12.at(1,0)+F12.at(2,0);
const float b = kp1.pt.x*F12.at(0,1)+kp1.pt.y*F12.at(1,1)+F12.at(2,1);
const float c = kp1.pt.x*F12.at(0,2)+kp1.pt.y*F12.at(1,2)+F12.at(2,2);
// Step 2 计算kp2特征点到极线l2的距离
// 极线l2:ax + by + c = 0, (u,v)到l2的距离为: |au+bv+c| / sqrt(a^2+b^2)
const float num = a*kp2.pt.x+b*kp2.pt.y+c; //分子
const float den = a*a+b*b;//分母
if(den==0)return false;
const float dsqr = num*num/den;// 距离的平方
// Step 3 判断误差是否满足条件。尺度越大,误差范围应该越大。
// 金字塔最底层一个像素就占一个像素,在倒数第二层,一个像素等于最底层1.2个像素(假设金字塔尺度为1.2),3.84 是自由度为1时,服从高斯分布的一个平方项(也就是这里的误差)小于一个像素,这件事发生概率超过95%时的概率 (卡方分布)
return dsqr < 3.84*pKF2->mvLevelSigma2[kp2.octave];
}
RGB-D的SLAM和RGB的SLAM有什么区别?
(1)RGB-D相机优势之一不需要计算直接获得深度信息,双目RGB也可以获得深度但是需要根据视差进行计算;单目RGB的深度信息需要在估计出运动后通过三角化得到,但是随着相机运动会造成尺度漂移,需要通过回环检测进行纠正。
(2)RGB-D可以得到稠密地图,可以用于三维重建,或者转为八叉树地图进行路径规划和导航;单目RGB只能得到稀疏特征点地图,用来定位。
(3)在跟踪过程中,有时会出现地图点越来越少的情况,对于RGB-D相机和双目相机来说可以很容易的恢复3D的MapPoints,帮助系统进行优化。
求解Ax=0
【代数之美】线性方程组Ax=0的求解方法
在3D视觉中,我们常常会遇到这样一个问题:求解线性方程组Ax=0,从矩阵映射的角度来说,所有解组成了矩阵A的零空间。一个典型的场景比如用八点法求解本质矩阵E。
对于 A x = 0 \bold{A} \bold{x}=0 Ax=0 ,很明显,x=0必然是其中一个解,但是对我们实际应用来说,得到一个零解往往没有什么意义,所以不做讨论。
如前所述,我们实际要得到的,是非零解 。
特解
介绍一下特解的概念。一个显而易见的点是, A x = 0 \bold{A} \bold{x}=0 Ax=0 是尺度不变的,即若 x s \bold{x}_s xs 是其中一个解,则 k s x s k_s \bold{x}_s ksxs 必然也是其解( k s k_s ks 是实数),而 k s x s k_s \bold{x}_s ksxs 和 x s \bold{x}_s xs 是线性相关的;再进一步,如果 x t \bold{x}_t xt 是另一个与 x s \bold{x}_s xs 线性无关的解,即:
A x s = 0 , A x t = 0 , x t 和 x s 线性无关 \bold{A} \bold{x}_s = 0,\bold{A} \bold{x}_t = 0, \bold{x}_t 和 \bold{x}_s 线性无关 Axs=0,Axt=0,xt和xs线性无关
则显然 A ( k s x s + k t x t ) = 0 \bold{A} (k_s \bold{x}_s + k_t \bold{x}_t) = 0 A(ksxs+ktxt)=0 也是成立的( k s k_s ks , k t k_t kt 是实数),即 k s x s + k t x t k_s \bold{x}_s + k_t \bold{x}_t ksxs+ktxt 也是方程的解。这揭示一个现象:如果方程组 A x = 0 \bold{A} \bold{x}=0 Ax=0 有若干个线性无关解 x 1 , x 2 , ⋯ , x n \bold{x}_1,\bold{x}_2,\cdots,\bold{x}_n x1,x2,⋯,xn ,则 x 1 , x 2 , ⋯ , x n \bold{x}_1,\bold{x}_2,\cdots,\bold{x}_n x1,x2,⋯,xn 的任意线性组合也是其解,换句话说,所有的解都可以通过 x 1 , x 2 , ⋯ , x n \bold{x}_1,\bold{x}_2,\cdots,\bold{x}_n x1,x2,⋯,xn 来线性组合。 我们便把这些线性无关解 x 1 , x 2 , ⋯ , x n \bold{x}_1,\bold{x}_2,\cdots,\bold{x}_n x1,x2,⋯,xn 称为方程组 A x = 0 \bold{A} \bold{x}=0 Ax=0 的特解。
所以,我们的目的,实际上是要计算所有的非零特解。
有多少非零特解呢?
我们从消元回代解法来分析,假设一个矩阵 A ∈ R m × n \bold{A} \in \mathbb{R}^{m\times n} A∈Rm×n
A = [ 1 3 6 6 2 2 4 8 4 4 8 16 ] \bold{A} = \begin{bmatrix} 1&3&6&6 \\ 2 &2&4&8 \\ 4&4&8&16 \end{bmatrix} A=⎣ ⎡1243246486816⎦ ⎤
首先对 A \bold{A} A 进行消元:
[ 1 3 6 6 2 2 4 8 4 4 8 16 ] → [ 1 3 6 6 2 2 4 8 0 0 0 0 ] → [ 1 3 6 6 0 2 4 2 0 0 0 0 ] \begin{bmatrix} 1&3&6&6 \\ 2 &2&4&8 \\ 4&4&8&16 \end{bmatrix} \to \begin{bmatrix} 1&3&6&6 \\ 2 &2&4&8 \\ 0&0& 0 &0 \end{bmatrix} \to \begin{bmatrix} \boxed{1} &3&6&6 \\ 0 &\boxed{2}&4&2 \\ 0&0& 0 &0 \end{bmatrix} ⎣ ⎡1243246486816⎦ ⎤→⎣ ⎡120320640680⎦ ⎤→⎣ ⎡100320640620⎦ ⎤
消元后,将方框内的1和2称为主变量 (pivot variable) ,也称为主元。主元的个数称为矩阵的秩,因此上面矩阵的秩为2.
主元所在的列称为主列,(pivot column),这里的主列分别为第1列和第2列,其余列第3列和第4列为自由列(free column)。自由列中的变量为自由变量(free variable),自由变量的个数为:
n − rank ( A ) = 4 − 2 = 2 n-\text{rank}(\bold{A}) = 4 -2=2 n−rank(A)=4−2=2
按照消元解法,在消元后我们给自由变量赋值,回代去求主列变量的值。分别给自由变量 [ x 3 x 4 ] \begin{bmatrix}x_3 \\ x_4\end{bmatrix} [x3x4] 赋值为 [ 1 0 ] \begin{bmatrix}1 \\ 0\end{bmatrix} [10] 和 [ 0 1 ] \begin{bmatrix}0 \\ 1\end{bmatrix} [01] ,回代方程得到以下两个解向量:
[ 0 − 2 1 0 ] , [ − 3 − 1 0 1 ] \begin{bmatrix}0 \\ -2 \\ 1 \\ 0\end{bmatrix}, \begin{bmatrix}-3 \\ -1 \\ 0 \\ 1\end{bmatrix} ⎣ ⎡0−210⎦ ⎤,⎣ ⎡−3−101⎦ ⎤
这两个解向量就是线性方程组 A x = 0 \bold{A} \bold{x}=0 Ax=0 的两个非零特解,其他解都可以通过这两个解来线性表达:
x = a [ 0 − 2 1 0 ] + b [ − 3 − 1 0 1 ] \bold{x} = \bold{a} \begin{bmatrix}0 \\ -2 \\ 1 \\ 0\end{bmatrix} + \bold{b} \begin{bmatrix}-3 \\ -1 \\ 0 \\ 1\end{bmatrix} x=a⎣ ⎡0−210⎦ ⎤+b⎣ ⎡−3−101⎦